기존 풀이
function solution(n){
let arr = [];
let count = 0;
for(k=2; k <= n; k++){//2~n까지의 수 k를 돌면서
arr = [];
for(i=2; i < k; i++){//2~k-1의 수 중
arr.push(i);
}
const isPrime = arr.every((el)=>{
//나누어떨어지는 수가 하나도 없으면 소수이므로 true 반환
return k % el !== 0;
})
if(isPrime)count++
//소수이면 count ++
}
let answer = count;
return answer;
//1~n중 소수의 갯수 반환
}그러나 오답! 특히 효율성 테스트는 모두 통과하지 못했다.
에라토스테네스의 체로 이 부분을 해결할 수 있었다.
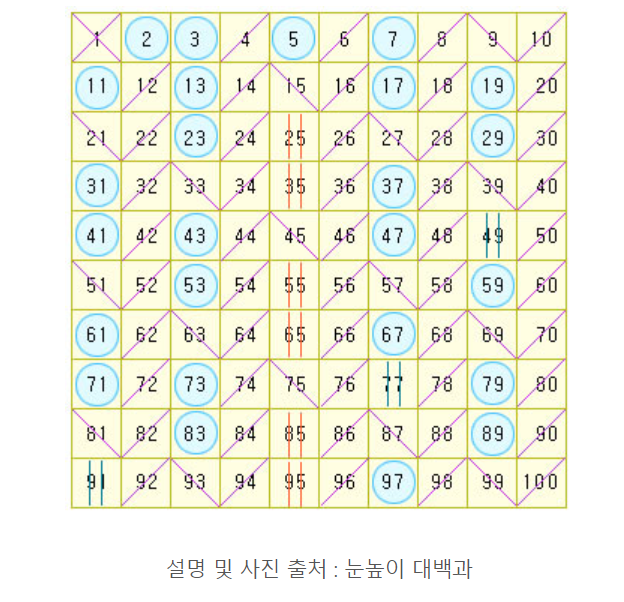
에라토스테네스의 체
1을 제외한 각 수의 배수를 모두 지워나가면, 소수만 남게 된다는 개념
function solution(n){
const nArr = new Array(n).fill(1)
nArr[0] = 0;
for(let i = 2; i*i <= n; i++){
for(let j = i*i; j <= n; j+=i){
nArr[j-1]=0;
}
}
return nArr.filter((el)=>el==1).length
}reference
Why?에서 시작해 How를 찾는 과정을 좋아합니다. 그 고민과 성장의 과정을 꾸준히 기록하고자 합니다.