[개발지식] 트리

1. 트리

계층적으로 데이터를 표현하기 위해 사용하는 자료구조

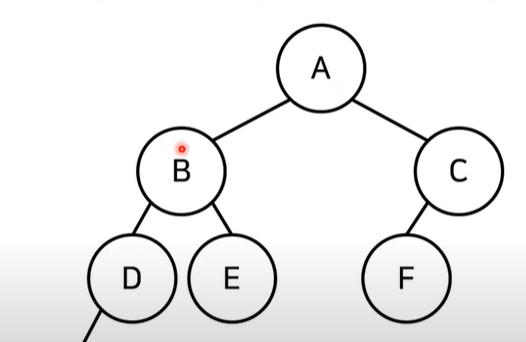
• 루트노드(parent node) : 부모가 없는 최상위 노드
• 단말노드(leaf node) : 자식이 없는 노드
• 크기(size) : 노드개수
• 루트노드로부터의 특정 노드까지의 거리(depth) : 깊이
• 깊이 중 최대값(height) : 높이

※ 트리크기가 N일때 간선개수는 N-1이다.

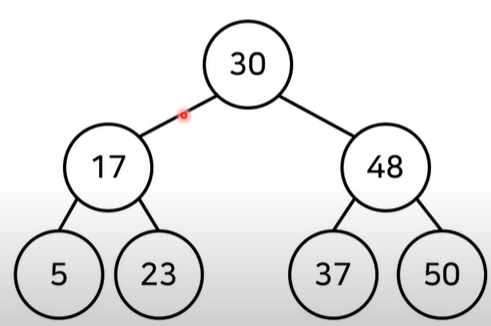
2. 이진탐색트리

Binary search tree, 이진탐색이 효과적으로 동작할 수 있도록 고안된 트리구조이다.

위와 같이 왼쪽자식<부모<오른쪽자식의 관계로 이루어져 있다.

3. 이진탐색트리에서의 데이터 조회

찾고자 하는 원소와 노드 원소를 서로 비교해가면서 순차적으로 탐색한다.

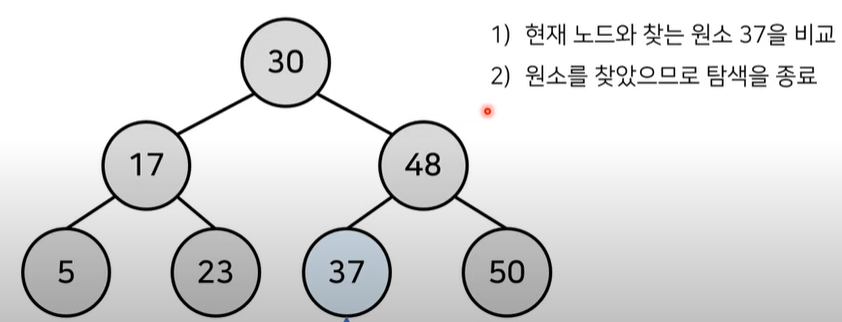
위 트리에서 37을 찾는다고 할때

• 루트노드에서 부터 방문하여 탐색진행, 최초 30보다 더 크므로 오른쪽 노드 방문
• 오른쪽 노드인 48과 비교하여, 왼쪽노드로 탐색 진행(더 작으므로)
• 37원소 탐색완료

4. 트리순회(Tree traversal)

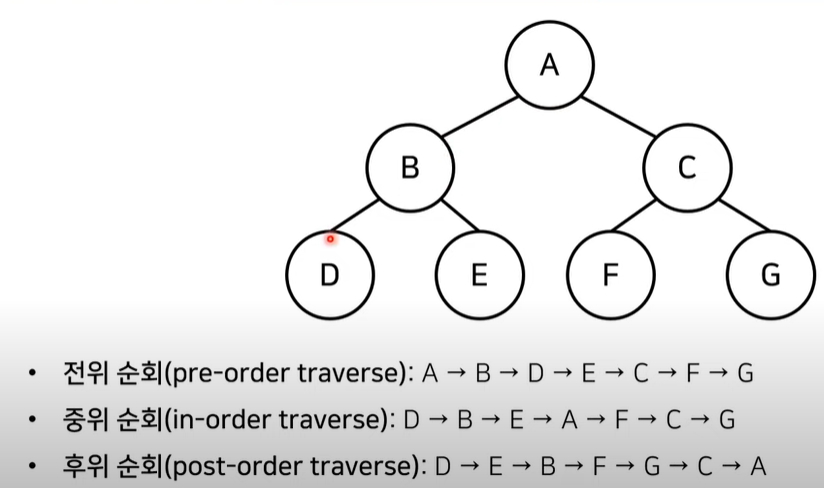
• 전위순회 : 루트를 먼저 방문하고, 그 후 왼쪽 오른쪽 노드 순으로 방문한다.
• 중위순회 : 왼쪽자식을 먼저 방문하고, 루트 오른쪽 노드 순으로 방문한다.
• 후위순회 : 왼쪽자식을 먼저 방문하고, 오른쪽 루트 순으로 방문한다.

5. 알고리즘 구현

유의사항

• class 구축하기
• print 순서에 유의하기

#트리순회

#class
#print 순서에 유의
class Node:
    def __init__(self, data, left_node, right_node):
        self.data = data
        self.left_node = left_node
        self.right_node = right_node

#전위 순회(root>left>right)
def pre_order(node):
    print(node.data, end=' ')
    if node.left_node != None:
        pre_order(tree[node.left_node])
    if node.right_node != None:
        pre_order(tree[node.right_node])

#중위 순회(left>root>right)
def in_order(node):
    if node.left_node != None:
        in_order(tree[node.left_node])
    print(node.data, end=' ')
    if node.right_node != None:
        in_order(tree[node.right_node])

#후위 순회(left>right>root)
def post_order(node):
    if node.left_node != None:
        post_order(tree[node.left_node])
    if node.right_node != None:
        post_order(tree[node.right_node])
    print(node.data, end=' ')

import sys
n = int(input())
tree = {}

for i in range(n):
    #node 개수 n개
    data, left_node, right_node = map(str, sys.stdin.readline().split())
    if left_node == "None":
        left_node = None
    if right_node == "None":
        right_node = None
    tree[data] = Node(data, left_node, right_node)

#결과출력
pre_order(tree['A'])
print()
in_order(tree['A'])
print()
post_order(tree['A'])

6. 참조자료

이코테 2021 - 이진트리/이진탐색
https://www.youtube.com/watch?v=i5yHkP1jQmo&list=PLRx0vPvlEmdAghTr5mXQxGpHjWqSz0dgC&index=12