Floating Point Number 는 부동소수점으로 Floating Ponit 를 Computer 에서는 어떻게 표현하는가? 에 대해 배우는 장이다.

Floating Pointer Register 는 32개로 Integer 와 동일하다는것을 알아야한다.

Floating Point

Pi= 3.141592,,,
e = 2.71828,,,
0.000000001= 1.0 10 의 -9 제곱
3155760000 =3.15576 10 의 9 제곱

이런 수를 어떻게 컴퓨터에서 표현하는지 배우는 것이다.

Scientific notation

Scientific notation 이란 1.0 10의 -9 제곱 처럼 소수점 왼쪽에 하나의 수만 만들어 주는것이다.
ex) 3.124 10 의 -9 제곱

근데 소수점 왼쪽의 범위는 1에서 9까지이다.
10 * 10의 2 제곱 이런거는 scientific notation 이 아니다.

Floating Point Number

컴퓨터는 소수점이 포함된 실수를 표현하기위해서 부동 소수점을 사용하는데, 강의내용에 적혀있는 부동소수점은 binary point 가 fix 되지 않는 수라고 한다. 나는 이 부분이 이해가 가지 않아서 인터넷을 찾아봤다.

소수점을 표현하기위해서는 고정 소수점(fixed point) 와 부동 소수점(floating point)를 사용하는데
고정 소수점은 소수점이 고정되었다는 뜻이라 한다.

32 비트에서 1비트를 부호 15비트를 정수 16비트를 소수점 이하의 자릿수를 표현한다해보자
9.6875는 양수임으로 0 정수는 9 임으로 000000000001001 소수점이하는 6875 임으로 1011000000000000 이라 할수있다.
그래서 00000000 00001001 10110000 00000000 이렇게 32bit 가 구성되게 된다.

이 고정 소수점 방식은 정수 부분과 소수 부분의 자리수가 적어서 표현할수 있는 범위가 적다고 한다.

부동 소수점은 이장의 파트임으로 뒤에서 더 배우도록 하겠다.

Floating Point Standard

두개의 표현 방식으로 나뉜다.
Single Precision, Double precision

일단 Precision 은 얼만큼 정밀하게 표현하는가를 나타내는 말이다.

Single precision 은 32비트 체계에서 사용하는 것으로
1 bit sign, 8 비트 exponent, 23 bit fraction 이다

Double precision 은 64 비트 체계에서 사용하는 것으로
1 bit sign, 11 bit exponent, 52 bit fraction 이다.

당연하게 64bit 체계에서 사용하는 Double precision 이 표현할수 있는 부동소수가 훨씬 클것이다.

Binary Representation

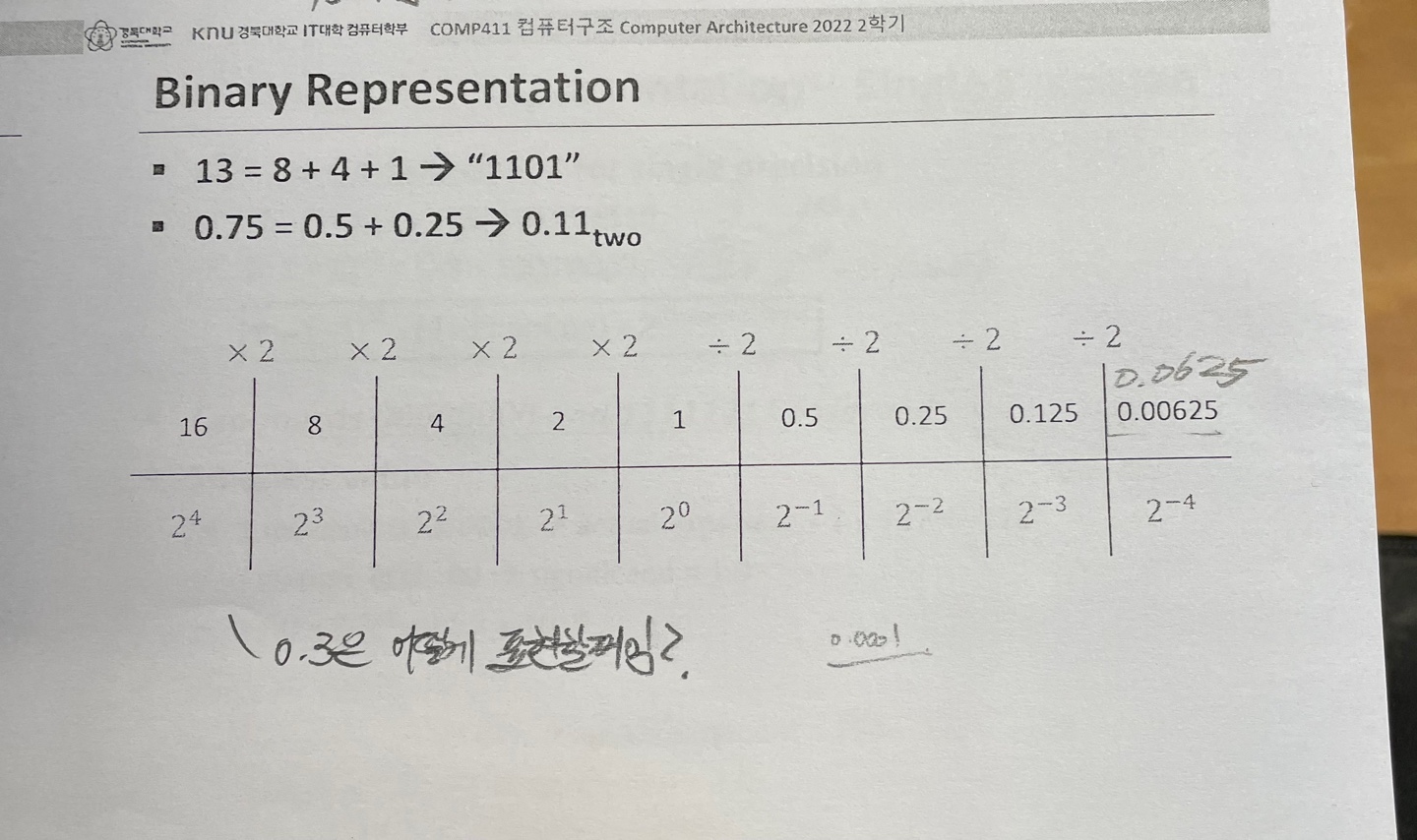
13은 1101
0.75는 0.11 이다.

Floating Point Representation

+- 1.xxxxxxx * 2의 yyyy 제곱으로 표현이 되는데
여기서 x 를 fraction, y를 exponent 라 한다.

exponent 는 표현할 수의 크기를 말하고 fraction은 얼마나 정밀하게 표현할수 있는가를 나타낸다.

위에서 말했던것처럼 32비트에는 23 개의 fraction 그리고 64bit에는 52개의 fraction 이 있다했다.
그래서 당연하게 double precision 이 더 정밀하게 표현할수 있게 된다.

significand 는 1+fraction 이라고 간단하게 설명하고 넘어가셨다.

그리고 표현할수 있는 수보다 크면 overflow 라고하고 표현할수 있는 수보다 작으면 underflow 라고 한다.

IEEE 754 floating point standard

exponent 가 11111111, fraction이 0 이면 Infinity 라는 수를 뜻하고
exponent 가 1에서 254 를 뜻하고, F 가 anything 이라면 normal FP number를 뜻한다.

Biased notation

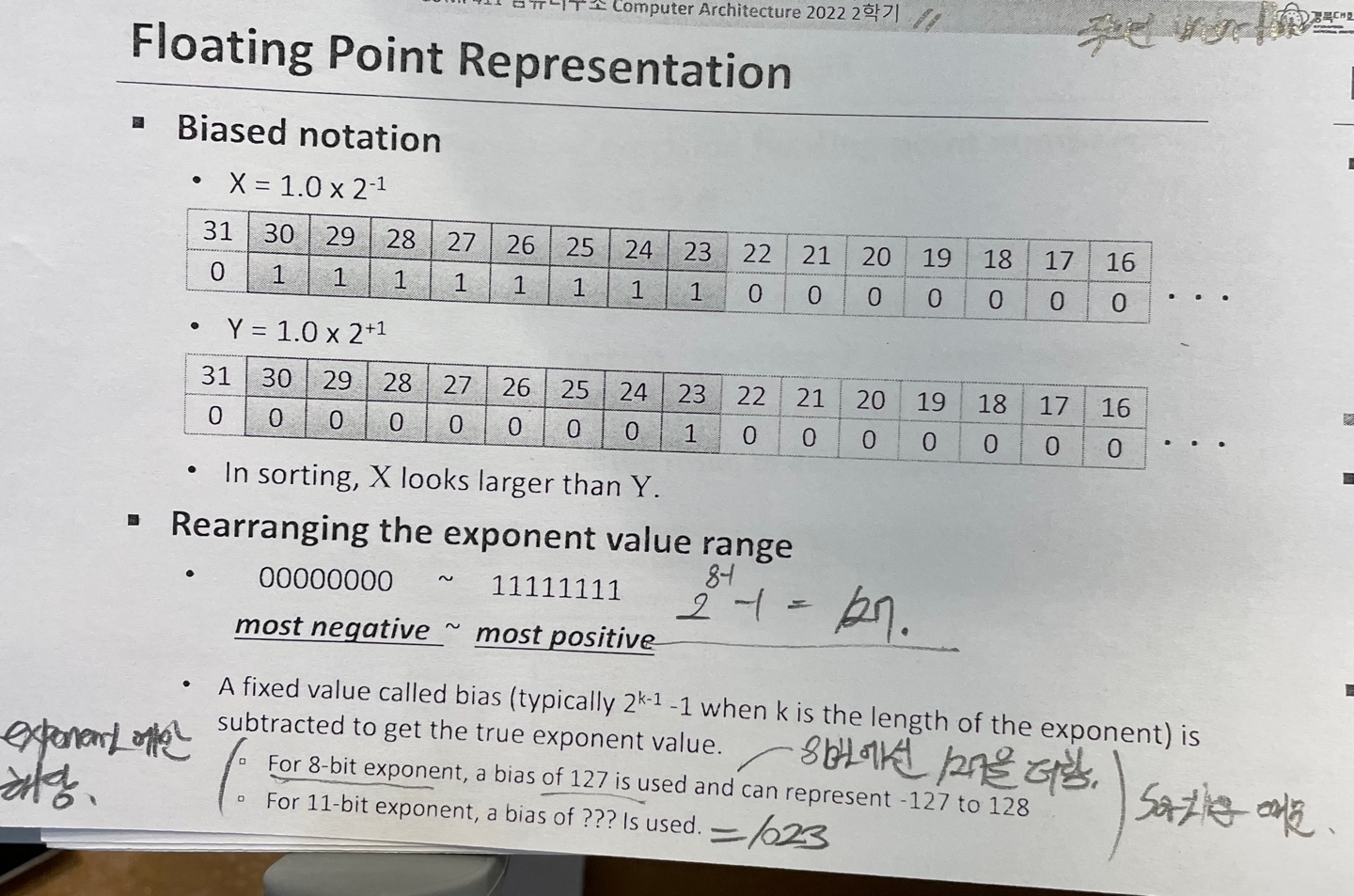
x 가 1.0 * 2 의 -1 제곱이라하면
exponent는 -1 인 11111111이 될것이고
fraction 은 00,,,,,이 될것이다.

x 가 1.0 * 2 의 1 제곱이라하면
exponent 는 1 인 00000001 이 될것이고
fraction 은 00,,,,,이 될것이다.

그리고 아까 표현할수있는 수의 크기를 exponent 라고 한다 했다.
32 bit 에서는 8비트를 가지고 있는데, 그러면 -128에서 127까지의 수를 표현할수 있을것이다.

그리고 exponent 부분에 sorting 을 위해 컴퓨터에 표현하기 위해선 exponent 에 127이라는 수를 더하는데 그러한건 뒤에서 조금더 설명하도록 하겠다.

Floating Point Representation - Single Precision

아까 exponent 에는 127을 더한다고 했다.
그러면은 만약 -1의 exponent 를 가지고 있다면 -1에서 127을 더한 126인
0111 1110 이라는 수가 표현되게 될것이고, 1 의 exponent 를 가지고 있다면 1 에서 127을 더한 128인 1000 0000 이라는 수가 표현될것이다.

X 는 (-1) 의 s 제곱 (1+Fraction) (2 의 (exponent-bias) 제곱) 이다.

Floating Point Representation - Double Precision

double precision 에는 64bit를 사용하며 exponent 는 11bit 이다.
11 bit 로는 -1024 ~ 1023 까지의 수를 표현할수 있다.

그래서 double precision 에는 1023의 수를 더해 exponent 를 표현한다.

IEEE 754 Floating Point Format

Floating Point Examples

Density Of Floating Point Numbers

32비트에서는 여전하게 2의 32 제곱의 수를 표현할수 있다.
FP Number 는 균등하게 저장되이어 있지 않다.

큰 수는 작은수보다 더 크게 저장되어있다.