Java 자료구조 - 힙 (Heap)

힙(Heap)

• 완전 이진 트리 형태로 중복 값을 허용한다.
• 최소값 또는 최대값을 빠르게 찾아내는데 유용한 자료구조
• 부모 노드는 자식노드보다 항상 우선순위가 높다.
• 형제 노드간 우선순위는 고려되지 않는다(반 정렬 상태)

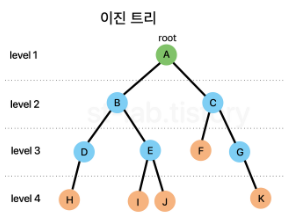
이진 트리(Binary Tree)

각 노드는 자식 노드를 최대 2개까지밖에 못갖는다.

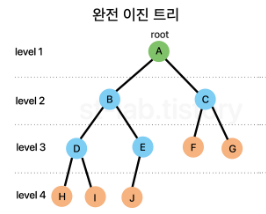
완전 이진 트리(complete binary tree)

'마지막 레벨'을 제외한 모든 노드가 채워져있으면서 모든 노드가 왼쪽부터 채워져있어야 한다.

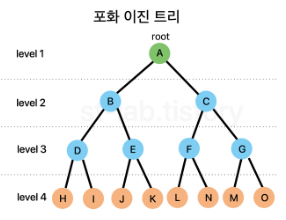
포화 이진 트리(perfect binary tree)

'마지막 레벨'을 제외한 모든 노드는 두 개의 자식노드를 갖는다.

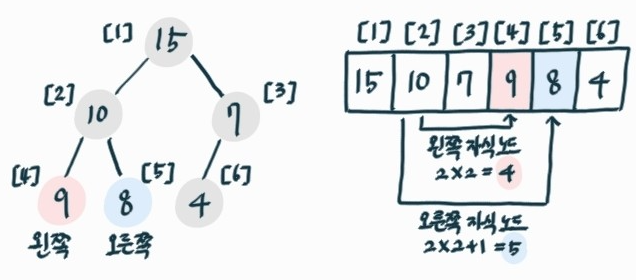
힙 구현

• 배열로 구현
• 인덱스 0을 사용하지 않음
• 부모 자식 사이 인덱스 관계
  • 인덱스 i에서 부모 인덱스 : i/2
  • 인덱스 i에서 왼쪽 인덱스 : i*2
  • 인덱스 i에서 오른쪽 인덱스 : (i*2)+1
    

최소 힙(Min Heap)

부모 노드의 키가 자식 노드의 키보다 작거나 같은 형태
형제 노드에서는 어느쪽이 커도 상관없음(반 정렬)

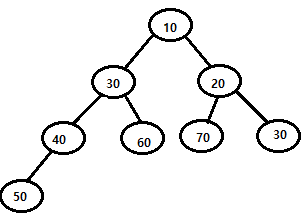
최대 힙(Max Heap)

부모 노드의 키가 자식 노드의 키보다 크거나 같은 형태

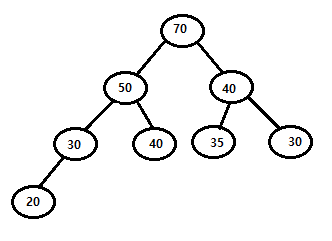
최소 힙 - 삽입

• 트리의 가장 끝 위치에 데이터 삽입
• 부모 노드와 키 비교한 후 작을 경우 부모 자리와 교체(반복)

최소 힙 - 삭제

• 최상위 노드 반환 및 삭제
• 가장 마지막 위치의 노드를 최상위 노드로 위치 시킴
• 자식 노드 중 작은 값과 비교 후 부모 노드가 더 크면 자리 교체(반복)

최대 힙의 경우 최소 힙과 반대

힙 시간복잡도

삽입 : O(log n)
삭제 : O(log n)
교환 : O(1)
두 연산 모두 최악의 경우 교환 횟수는 힙의 높이(height)가 된다. 힙은 완전 이진 트리이므로 높이가 log_2 n을 넘지 않는다. 따라서 두 연산의 시간복잡도는 O(log n)이다.