[Week2] Day7 경사하강법

📒 경사하강법(순한맛)

---

미분과 경사상승/하강법, 그래디언트 벡터에 관한 내용이었다.
dimension이 3이 넘어가는 순간부터는 이해하기가 너무 힘든 것 같다..
순한맛이 너무 매웠다. 강의를 두 번씩 돌려보면서 복습했다.

📝 미분

---

• 미분은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구이다.
• 최적화 단계에서 특히 많이 사용하는 기법이다.
• 변화율의 극한(limit)으로 정의한다.
  

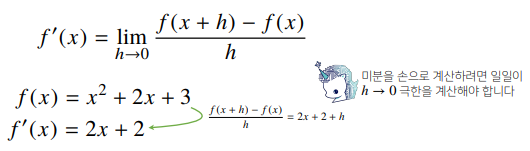
# 파이썬 sympy를 사용해서 미분을 구할 수 있다.
import sympy as sym
from sympy.abc import x

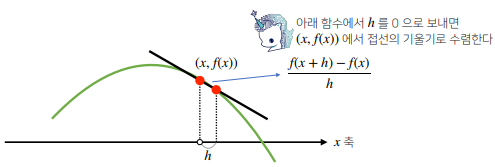
sym.diff(sym.poly(x**2 + 2 * x + 3), x)

• 미분은 함수 f의 주어진 점 (x, f(x)) 에서의 접선의 기울기를 구한다.
• 이 때, 미분을 계산하려면 함수의 모양이 매끄러워야(연속) 한다.
  

📝 경사 상승/하강법

---

• 한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야
  함수값이 증가/감소 하는지 알 수 있다.
• 미분값을 더하면 경사상승법(gradient ascent)라 하며,
  함수의 극대값의 위치를 구할 때 사용한다.
• 미분값을 빼면 경사하강법(gradient descent)라 하며,
  함수의 극소값의 위치를 구할 때 사용한다.
• 경사상승/경사하강 방법은 극값에 도달하면 움직임을 멈춘다.
  
  여기서 lr은 학습률로서, 미분을 통해 업데이트 하는 속도를 조절한다.
  종료조건이 성립하기 전까지 미분값을 계속 업데이트한다.

def func(val):
    fun = sym.ply(x ** 2 + 2 * x + 3)
    return fun.subs(x, val), fun
    
def func_gradient(fun, val):
    _, function = fun(val)
    diff = sum.diff(function, x)
    return diff.subs(x, val), diff

def gradient_descent(fun, init_point, lr_rate=13-2, epsilon=1e-5):
    cnt = 0
    val = init_point
    diff, _ = func_gradient(fun, init_point)
    while np.abs(diff) > epsilon:
        val = val - lr_rate * diff
        diff, _ = func_gradient(fun, val)
        cnt += 1
    print(f"함수 : {fun(val)[1]}, 연산횟수: {cnt}, 최소점 : ({val}, {fun(val)[0]})")
    
gradient_descent(func=func, init_point=np.random.uniform(-2,2))

📝 그레디언트 벡터

---

• 벡터가 입력인 다변수 함수인 경우 편미분을 사용한다.
  
  여기서 i번째 방향에서의 변화율을 계산할 수 있다.
• 각 변수 D개만큼 편미분을 계산한 것을 그레디언트(gradient) 벡터라고 한다.
• 그레디언트 벡터를 사용해서 경사하강/경사상승법에 사용할 수 있다
  
  

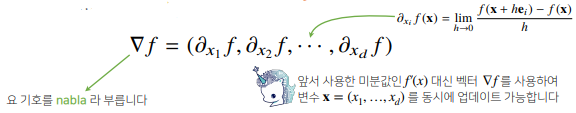
📒 경사하강법(매운맛)

---

복잡한 식이 많이 나왔지만, 머리로 이해만 하고 넘어가면 될 것 같다.
오랜만에 수학 공부를 해서 힘들지만 어떻게든 머리에 집어넣고 있다.
누구에게나 어려울 것이다. 열심히 공부하면 다 내 것이 될 것이다.

📝 선형회귀분석

---

• 선형 모델이 아닌 다른 방식의 모델을 사용할 때도 경사하강법을 이용해서 찾을 수 있다.
• 좀 더 일반적인 기계학습 모형에서 최적화 할때 역행렬이 아닌 경사하강법을 사용한다.
• 선형회귀의 목적식은 ||y-Xβ||₂ 이고, 이를 최소화하는 β를 찾아야한다.
  
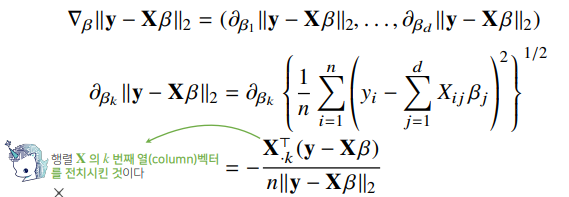
• 구현을 하기 위해서 직접 계산할 필요는 없지만, 식을 이해는 하고 넘어가자.
  
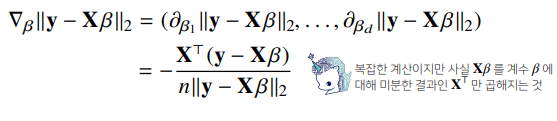
• 목적식을 최소화 하는 β를 구하는 경사하강법 알고리즘은 다음과 같다.
  
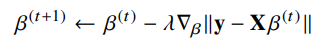
• L2 노름의 제곱을 최소화하면 식이 더 간단해진다.
  
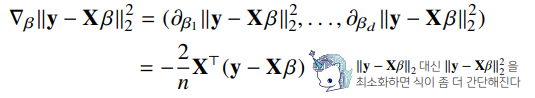
• 목적식을 최소화 하는 β를 구하는 경사하강법 알고리즘은 다음과 같다.
  

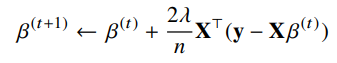
# Input: X, y, lr, T, Output: beta
# norm: L2-노름을 계산하는 함수
# lr: 학습률, T: 학습횟수
for t in range(T): # 종료 조건은 일정 학습횟수이다.
    error = y - X @ beta # y-Xβ와 동일한 식
    grad = -X.T @ error  # 그레디언트 벡터를 구함
    beta = beta - lr * grad # 위를 활용해서 β를 업데이트함.

✏️ 경사하강법은 만능일까?

• 이론적으로 경사하강법은 미분가능하고 볼록한 함수에 대해선
  적절한 학습률과 학습횟수를 선택했을 때 수렴이 보장되어 있다.
• 선형회귀의 경우 L2 노름을 활용한 목적식은 회귀계수 β에 대해
  볼록함수이기 때문에, 알고리즘을 충분히 돌리면 수렴이 보장된다.
• 비선형회귀 문제의 경우는 수렴이 항상 보장되지 않는다.

📝 확률적 경사하강법

---

• 확률적 경사하강법(SGD)은 모든 데이터를 사용해서 업데이트 하는 것이 아니라
  데이터를 한개 또는 일부를 활용하여 업데이트한다. (그레디언트 벡터)
  
• 볼록이 아닌 함수의 목적식을 SGD를 통해 최적화 할 수 있다.
• 데이터의 일부를 가지고 parameter를 업데이트하기 때문에 연산자원을 효율적으로 활용할 수 있다.
  
• 확률적으로 선택하는 미니배치를 가지고 그레디언트 벡터를 계산하므로 목적식 모양이 바뀐다.
• 일부 미니배치의 데이터로 업로드 및 업데이트가 가능하다.
  👉 빠른 연산이 가능하고 하드웨어의 한계를 극복하며 병렬 연산을 통해 딥러닝 학습이 가능하다.

📒 [퀴즈] 경사하강법- 1~5

---

5/5 Solve

📝 Q1

---

Q)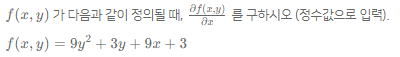

A) x로 미분 -> 9

📝 Q2

---

Q) 미분이 가능한 함수 f에 대해, 주어진 점 (x, f(x))에서의 접선의 기울기가 음수라면, x 를 증가시키면 함수값 f(x)이 증가한다.

A) 아니오 (감소한다.)

📝 Q3

---

Q) 다음 보기 중 함수의 극소값의 위치를 구할 때 사용하는 방법을 고르시오.

✔️경사하강법
  경사상승법
  오일러 급수
  SVM
  TSP

📝 Q4

---

Q) 경사하강법을 사용하여 구한 함수의 극소값의 위치는 해당 함수의 최소값의 위치가 아닐 수 있다.

A) 예 (최소값과 극소값은 다르다.)

📝 Q5

---

Q) 다음 보기 중 f(x, y, z)의 올바른 그래디언트 벡터를 고르시오.

f(x, y, z) = 9x² + 5y³ - 3z

  1. -(18x, 15y², -3)
  2. -(9, 5, -3)
✔️3. (18x, 15y², -3)
  4. (9, 5, -3)
  5. -(18x, 15y, -3)

(x로 미분, y로 미분, z로 미분)