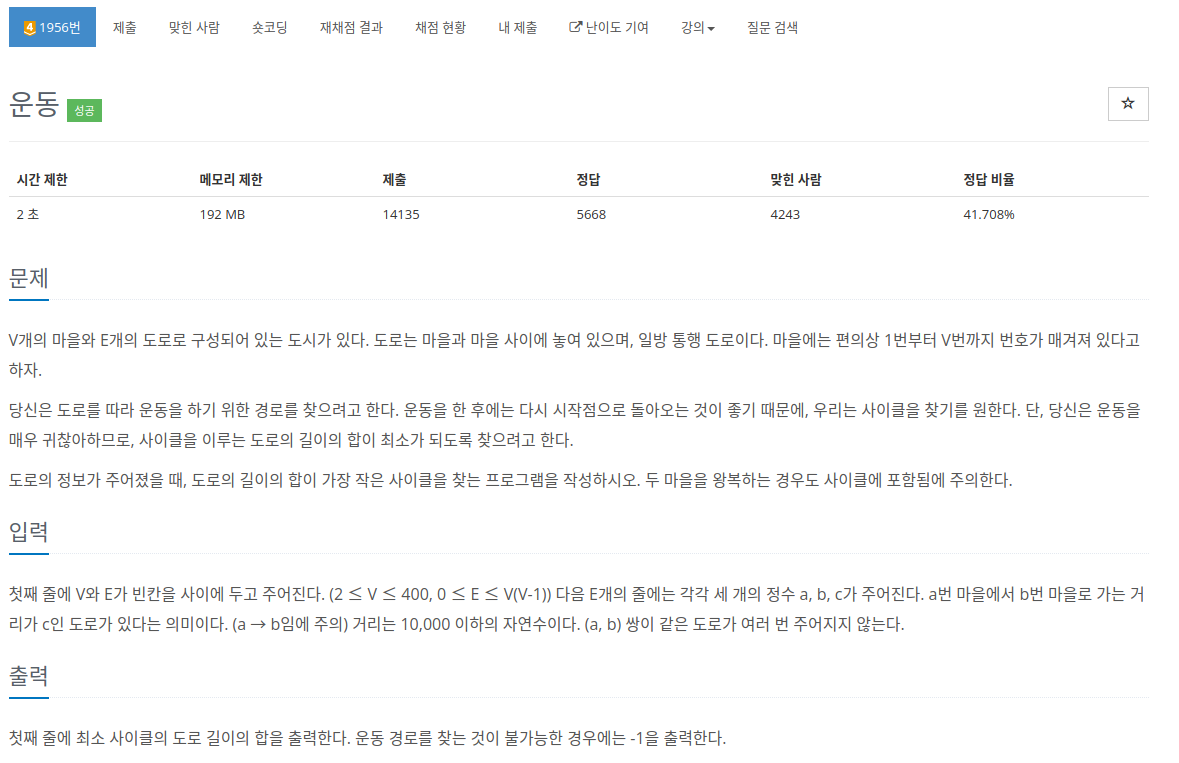
문제

!!!문제 링크!!!
https://www.acmicpc.net/problem/1956

풀이

간략히 문제를 설명하면....
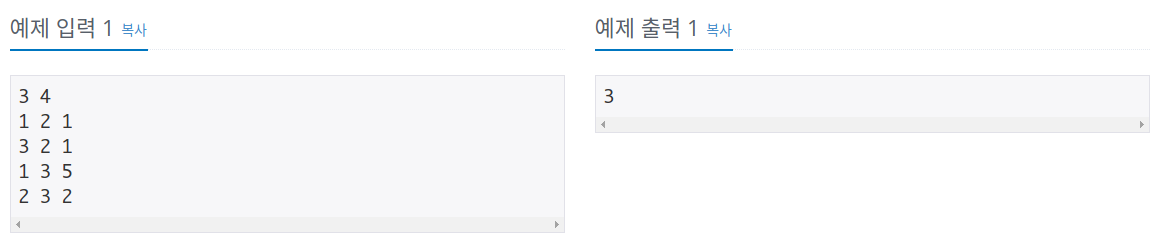
V개의 마을과 E개의 간선이 있는 마을이 있고 방향성이 있는 그래프이다.
한 마을쌍 (a,b)에는 도로가 최대 1개이다.
가능한 사이클 중 최소 사이클을 출력해주면 된다.

생각나는 방법으로는
다익스트라 알고리즘으로 1번 노드부터 V번노드까지 사이클을 전체 탐색후
제일 작은값을 출력해준다.

예를들어 step1부터 step N까지 있다하면
step K일 때는
K -> c -> K를 다익스트라로 비용을 구하고
(이때 c는 k를 제외한 모든 노드이다.)
모두 비교하고 그중 최솟값을 출력해주면 된다.

코드

import sys
import heapq

INF = int(1e9)
input = sys.stdin.readline

V, E = map(int, input().split())

graph = [[] for _ in range(V+1)]
all_distance = [[] for _ in range(V+1)]

for _ in range(E):
  a, b, c = map(int, input().split())
  graph[a].append((c, b))
#start노드에서 출발하여 갈수있는 최단경로 테이블을 리턴
def dijakstra(start):
  #리턴해줄 테이블 INF로 초기화
  distance = [INF] * (V+1)
  
  q = []
  heapq.heappush(q, (0, start))
  distance[start] = 0
  
  while q:
    dis, now = heapq.heappop(q)
    if(dis > distance[now]):
      continue
    for i in graph[now]:
      cost = dis + i[0]
      if(cost < distance[i[1]]):
        heapq.heappush(q, (cost, i[1]))
        distance[i[1]] = cost
  return distance
#모든 최단경로 테이블을 저장
for i in range(1, V+1):
  all_distance[i] = dijakstra(i)
#모든 가능한 사이클을 비교후 최솟값 변수 result에저장
result = INF
for i in range(1, V+1):
  for j in range(1, V+1):
    if(i != j):
      result = min(result, all_distance[i][j] + all_distance[j][i])
#사이클이 가능하지 않다면 -1출력 아니라면 최소사이클비용 출력
if(result < INF):
  print(result)
else:
  print(-1)

다른사람들의 코드를 보고난 후

어차피 모든 경로를 사용할 거면 플로이드 워셜을 사용할 수 있고
이때 코드가 더 단순하고 시간도 더 작게 걸렸다.

창의적인 방법을 또 찾을 수 있었는데
다익스트라 함수를 사용할때 테이블을 갱신하는 방법이아닌
heap에다가 갈수있는 경로를 계속 push하다보면 결국 사이클이 만들어질 수 있고
heap은 작은비용을 가지는 경로를 우선적으로 저장하므로 이때 처음 만들어지는 사이클을
출력하면 된다.
-> 두번째 방식은 꽤 신기하고 단순한 방법이었다.