문제

링크 https://www.acmicpc.net/problem/9370

풀이

요원들은 예술가 한쌍이 어디로가는지 알아내는 것이 임무이고 알고있는 정보로는
1. 그들이 s지점에서 출발한점
2. 목적지 후보들중 하나가 그들의 목적지라는점
3. 그들이 급하기때문에 최단거리로 간다는점
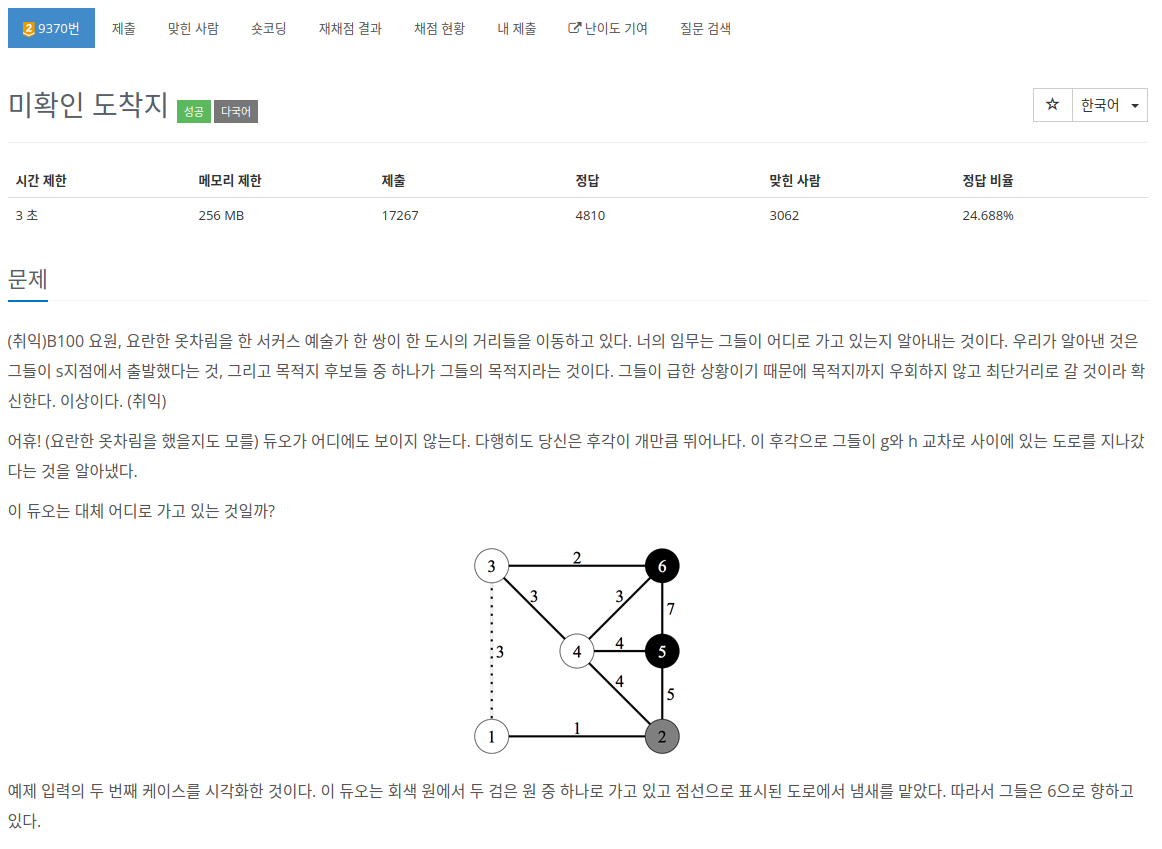
4. 후각으로 g와h사이의 도로를 지나갔다는 것을 알았다.
5. 또한 방향성이 없는 그래프이다.

프로그래밍 적으로 생각해보면.....
결국 목적지 후보들을 갈수있는 경우중 g - h사이의 도로를지날때 그경우가
최단경로이면 출력시키고 아니면 출력시키지 않는것이다.

따라서 간단히 해결방법을 생각해 볼 수 있는데 예시를 든다면
s에서 시작해 t개의 목적지를 갈때 s에서 h를 건너가는 경로의 비용을 먼저구한다,
(이때 t는 3이라하고 t(1), t(2), t(3)가 목적지후보 3개이다.)

t(n) 을 가는 경우의수 2가지의 경로가 나온다
s -> g -> h -> t(n)
s -> h -> g -> t(n)
이중 최단거리와 비용을 비교해야하므로 작은것 min값을 택한다.
min값과 dijakstra(s, min)을 비교해본다.
둘이 같다면 result 리스트에 목적지 후보를 저장하고
아니라면 저장하지않는다.

마지막으로 result리스트를 오름차순으로 정렬후 출력시킨다.

코드

import sys
import heapq

input = sys.stdin.readline
T = int(input().rstrip())
INF = int(1e9)

#매개변수로 받은 시작지점과 끝지점까지의 최단경로를 출력해주는 함수(다익스트라 알고리즘)
def dijakstra(start, end, size):
  distance = [INF] * (size+1) 
  #start노드부터 각 노드까지 최단경로를 저장하는 리스트
  
  q = []
  heapq.heappush(q, (0, start))
  distance[start] = 0
  
  while q:
    dis, cur = heapq.heappop(q)
    if (dis > distance[cur]):
      continue
    
    for i in graph[cur]:
      cost = dis + i[0]
      if cost < distance[i[1]]:
        heapq.heappush(q, (cost, i[1]))
        distance[i[1]] = cost
  
  return distance[end]

for _ in range(T):#테스트 케이스만큼 진행
  #결과를 저장하는 리스트
  result = []
  
  #각각 교차로, 도로 목적지후보들의 개수를 저장하는 변수
  n, m, t = map(int, input().split())
  s, g, h = map(int, input().split())
  
  graph = [[] for _ in range(n+1)]  
  min_distance = [INF] * (n+1)
  #m개의 도로의 정보 입력받기
  for _ in range(m):
    a, b, d = map(int, input().split())
    graph[a].append((d,b))
    graph[b].append((d,a))

  #t개의 목적지 후보 입력받기
  t_list = []
  for _ in range(t):
    t_list.append(int(input().rstrip()))
    
  
  #먼저 목적지 후보들의 최단경로를 min_distance리스트에 저장
  for i in t_list:
    min_distance[i] = dijakstra(s, i, n)

  #g-h거리 tmp에 저장
  for i in graph[g]:
    if i[1] == h:
      tmp = i[0]
  #목적지 후보들을 g-h도로를 건넜을때 최소비용을 구하고 최단경로와 비교
  for i in t_list:
    case1 = dijakstra(s, g, n) + tmp + dijakstra(h, i, n)
    case2 = dijakstra(s, h, n) + tmp + dijakstra(g, i, n)
    case = min(case1, case2)
    
    if(case == min_distance[i]):
      result.append(i)

  #오름차순으로 정렬 후 출력
  result.sort()
  for i in result:
    print(i, end = ' ')

  print()

다른사람의 코드를 보고난 후

나와 거의 비슷한 풀이로 풀었지만 dijakstra함수에서 차이가 났다.
나는 dijakstra함수를 시작점과 도착점을 매개변수로받아 그 경우의 최단거리를 출력했지만
다른 사람들은 distance리스트를 return해서 함수를 여러번 호출하지 않았다.
-> 이방식이 더 좋아보인다.

나와 다르고 창의적인 풀이가 있었는데 이 풀이는 dijakstra함수를 1번만 사용했다.
이 방식을 설명해보자면
g에서 h로가는 비용에 -0.1을 해주어서 기존 최단경로에 g에서 h로가는 경우를 포함한다면
최단경로가 float형으로나오고 아니라면 int형으로나와 dijakstra함수를 한번만 이용할 수 있는
창의적 코드도 있었다.

결론적으로는 나는 위의 코드가 다른사람이 봤을때 간결하고 가독성도 좋은것 같다.
하지만 밑에코드도 충분히 의미가 있고 창의적인 코드인것같다.