이.코.테 금광문제 파이썬

문제

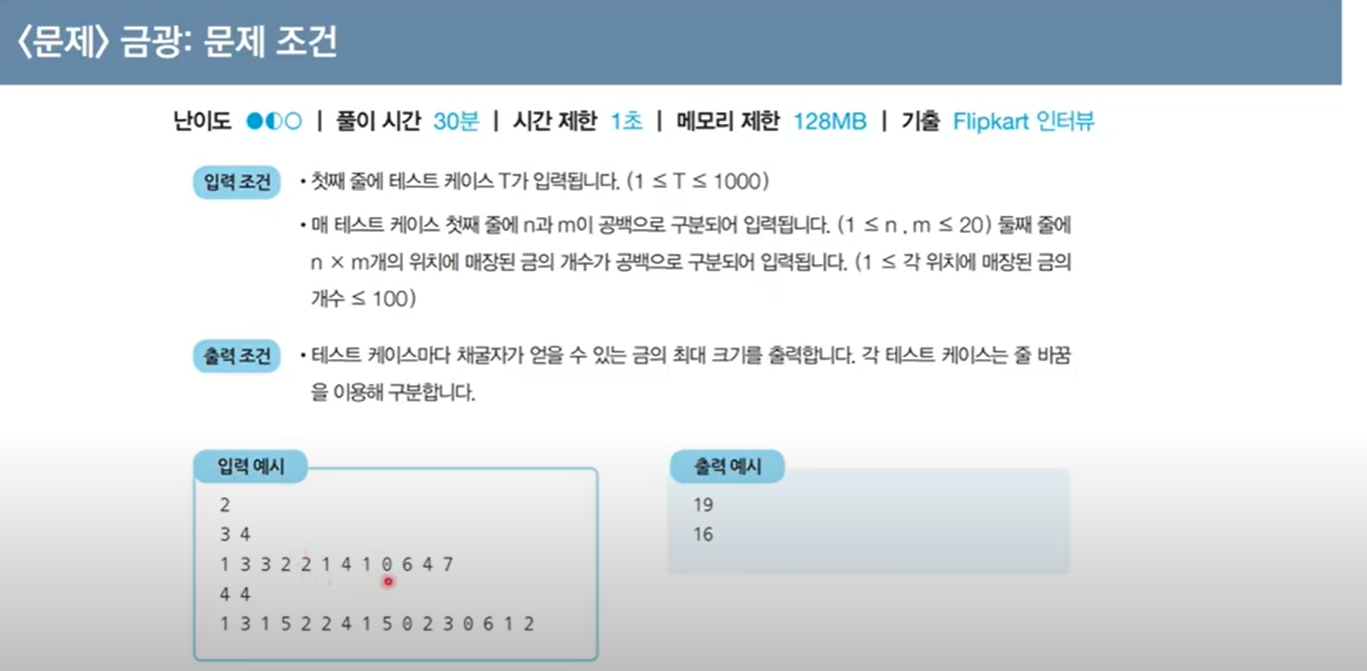
문제 해결방식

금광의 열의 좌표을 왼쪽에서부터 1이라 했을 때
dp 테이블을 이차원 배열로만들어준 뒤

첫째 이문제의 접근방식

1. 브루트포스 알고리즘으로 해결 할 수 있는가?

모든 경우의 수를 구해보려면
N부터 M까지를 순회하면서 모든 경로의 경우를 파악해야하므로
경우의 수는 최소 2의 M승 곱하기 N이 되므로 최대 연산을 고려해본다면

20 X 2 ^20이므로 1000 1000 20 = 200만을 훌쩍넘는 연산으로
시간제한 1초를 넘어갈 수 있다.

그렇다면 시간을 줄이는 방법은 뭐가 있을까?
2. 내가 배운방식중에는
자료구조이용하기, 이분탐색, dp가 있는데
이경우는 dp가 이용되기가 좋아보인다 왜냐하면

d[i][j]를 금광좌표 (i, j)까지 캘수있는 금광의 맥시멈값을 나타내는
dp테이블이라고 했을 때 d[i][j]와 d[i-1][j]들관의 연관성이 있는 점화식이
만들어진다.

이에따라 충분히 시간제한을 줄일 수 있다고 생각한다.

먼저 점화식을 표현해보자면 이렇다.
d[i][j] = matrix[i][j] + max(d[i-1][j], d[i-1][j-1], d[i-1][j+1])
인데

이 점화식을 활용해서 dp테이블을 바텀업 방식으로 채워간다면
모든 matrix만을 순회하는 정도의 연산횟수만이 작동되므로
시간복잡도는 O(n * m) -> max == 400정도로
시간제한에 걸리지 않는다.

따라서 구현만이 남았고
여기서 발생되는 문제점이 하나 있다.
문제의 조건에서는 1차원배열로 입력받아야하며
이때 점화식의 leftup, leftdown, left들을 받는데 2차원배열이 아니라
구현하기 까다롭다 먼저 이부분을 제외한 나머지를 구현해보자

구현방식으로는
빈공간의 2차원 리스트를 만들어 준 후 input_list를 2차원 리스트에 입력해주는 방식으로 구현하였다.

코드

#첫째줄에 테스트 케이스
#각 테스트케이스 마다 n, m 입력
#n과 m은 각각 행과 열을 의미
#행렬은 첫번째 행부터 1줄로 입력받음

#점화식 
#d[i][j] = matrix[i][j] + max(d[i-1][j], d[i-1][j-1], d[i-1][j+1]
import sys
T = int(input())

for k in range(T):
  n, m = map(int, sys.stdin.readline().split())

  #1차원 리스트로 입력받아서 matrix에 이차원 리스트로 만들어주기
  input_list = list(map(int, sys.stdin.readline().split()))

  count = 0
  matrix = []
  for i in range(n):
    tmp = []
    for j in range(m):
      tmp.append(input_list[count])
      count += 1
    matrix.append(tmp)

  
  dp = [[0] * m for _ in range(n)]

  #dp테이블 초기값 세팅
  for i in range(n):
    dp[i][0] = matrix[i][0]

  #dp테이블 작성
  for i in range(n):
    for j in range(1, m):
      if(i == 0):
        dp[i][j] = matrix[i][j] + max(dp[i][j-1], dp[i+1][j-1])

      elif(i== n-1):
        dp[i][j] = matrix[i][j] + max(dp[i][j-1], dp[i-1][j-1])
    
      else:
        dp[i][j] = matrix[i][j] + max(dp[i-1][j-1], dp[i][j-1], dp[i+1][j-1])

  result = -1
  for i in range(0, n):
    if(dp[i][m-1] > result):
      result = dp[i][m-1]

  print(result)