문제는 이렇다.

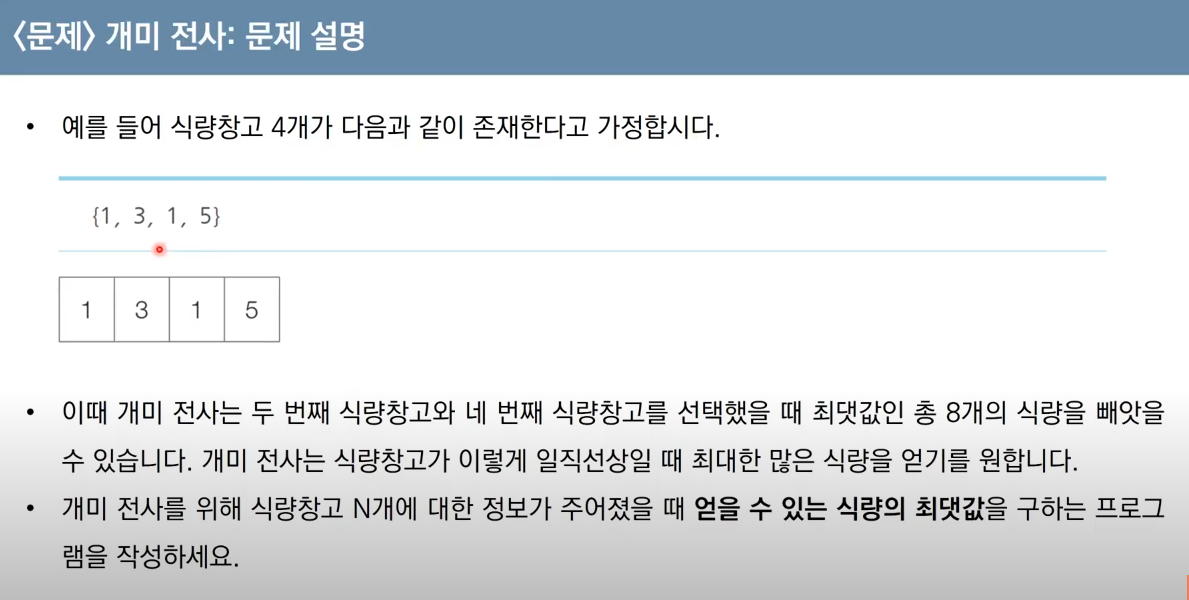
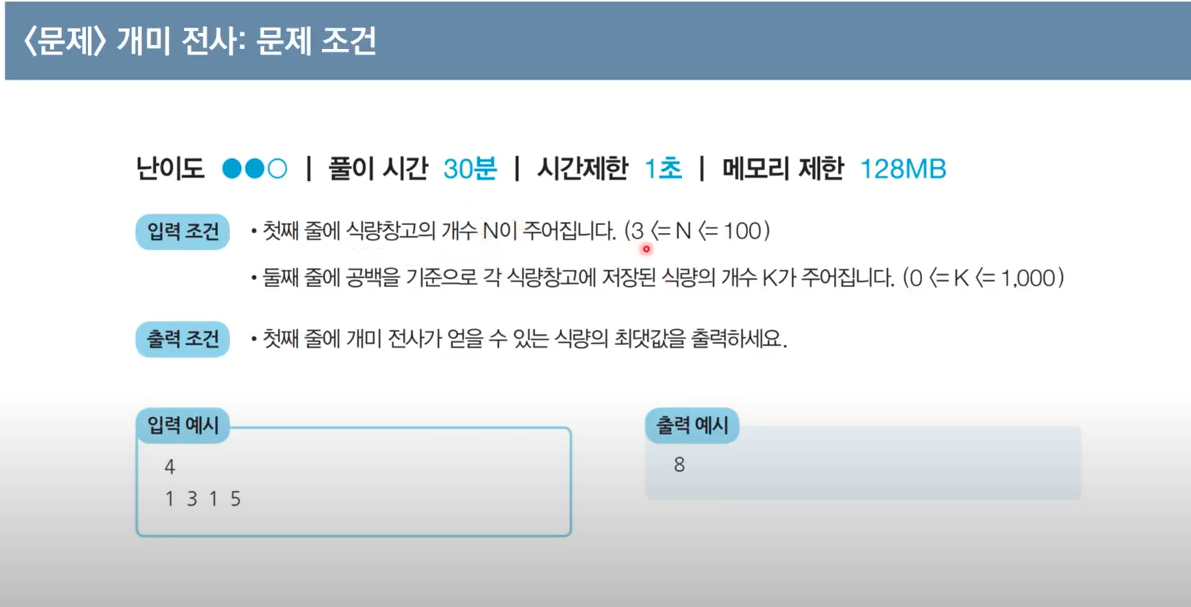
먼저 이문제를 처음봤다면 과연 dp로 풀 생각이 났을지는 모르겠지만, 만약 dp로 풀 수 있을려면
이문제의 조건이 dp의 조건을 만족하는지 확인해봐야 되었다.
먼저 이문제를 dp로 풀수있는지 확인해 보려면 i번째까지 식량창고에서 약탈할 수있는 최대양이 i-1이하의 최대양과 연관이 있는가? 라는 질문에서 시작해봐야한다.

고민해본결과

f(x)라은 함수를 x까지 식량창고의 약탈할 수 있는 최대양이라하면
f(x)는 x-1번째의 식량을 약탈했는지 확인해봐야 한다.

x-1번째를 약탈 했다면

f(x) == f(x-1)이고

x-1번째를 약탈 하지않았다면

f(x) == f(x- 2) + max(array[x-1], array[x])
일 것임이 분면하다.

이 두개의 근거를 고려해보면
접화식을 나타낼 수 잇는데

f(x) == f(x-2) + max(array[x-1]), array[X])

가 성립함을 알수있고, 따라서 이문제는 dp로 풀 수 있게된다!!!!!!

이를 기반으로 코드를 작성해본다면

#입력
#첫째줄 식량창고의 개수 N (3 <= N <= 100)
#둘째줄 N개의 각 식량창고의 식량의 양 K (0 <= K <= 1000)


#점화식
# f(i) = f(i-2) + max(array[i-1], array[i])일 것이다.
# f(1) = array[i]
# f(2) = max(array[1],  array[2])

import sys
import time
d = [0] * 1001

def food_max(flist, N):
  if(N == 1):
    d[1] = flist[0]
    return flist[0]
  if(N == 2):
    d[2] = max(flist[0], flist[1])
    return max(flist[0], flist[1])

  if d[N] != 0:
    return d[N]
  d[N] = food_max(flist, N-2) + max(flist[N-1], flist[N-2])
  return d[N]

N = int(input())

food_storage = list(map(int, sys.stdin.readline().split()))

start = time.time()
print(food_max(food_storage, N))

print('걸린시간 : ', time.time() - start)

이렇게된다.
따라서 이문제를 풀 수 있게된다. 이문제는 dp로 풀 수 있는지를 알아내면 편하게 풀 수 있는 문제이다.