Basic Probability

Factorial

n개를 나열하는 경우의 수
n개중 하나를 뽑고 그다음 n-1개에서 하나를 뽑고 반복
$n!=n\cdot(n-1)\cdots2\cdot1$
a,b,c를 나열하는 가지수는, abc, acb, bac, bca, cab, cba 총 6가지이다.

Permutation

$n$개 중에서 $k$개를 뽑고나서 $k$개를 나열하는 경우의 수
$a,b,c,d$에서 2개를 뽑는다면 $ab, ac,ad, ba, bc, bd, ca, cb, cd, da, db, dc$의 총 $4 \times 3=12$가지 경우의 수가 있다. 첫번째는 4개중 무엇이든 올수 있고 두번째는 첫번째 뽑힌 것이 제외된 것 3개 중에 뽑힐 수 있다. 뽑은 결과만을 본다면 $ab=ba, ac=ca, bc=cb, \cdots$와 같이 순서만 다른 중복된 경우를 가지고 있음을 알수있다. 그래서 k개를 뽑고 이것들을 나열하는 경우의 수까지 포함한다는 것을 알수 있다.
$_nP_k =n\cdot(n-1)\cdots(n-k+1) = \frac{n!}{(n-k)!}$
$_nP_k=\Pi_{i=1}^{k}(n-i-1)$
$_nP_n=n!$

Combination

$n$개 중에서 $k$개를 뽑는 경우의 수
permutation에서 중복된 결과를 하나로 묶는다(나눈다)고 볼수있다.
$_nC_k=\binom{n}{k}$
$_nP_k=_nC_k \cdot _kP_k$
$_nC_k=\frac{_nP_k}{_kP_k}=\frac{n!}{(n-k)!}\frac{1}{k!}$

Probability

전체 사건 중 특정 사건이 발생하는 비율이다.
어느 지역에서 U1대학에 다니는 학생의 출신 중학교와 고등학교를 조사했다. 단 3개의 중학교 M1,M2,M3만 존재했고 단 2개의 고등학교 H1,H2만 존재했다. 아래와 같은 발상이 가능하다.
전체사건: U1 대학생 중에서
특정사건: M1 중학교 졸업자 비율은?

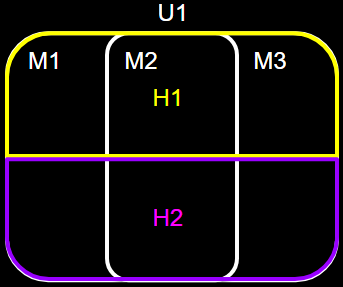
$n(U1)=100$
$n(M1)=25, \ n(M2)=35, \ n(M3)=40$
$n(H1)=40, \ n(H2)=60$
$n(M1 \cap H1)=10, \ n(M2 \cap H1)=20, \ n(M3 \cap H1)=10$
$n(M1 \cap H2)=15, \ n(M2 \cap H2)=15, \ n(M3 \cap H2)=30$
$P(U1)=1, \ P(M1)=\frac{n(M1)}{n(U1)}=0.25, \ P(M2)=0.35, \ P(M3)=0.4$
$P(H1)=0.4, \ P(H2)=0.6$

Joint Probability

결합확률은 교집합의 확률이다.
M2중학교를 졸업하고 H1고등학교를 졸업했을 확률
$P(M2,H1)=P(M2 \cap H1)$

Conditional Probability

조건부 확률은 Sample space를 전체 범위에서 특정 조건으로 좁혀진 후에 계산되어지는 확률이다.
H1고등학교를 졸업한 학생중에서 M2중학교를 졸업했을 확률은?
$P(M2|H1)=\frac{n(M2 \cap H1)}{n(H1)}=\frac{20}{40}=0.5$
$P(M2|H1)=\frac{P(M2 \cap H1)}{P(H1)}=\frac{\frac{20}{100}}{\frac{40}{100}}=0.5$
Sample space는 U1에서 H1으로 바뀐것이다.
조건부 확률은 내부 계산식에서 결합확률을 포함하고 있다.
$P(M2,H1)=P(M2 \cap H1)=P(M2|H1)P(H1)=P(H1|M2)P(M2)$

Marginal Probability

모든 중학교에서 H1고등학교로 간 학생
$P(H1)=\sum_{i=1}^3P(H1 \cap Mi)=\sum_{i=1}^3P(H1 | Mi)P(Mi)$
모든 고등학교에서 M1중학교를 졸업한 학생
$P()$

Disjoint Event

배반사건(함께 일어날수 없는 사건), Mutually Exclusive Events 라고도 한다.
M1, M2, M3는 동시에 일어날수 없기 때문에 서로 배반사건이다. 그리고 또한 H1, H2는 동시에 일어날수 없기 때문에 서로 배반사건이다. 중학교와 고등학교는 한곳씩만 졸업하기 때문이다. 존재할 수 없는 사건이기 때문에 무의미하지만 굳이 계산을 한다면 0이다.
$P(M1, M2)=0$

Independent Event

독립사건란 무엇일까?
$P(A,B)=P(A \cap B)=P(A)P(B)$ 이면 독립이다.
서로 관련이 없는 사건이다.
중학교를 졸업한 사건과 고등학교를 졸업한 사건은 독립일까?
$P(M1 \cap H1)=P(M1)P(H1)$
$\frac{10}{100} = \frac{25 \times 40}{10000}$
$P(M2 \cap H1)=P(M2)P(H1)$
$\frac{20}{100} \neq \frac{35 \times 40}{10000}$
$P(M3 \cap H1)=P(M3)P(H1)$
$\frac{10}{100} \neq \frac{40 \times 40}{10000}$
독립이 아니다.
중학교에서 고등학교로의 진학률 $P(H|M)$
고등학에서 중학교로부터의 입학률 $P(M|H)$
서로 진학률과 입학률 관계를 가지고 있다는 것은 중고등학교가 관련이 있다는 것이다.
만약에 중학교가 2개이고 고등학교가 2개라면, 그리고 정확히 반씩 교차로 나눠져서 입학했다면?
$P(M1 \cap H1)=P(M1)P(H1)$
$P(M2 \cap H1)=P(M2)P(H1)$
$P(M1 \cap H2)=P(M1)P(H2)$
$P(M2 \cap H2)=P(M1)P(H2)$
$\frac{25}{100} = \frac{50 \times 50}{100 \times 100}$
중학교를 졸업한 사건과 고등학교를 졸업한 사건은 독립이다.

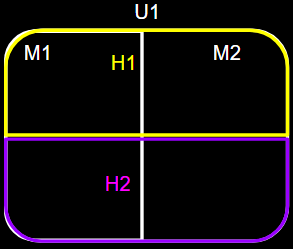
독립이다 = 관련이 없다 = 균등한 확률 관계이다 = 영향 없음
독립이 아니다 = 관련이 있다 = 비균등한 확률 관계이다 = 영향 있음

배반사건은 독립인가? 배반사건은 확률이 0이 나오기때문에 독립이 아니라고 볼수있지만 배반사건의 확률 자체가 무의미하기때문에 판단할 필요가 없다.

Bayesian theorem(rule)

베이지안 룰은 조건부확률의 변환이다.
$P(M1|H1)=\frac{P(H1 \cap M1)}{P(H1)}=\frac{P(H1|M1)P(M1)}{P(H1)}$
언제 유용할까?
H1 고등학교에 화재가나서 모든 학생들의 입학자료가 없어졌다.
P(H1)과 P(M1|H1)을 바로 알수 없다.
H1 고등학교 학생중 M1중학교에서 입학한 비율을 알아야한다면.
그래서 각 중학교에 자료를 요청해서 통계자료를 작성해야한다.
marginal probability를 이용해서 P(H1)을 구할수 있다.
$P(H1)={\sum_{i=1}^3P(H1|M_i)P(M_i)}$

$P(M1|H1)=\frac{P(H1|M1)P(M1)}{P(H1)}$
즉, 고등학교 자료 없이 중학교의 자료만으로 고등학교 입학률을 알수 있다. 직접적인 데이터 없이 관련된 데이터로 확률값을 계산 할 수 있게된것이다.

분류문제에 적용해 보자

H1고등학교기록이 없는 상태에서, 어느 학생이 H1고등학교을 졸업했다. 어느 중학교를 졸업했을 확률이 높을까?
$P(M1|H1)=\frac{P(H1|M1)P(M1)}{P(H1)}$
$P(M2|H1)=\frac{P(H1|M2)P(M2)}{P(H1)}$
$P(M3|H1)=\frac{P(H1|M3)P(M3)}{P(H1)}$
위 세가지 확률을 비교하면 된다.

남자여자 분류기

machine-learning 관점에서 본다면 feature로 부터 class를 예측하는 모델에 적용할 수있다.
class : 바로 알수 없는 알고 싶은 정보
feature: class와 관련이 있을거라고 생각되는 정보
$P(class_i|feature)=\frac{P(feature|class_i)P(class_i)}{P(feature)}$
남자증명사진과 여자증명사진을 모았다. 53%는 남자사진이고 47%는 여자사진이었다. 이는 남자여자의 인구 비율 10:9에 가까운 비율이었다.
$P(M)=0.53, \ P(F)=0.47$입을 알수 있고 확률이며 사전확률(prior probability)라고 한다.
모은 남자사진으로부터 n차원 HOG feature를 뽑아냈고 이 데이터로부터 GMM을 활용해 확률모델을 만들 수 있었다. $P(feature|M)$ 을 만들 수 있었다. 여자사진에도 같은 과적을 적용하여 $P(feature|F)$ 을 만들수 있었다. 남자 여자 두사진들을 모두 고려한 상황에서 $P(feature|M)P(M) + P(feature|F)P(F) \neq 1$ 이고 정확한 확률이라고 할 수는 없다. 하지만 어느정도 지표, 있을법하게 사용할 수있어서 $P(feature|class_i)$를 likelihood라고 한다. feature space가 class space와 일치하지 않기 때문이다. 즉, 강아지나 고양이의 feature는 남자도 여자도 아니기 때문이다.
이제 새로운 테스트 이미지가 들어왔고 남자인지 여자인지 분별하는 것은 비교이다.
$P(feature|M) \times P(M) < P(feature|F) \times P(F)$