논문 리뷰 : GraphSAGE(Inductive Representation Learning on Large Graphs)
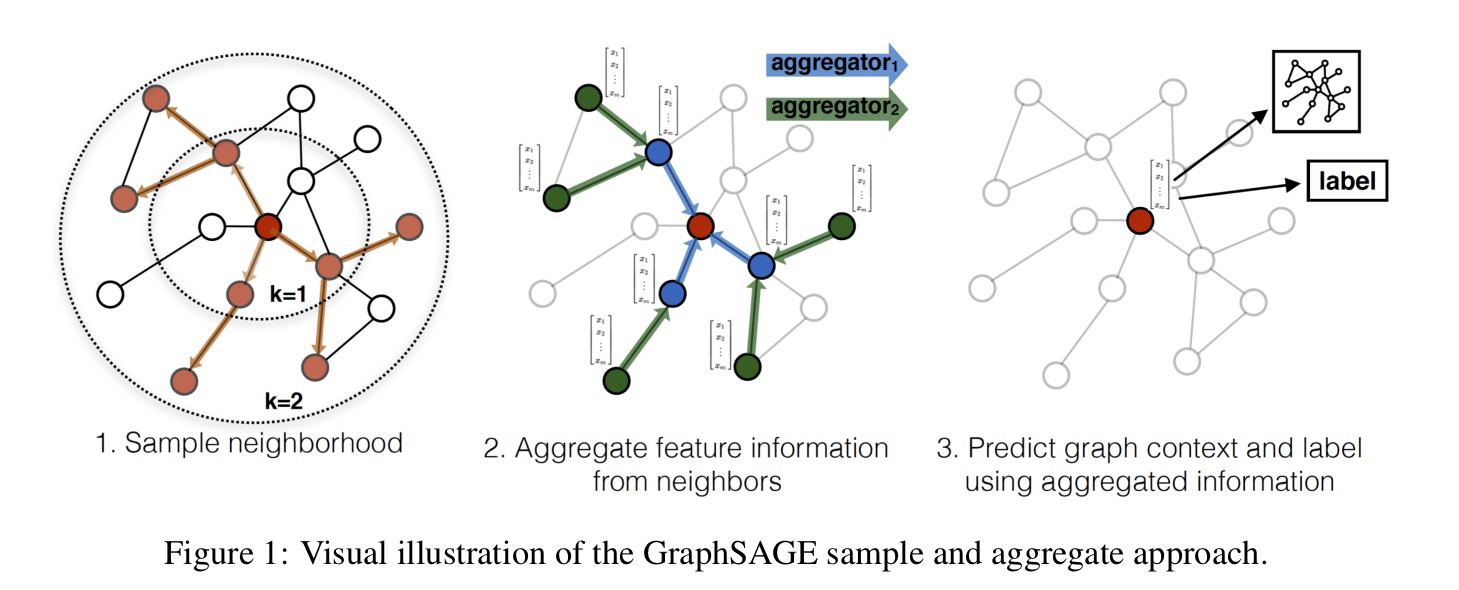
본 포스팅에서는 GraphSAGE 논문을 리뷰한다.
단순히 논문의 내용을 번역하는 데에 그치지 않으며 내용에 더한 추가 설명과 개념을 정리한다.
본문의 최하단에는 torch_geometric 로 구현한 코드를 정리한다.
포스팅 이해에 도움이 될 추가 자료
1. CS224W:GraphSAGE Neighbor Sampling
2. DSBA Paper Review MultiSAGE
- Graph Embedding 분야의 모델들을 추천시스템 분야에서도 사용할 수 있는 원리?
Graph Embedding 분야에서 제안된 모델들은 추천 시스템 분야에도 적용될 수 있다.
GraphSAGE와 GAT 같은 Graph Embedding 모델들은 Graph 데이터를 입력으로 받아 노드의 Embedding을 생성한다. Graph Embedding은 각 사용자와 아이템을 vector space에 Embedding한 것이다. 이 때, Graph 데이터에서 노드의 이웃 노드와의 관계를 학습하여, 이웃 노드들과의 상호작용을 고려한 Embedding을 생성할 수 있다. 추천 시스템에서sms 사용자와 아이템 사이의 상호작용을 Graph로 표현할 수 있으며, 이를 이용하여 사용자의 구매 이력, 아이템의 속성 등을 반영한 Embedding을 생성할 수 있다.
또한, 최근에는 Graph Embedding과 추천 시스템 모델을 결합하는 연구들도 많이 진행되고 있다. 예를 들어, Graph 신경망과 AutoEncoder 등을 결합하여, 추천 모델의 성능을 높이는 방법이 제안되고 있다. 이러한 연구들은 추천 시스템 분야에서 Graph 데이터를 활용하는 새로운 가능성을 제시하고 있다.
GraphSAGE의 트레이닝 프로세스 요약
GraphSAGE 모델의 학습 프로세스는 크게 두 가지 단계로 구성됩니다.
-
Supervised Learning
먼저, 각 노드에 대한 Ground Truth Label을 사용하여 모델의 임베딩 벡터를 학습시킵니다. 이 과정에서는 임베딩 벡터와 실제 레이블 간의 차이를 최소화하는 방향으로 학습이 이루어집니다. 이를 위해 일반적으로 cross-entropy loss나 mean squared error loss를 사용합니다. -
Unsupervised Learning
다음으로, 이웃 노드들을 사용하여 GraphSAGE 모델이 임베딩을 얻어내는 더 일반적인 방식인 unsupervised learning 단계가 진행됩니다. 이 단계에서는 모델이 노드 간의 상호작용을 고려하여 임베딩 벡터를 학습시킵니다.
-
각 노드 를 타겟 노드로 설정하고, 그 노드를 중심으로 k-hop 이웃 노드를 선택합니다.
-
선택한 k-hop 이웃 노드들의 임베딩 벡터를 Aggregation Function을 사용하여 하나의 벡터로 만듭니다.
-
만들어진 벡터와 타겟 노드의 임베딩 벡터를 Concatenate한 후, MLP를 통해 새로운 임베딩 벡터를 생성합니다.
-
이 과정을 모든 노드에 대해 반복하며, 모든 노드의 임베딩 벡터를 갱신합니다.
-
모든 노드의 임베딩 벡터가 갱신되면, 이를 다시 한 번 Supervised Learning 단계에서와 같은 방식으로 학습시킵니다. 이 과정에서도 Cross-entropy loss나 Mean Squared Error loss 등을 사용할 수 있습니다.
이와 같은 과정을 반복하면서, 모델은 점차적으로 노드 간의 상호작용을 파악하고, 이를 바탕으로 더욱 정교한 임베딩 벡터를 생성하게 됩니다.
아까 "선택한 k-hop 이웃 노드들의 임베딩 벡터를 Aggregation Function을 사용하여 하나의 벡터로 만듭니다." 라고 설명했었는데, 네가 여기서 말한 '하나의 벡터'는 노드 하나당 하나씩 생기는 거지?
네, 맞습니다. 하나의 노드에 대해서 선택한 k-hop 이웃 노드들의 임베딩 벡터를 Aggregation Function으로 합쳐서 하나의 새로운 임베딩 벡터를 생성합니다. 따라서 하나의 노드당 하나의 새로운 임베딩 벡터가 생성됩니다.
그렇게 만들어진 새로운 임베딩 벡터와, 그 노드의 정보가 담긴 임베딩 벡터를 Concatenate 하는 거야? 내가 이해한 게 맞아?
네, 맞습니다! Aggregation Function을 거쳐 만들어진 새로운 임베딩 벡터와 해당 노드의 정보가 담긴 임베딩 벡터를 Concatenate하여, 최종적으로 사용되는 임베딩 벡터를 만듭니다. 이렇게 만들어진 임베딩 벡터는 모델에서 다양한 downstream task를 수행하는 데 사용됩니다.
그러면 최종적으로 사용되는 임베딩 벡터의 개수는 샘플링된 전체 노드의 개수만큼 있겠네?
네, 맞습니다. 최종적으로 사용되는 임베딩 벡터의 개수는 K-hop 이웃 노드들을 샘플링한 전체 노드의 개수와 같습니다. 각 노드마다 이러한 과정을 거쳐 생성된 임베딩 벡터가 최종적으로 학습에 사용되는 것이죠.
1. Embedding Generation
Graph의 노드 각각에 대한 embedding을 직접 학습하게 되면, 새로운 노드가 추가되었을 때 그 새로운 노드에 대한 embedding을 추론할 수 없다. 따라서 GraphSage는, 노드 Embedding이 아닌 aggregation function을 학습하는 방법을 제안한다.
GraphSAGE에서는 target node의 이웃 노드 세트를 먼저 샘플링한 다음, 샘플링된 노드를 사용하여 feature vector의 aggregate를 계산하여 노드 Embedding을 학습한다. 이 Aggreation은 노드의 Embedding으로 사용되며, 분류 또는 회귀와 같은 머신러닝 작업에서 사용할 수 있다.
여기서 말하는 노드란 Neighborhood Representation의 Non-Linear Transformation이다.
실제 graph로 표현되는 데이터는 새로운 node들이 실시간으로 추가되는 경우(Evolving Graph)가 매우 많다. Evolving Graph의 경우, 한 서비스에서 신규 유저가 추가되었다면, 기존 유저+신규 유저에 대한 node representation을 처음부터 다시 학습해야 한다.
본 논문에서는 fixed graph에 대한 node embedding을 학습하는 transductive learning 방식의 한계점을 지적하고, evolving graph에서 새롭게 추가된 node에 대해서도 inductive node embedding을 산출할 수 있는 프레임워크인 GraphSage를 제안한다. 이름은 SAmple과 aggreGatE를 결합했다.
한편, inductive Node Embedding 문제는 어려운 편이다. 왜냐하면 지금껏 본 적이 없는 Node에 대해 일반화를 하는 것은 이미 알고리즘이 최적화한 Node Embedding에 대해 새롭게 관측된 subgraph를 맞추는 (align) 작업이 필요하기 때문이다. 따라서 inductive 프레임워크는 반드시 Node의 Graph 내에서의 지역적인 역할과 글로벌한 위치 모두를 정의할 수 있는 Node Neighborhood의 구조적인 특성을 학습해야 한다.
GraphSage는 행렬 분해에 기반한 Embedding 접근법과 달리, 아직 관측되지 않은 Node에 대해서도 일반화(generalization)가 가능한 Embedding 함수를 학습하기 위해 Node Feature(텍스트, Node 프로필 정보, Node degree 등)를 Leverage한다. 학습 알고리즘에 Node Feature를 통합함으로써, 논문에서는 이웃한 Node Feature의 분포와 각 Node의 이웃에 대한 위상적인 구조를 동시에 학습하는 방법을 제시한다. 풍부한 Feature를 가진 Graph에 집중한 접근법은 또한 (Node Degree와 같이) 모든 Graph에 존재하는 구조적인 Feature를 활용할 수 있다. 따라서 본 논문의 알고리즘은 Node Feature가 존재하지 않는 Graph에도 적용될 수 있다.
2. Neighborhood Sampling
노드의 embedding을 구하기 위해서는, 우선 거리(k)를 기준으로 일정 개수의 neighborhood node를 샘플링한다. 이때의 접근 방법은, 계산 복잡도를 제어하기 위해 각 iteration 마다 uniform random draw 방식으로 정해진 개수의 최근접 노드를 샘플링하는 것이다.
그렇다면 어떻게 특정 node u의 neighborhood N(u)를 정의할까?

- 한 노드에 대해 거리(k)를 기준으로 일정 개수의 neighborhood node를 샘플링할 때, 한 노드가 다른 노드의 K번쨰 이웃인지는 어떻게 판단하는가?
K-hop neighborhood는 해당 노드로부터 K번째 거리에 있는 모든 노드를 의미한다. 이것은 거리 기반 유사도를 사용하여 측정된다. 노드 간 거리를 계산할 때, 일반적으로는 가장 짧은 경로를 따라 계산하게 된다. 그리고 K-hop 이웃을 구할 때에는, 이 최단 경로에 따라서 해당 노드로부터 K번째에 위치한 모든 노드를 구하게 된다.
- 그럼 거리 기반 유사도 계산은, 한 노드의 feature 정보를 모두 고려해서 계산하는가?
보통은 한 노드의 feature 정보를 벡터로 표현하고, 이 벡터 간의 거리를 계산하여 거리 기반 유사도를 구한다. 이 때, 노드의 feature 정보는 Graph 구조와 관련된 정보와 함께 고려하여 계산할 수 있다. 예를 들어, 한 노드와 다른 노드 간의 거리를 계산할 때, 이들 간의 연결 관계와 노드 feature 정보를 모두 고려할 수 있다. 이러한 방식으로 계산된 거리 기반 유사도를 이용하여 K-hop 이웃을 샘플링하고, GraphSAGE에서 aggregator function을 이용하여 이웃 정보를 집계한다.
3. Aggregator Function
neighborhood node를 샘플링했다면, graphSAGE를 통해 학습된 aggregation function을 통해 주변 노드(이웃 노드)의 feature로부터 노드의 Embedding을 계산한다. 다시 말해 이 함수는 이웃 노드로부터 Feature Information을 통합한다.
한편 Weight Matrices의 집합은 모델의 다른 layer나 search depth 사이에서 정보를 전달하는데 사용된다.
Aggregation function은 인접한 노드들의 특징 벡터를 aggregate하여 target 노드의 새로운 특징 벡터를 생성한다. 이 과정에서 각 노드의 특징 벡터는 그 노드의 이웃 노드들의 정보를 참조하여 업데이트된다.
GraphSAGE에서 aggregator function은 각 노드의 이웃 노드들의 정보를 모아서 노드의 임베딩을 생성하는 역할을 합니다. 즉, 이웃 노드들의 특성을 집계해서 각 노드의 정보를 나타내는 벡터를 만드는 것입니다.
각 aggregator function은 특정 깊이(hop)에서 노드의 이웃 노드들로부터 정보를 수집합니다. 예를 들어, aggregator function이 2-hop aggregator인 경우, 노드의 이웃 노드와 이웃 노드의 이웃 노드들의 정보를 수집합니다. 이렇게 수집한 정보를 기반으로 노드의 임베딩 벡터를 계산합니다.
따라서, 각 노드의 임베딩은 그래프 내의 이웃 노드들의 정보에 따라 달라지며, aggregator function은 이러한 노드 임베딩 생성에 중요한 역할을 합니다.
GraphSAGE에서는 이웃 노드의 정보를 집계할 때, 각 노드의 이웃 노드들의 특징 벡터를 평균 또는 최대값으로 집계하는 방법을 사용한다. 즉, Aggregation function이 수행된 후, 각 노드의 특징 벡터는 이웃 노드들의 정보를 참조하여 새로운 값을 가지게 된다. 이 과정을 여러 번 반복하면, 각 노드의 특징 벡터는 그래프 내에서의 역할과 중요도에 따라 다양한 값으로 수렴하게 된다.
따라서 Aggregation function은 GraphSAGE에서 가장 중요한 구성 요소 중 하나다. 이 함수를 어떻게 구현하느냐에 따라 모델의 성능과 학습 속도가 크게 달라질 수 있다.
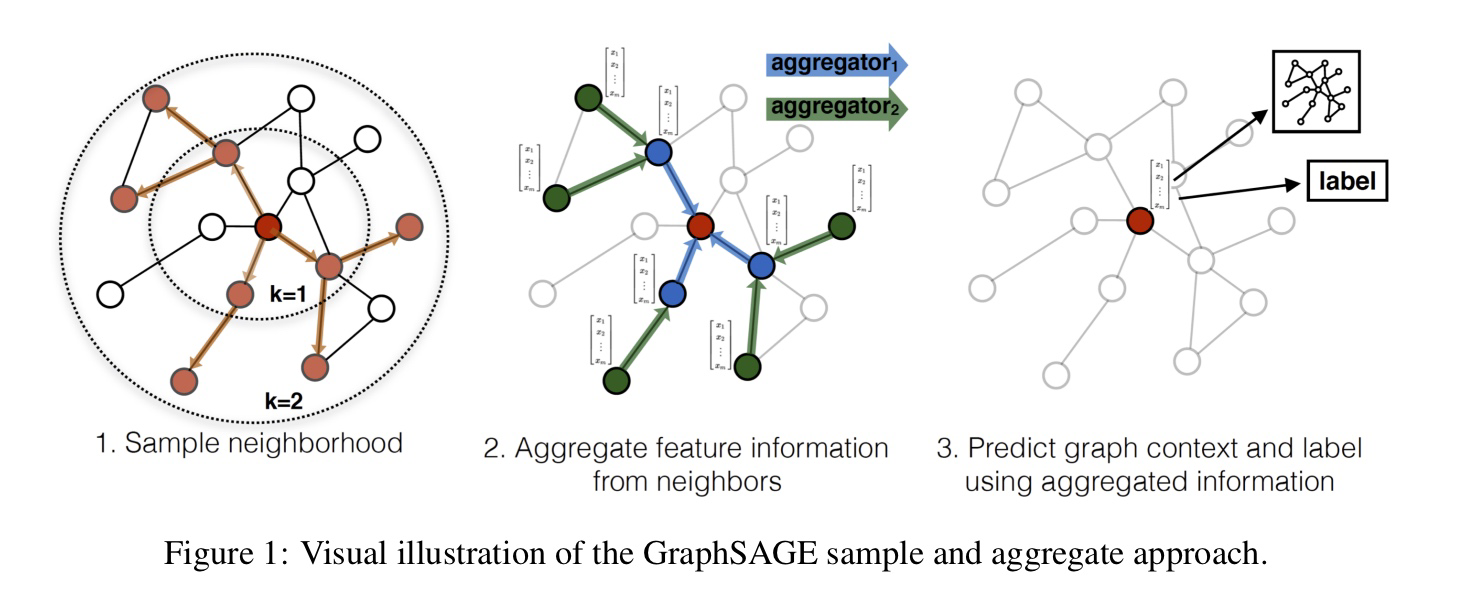
여기서 확인할 수 있는 직관은 각 iteration 혹은 search depth에서 Node는 그의 지역 이웃으로부터 정보들을 모으고, 이러한 과정이 반복되면서 Node는 Graph의 더 깊은 곳으로부터 정보를 증가시키면서 얻게 된다는 것이다.
알고리즘1은 Graph 구조와 Node Features가 Input으로 주어졌을 때의 Embedding 생성 과정에 대해 기술하고 있다. 아래에서는 Mini-batch 환경에서 어떻게 일반화할 수 있을지 설명할 것이다. 알고리즘1의 바깥 Loop의 각 단계를 살펴보면, hk 는 그 단계에서의 Node의 Representation을 의미한다.
Aggregation function은 인접한 노드들의 특징 벡터를 aggregate하여 target 노드의 새로운 특징 벡터를 생성합니다. 이 과정에서 각 노드의 특징 벡터는 그 노드의 이웃 노드들의 정보를 참조하여 업데이트됩니다.
GraphSAGE에서는 이웃 노드의 정보를 집계할 때, 각 노드의 이웃 노드들의 특징 벡터를 평균 또는 최대값으로 집계하는 방법을 사용합니다. 즉, Aggregation function이 수행된 후, 각 노드의 특징 벡터는 이웃 노드들의 정보를 참조하여 새로운 값을 가지게 됩니다. 이 과정을 여러 번 반복하면, 각 노드의 특징 벡터는 그래프 내에서의 역할과 중요도에 따라 다양한 값으로 수렴하게 됩니다.
- GraphSAGE 에서 aggregator function의 역할은?
GraphSAGE에서 aggregator function은 각 노드의 이웃 노드들의 정보를 모아서 노드의 Embedding을 생성하는 역할을 한다. 즉, 이웃 노드들의 특성을 집계해서 각 노드의 정보를 나타내는 벡터를 만드는 것이다. 각 aggregator function은 특정 깊이(hop)에서 노드의 이웃 노드들로부터 정보를 수집한다. 예를 들어, aggregator function이 2-hop aggregator인 경우, 노드의 이웃 노드와 이웃 노드의 이웃 노드들의 정보를 수집한다. 이렇게 수집한 정보를 기반으로 노드의 Embedding 벡터를 계산한다. 따라서, 각 노드의 Embedding은 Graph 내의 이웃 노드들의 정보에 따라 달라지며, aggregator function은 이러한 노드 Embedding 생성에 중요한 역할을 한다.
다시 정리하고 넘어가자면, 모델의 목적은 각 Node에 대한 고유의 Embedding 벡터를 학습하는 대신, Node의 지역 이웃으로부터 Feature 정보를 규합하는 Aggregator Function의 집합을 학습하는 것이다.
이렇게 추론된 새로운 노드에 대한 Embedding을 downstream task에 활용한다. 특정 노드의 Embedding을 계산할 때, 거리가 K 만큼 떨어져 있는 노드에서부터 순차적으로 feature aggregation을 적용하는 것이다.
- 왜 거리가 K 만큼 떨어져 있는 노드에서부터 aggregation을 적용하는 것일까? 가까운 노드에서부터 aggregation을 적용하지 않는 이유는?
우선, 거리가 가까운 이웃 노드들의 정보만을 이용하여 aggregation을 수행하게 되면 해당 노드의 embedding은 이웃 노드들의 정보만을 반영하게 된다. 이에 반해, 거리가 더 멀리 떨어진 이웃 노드들의 정보를 추가적으로 활용하면 해당 노드의 embedding은 보다 다양하고 전체적인 특성을 더 잘 반영할 수 있다. 또한, 거리가 멀어질수록 이웃 노드의 수는 기하급수적으로 늘어나게 된다. 이 때문에 모든 이웃 노드들의 정보를 동시에 고려하면 계산 복잡도가 증가하여 embedding을 계산하는 데 필요한 시간이 매우 오래 걸리게 된다. 이에 반해, 거리가 K 이상인 노드들의 정보를 순차적으로 적용하면 계산 복잡도를 낮추면서도 보다 다양한 이웃 노드들의 정보를 활용할 수 있다.
3-1. AutoEncoder
GraphSAGE에서 사용되는 AutoEncoder network는 인접 행렬의 재구성을 위해 사용됩니다. 이 때, 인접 행렬을 입력으로 받아 각 노드에 대한 임베딩 벡터를 출력하는 MLP를 인코더로 사용하고, 이를 다시 입력으로 받아 인접 행렬을 재구성하는 MLP를 디코더로 사용합니다. 따라서 GraphSAGE에서 사용되는 AutoEncoder network는 MLP의 일종이며, 인코더와 디코더가 각각 MLP로 구성되어 있습니다.
Aggregation Function과 AutoEncoder network는 GraphSAGE 모델의 두 부분으로, 각각이 서로 다른 역할을 합니다. Aggregation Function은 각 노드의 이웃 노드의 특징 벡터를 aggregate하여 target 노드의 특징 벡터를 생성하는 역할을 합니다. AutoEncoder network는 인접 행렬을 입력으로 받아서, 인접 행렬을 재구성하기 위한 잠재 변수(latent variable)을 학습합니다. 이렇게 학습된 잠재 변수는 각 노드에 대한 임베딩 벡터로 해석될 수 있습니다. 따라서, 인접 행렬은 AutoEncoder network의 입력이 되는 것입니다.
Aggregation Function은 AutoEncoder network의 입력으로 이용될 특징 벡터를 생성하는 과정 중 하나입니다. Aggregation Function은 이웃 노드들의 특징 벡터를 aggregate하여 target 노드의 새로운 특징 벡터를 생성하는 과정입니다. 이 과정에서 생성된 특징 벡터들은 AutoEncoder network의 입력으로 사용될 수 있습니다.
이러한 방식으로 Aggregation Function과 AutoEncoder network는 서로 협력하여 GraphSAGE 모델이 노드 분류, 노드 임베딩 등의 작업을 수행할 수 있게 됩니다.
- 인접 행렬이란?
인접 행렬(Adjacency Matrix)은 그래프에서 노드 간의 연결 상태를 나타내는 정사각형 행렬입니다. 보통은 대각선을 기준으로 대칭인 행렬을 사용합니다. 인접 행렬은 그래프의 구조 정보를 행렬로 나타내어 다양한 그래프 분석 기법에서 활용됩니다.
그래프의 인접 행렬은 다음과 같은 방식으로 데이터에서 도출할 수 있습니다. 먼저, 그래프의 노드 수를 n이라고 할 때, n x n 크기의 0 행렬을 생성합니다. 그리고 각 엣지 (i, j)에 대해, 인접 행렬의 (i, j)와 (j, i) 위치를 1로 바꿉니다. 만약 무방향 그래프가 아니라 방향 그래프라면, (i, j) 위치만 1로 바꾸고 (j, i) 위치는 바꾸지 않습니다. 이렇게 하면 인접 행렬이 생성됩니다.
GraphSAGE에서 인접 행렬은 노드들 간의 연결 정보를 바탕으로 구성되며, 각 노드는 해당 노드와 직접 연결된 노드들의 정보를 담고 있는 행 벡터로 표현됩니다. 인접 행렬의 크기는 노드의 개수에 비례하며, 각 행은 해당 노드와 직접 연결된 노드들을 나타냅니다.
4. Batch Sampling
GraphSAGE를 학습하는 과정에서는 batch단위로 연산이 이루어져야 하며, 위의 이론을 실제로 구현하기 위해서는 batch를 샘플링하는 방법과 node neighborhood에 대한 정의가 필요하다.
이러한 샘플링 과정이 없으면, 각 Batch의 메모리와 실행 시간은 예측하기 힘들며 계산량이 엄청나게 많아지기 때문이다.
Machine Learning with Graphs | 2021 | Lecture 17.2 - GraphSAGE Neighbor Sampling 강의 발췌
" 그래서, 강조하자면, GraphSAGE의 핵심 아이디어는 다음과 같다. 특정 노드의 Embedding을 계산하기 위해서는 해당 노드의 K-hop 이웃만 알면 된다는 통찰력에서 출발한다. 따라서 노드를 기반으로 한 미니배치 대신 K-hop 이웃에 기반한 미니배치를 생성하면 신뢰성 있는 방식으로 기울기를 계산할 수 있다. 다시 말해서, 노드를 미니배치에 넣는 대신, 계산 Graph 또는 K-hop 이웃을 미니배치에 넣는 것이다."
계산 Graph나 K-hop 이웃을 mini-batch에 어떻게 넣을 수 있다는 걸까?
미니배치에 계산 Graph나 K-hop 이웃을 넣기 위해서는 Graph를 인접 리스트나 인접 행렬로 나타내고, 미니배치를 생성할 때 이웃 노드들을 샘플링하여 Graph를 생성하는 과정이 필요하다. 이렇게 생성된 Graph는 pytorch-geometric의 NeighborSampler를 사용하여 미니 배치로 처리할 수 있으며 GPU와 함께 사용할 수도 있다. 이 때, 미니배치 내의 모든 Graph는 동일한 크기여야 하며, Graph 내의 모든 노드는 동일한 수의 이웃 노드를 가져야 한다. 이를 위해서는 적절한 샘플링 전략을 선택하여 이웃 노드를 선택해야 하며, 이웃 노드의 수가 일정하도록 맞추는 것이 중요한다.
그렇다면 Graph 내의 노드 중에서, 이웃을 단 1개만 가진 노드가 있을 경우에는?
GraphSAGE에서는 이웃을 가지지 않은 노드를 위해 self-loop를 추가한다. Self-loop는 노드 자신을 자신의 이웃으로 간주하고, 노드의 피처 벡터와 함께 이웃 노드 벡터를 집계하는 데 사용된다. 따라서 self-loop를 추가하면 모든 노드에 대해 일관된 방식으로 이웃 정보를 수집할 수 있다.
5. Aggregator Architectures
aggregator function은 이웃 노드들로부터의 정보를 aggregate하는 역할을 한다. N차원의 격자 구조 데이터를 이용한 머신러닝 예(텍스트, 이미지 등)들과 달리, Node의 이웃들은 자연적인 어떤 순서를 갖고 있지 않다. 하지만 Graph 데이터의 특성 상, 노드의 neighborhood들 간에는 어떤 순서가 없다. 따라서, aggregator function은 symmetric하고 높은 수용력(high representational capacity)을 지님을 동시에 학습 가능해야 한다. 기본적으로 Aggregator Function은 반드시 순서가 정해져있지 않은 벡터의 집합에 대해 연산을 수행해야 하기 때문이다.
Aggregator Funcion의 대칭성은 우리의 신경망 모델이 임의의 순서를 갖고 있는 Node 이웃 feature 집합에도 학습/적용될 수 있게 한다. 본 논문은 이에 대해 3가지 후보를 검증했다.
- Mean Aggregator : 주변 노드의 Embedding과 자기 자신(ego node)의 Embedding을 단순 평균한 후, 선형 변화와 relu를 적용해 줌으로써, Embedding을 업데이트. 단지 벡터의 원소 평균을 취한 함수이다.
- LSTM Aggregator : LSTM aggregator는 높은 수용력을 가진다는 장점을 갖고 있다. LSTM의 경우 표현력에 있어서 장점을 지니지만 하지만 LSTM 자체는 symmetric한 함수가 아니라는 문제가 있다. permutation invariant 하지 않다. 따라서 본 연구에서는, 인풋 노드들의 순서를 랜덤하게 조합하는 방식을 취한다. 따라서 본 논문에서는 LSTM을 Node의 이웃의 Random Permutation에 적용함으로써 순서가 없는 벡터 집합에 대해서도 LSTM이 잘 동작하도록 했다.
- Pooling Aggregator : 각 노드의 Embedding에 대해 선형 변환(linear transformation)을 수행한 뒤, element-wise max pooling을 통해 이웃 노드들의 정보를 aggregate하는 방식. 각 이웃의 벡터는 독립적으로 fully-connected된 신경망에 투입된다. 이후 이웃 집합에 Elementwise max-pooling 연산이 적용되어 정보를 통합한다. 이론 상으로 max-pooling 이전에 여러 겹의 layer를 쌓을 수도 있지만, 본 논문에서는 간단히 1개의 layer 만을 사용하였는데, 이 방법은 효율성 측면에서 더 나은 모습을 보여준다. 계산된 각 피쳐에 대해 max-pooling 연산을 적용함으로써 모델은 이웃 집합의 다른 측면을 효과적으로 잡아내게 된다. 물론 이 때 어떠한 대칭 벡터 함수든지 max 연산자 대신 사용할 수 있다. 본 논문에서는 max-pooling과 mean-pooling 사이에 있어 큰 차이를 발견하지 못하였고 이후 논문에서는 max-pooling을 적용하는 것으로 과정을 통일했다.
- 어떤 방식이 가장 좋을까?
Max-Pooling은 주변 노드들 중에서 가장 중요한 feature를 추출하기 때문에 노이즈가 있는 데이터나 sparse한 데이터에서 좋은 성능을 발휘할 수 있다. 하지만 Mean-Aggregating을 사용하면 더 간단하고 빠른 학습을 할 수 있으며, 높은 성능을 발휘하는 경우도 있다. 따라서 GraphSAGE에서는 이 두 방법 중에서 적절한 방법을 선택하는 것이 중요하다고 볼 수 있다.
6. Learning Graphsage
본 논문에서 제안하는 것을 다시 정리해보자면, 각 노드들의 feature를 aggregate함으로써 "각 노드의 Embedding을 추론할 수 있는 aggregator function의 파라미터를 학습하는 것이다.
이제는 train에 대해 이야기해 보도록 한다. 본 모델의 optimization objective는 기존의 node2vec과 같은 shallow embedding network와 크게 다르지 않다. K iteration 후의 node representation인 z u,u∈V에 대해 손실함수가 계산되며, aggregator function의 파라미터인 Wk ,k∈{1,2,..,K}가 gradient descent를 통해 학습된다.
zv와 zu 는 random walk를 기반으로 이웃으로 설정된 노드 쌍이고, zvn은 z u에 대한 negative node(이웃이 아닌 노드)이다. 즉, 이웃 노드끼리는 유사도가 높은 Embedding을 갖도록, 이웃이 아닌 노드끼리는 유사도가 낮은 Embedding을 갖도록 학습이 이루어지게 된다.
- Random Walk와 K-hop sampling은 서로 다른 샘플링 방법입니다.
Random Walk는 임의의 노드에서 시작해서, 그 노드의 이웃 중에서 무작위로 하나를 선택한 후 이동합니다. 이동한 노드에서도 마찬가지로 이웃 중에서 무작위로 하나를 선택하고 이동합니다. 이런식으로 랜덤하게 노드를 이동하는 것을 반복하여 원하는 길이의 시퀀스를 생성합니다. 이렇게 생성된 시퀀스를 이용하여 그래프에서 노드 샘플링을 할 수 있습니다.
반면에 K-hop sampling은 임의의 노드에서 시작해서, 이웃 노드를 K번 탐색하여 이들을 샘플링합니다. 이러한 방식으로 샘플링된 노드들을 이용하여 인접 행렬을 생성합니다.
따라서 둘은 샘플링 방법이 다르며, Random Walk는 시퀀스를 생성하는 것이 목적이고, K-hop sampling은 인접 행렬을 생성하는 것이 목적입니다.
6-1 . Paremeters of GraphSAGE
완전한 비지도 학습 상황에서 유용하고 예측 능력이 있는 Representation을 학습하기 위해서는 Graph 기반의 Loss 함수를 Output Represnetation에 적용하고, Weight Matrices 및 Stochastic Gradient Descent를 통해 Aggregator Funciton의 파라미터를 튜닝해야 한다.
Graph 기반의 Loss 함수는 인접한 Node들이 유사한 Representation을 갖도록 하게 하고 서로 멀리 떨어져 있는 Node들은 다른 Representation을 갖게 만든다.
이 때 v 는 고정된 길이의 Random Walk 에서 u 근처에서 동시에 발생한 Node를 의미한다. Pn 은 Negative Sampling Distribution을 Q 는 Negative Sample의 개수를 의미한다.
- Random Walk 란?
Random Walk란, Graph에서 시작 노드에서 시작하여 무작위로 이웃 노드를 선택하여 이동하면서 일정 길이의 경로를 따라가는 것을 말한다. 즉, 무작위로 이웃 노드를 선택하고 이동하는 과정을 반복하여 Graph 상에서 랜덤한 경로를 탐색하는 것이다.
이를 이용해 랜덤하게 샘플링하여 Graph 내의 다양한 노드들을 탐색하고, 이를 통해 Graph 전체를 대표하는 Embedding을 학습하는 방법이 있다. 이때, Random Walk의 길이는 학습하고자 하는 Graph의 특성에 따라 다양하게 설정될 수 있다.
중요한 점 : Graph 기반의 Loss 함수인 zu는 Graph 내 노드들의 Embedding을 학습하기 위한 함수이다. 하지만, 이 함수에서는 이전의 Embedding 방법과 달리 각 노드의 고유한 Embedding을 직접적으로 학습하지 않다. 대신, Graph에서 추출한 정보를 바탕으로 각 노드의 Embedding을 도출한다. 즉, 노드의 이웃 정보 등을 사용해 Graph 전체에 대한 Embedding을 학습하고, 그 결과를 각 노드에 적용함으로써 각 노드의 Embedding을 구하는 방식이다. 이 방식은 비지도 학습에서 유용하며, 예측 능력이 있는 Embedding을 학습할 수 있도록 도와준다.
7. Experiments
본 논문에서 GraphSAGE의 성능은 총 3가지의 벤치마크 task에서 평가되었다.
(1) Web of Science citation 데이터셋을 활용하여 학술 논문을 여러 다른 분류하는 것
(2) Reddit에 있는 게시물들이 속한 커뮤니티를 구분하는 것
(3) 다양한 생물학적 Protein-protein interaction Graph 속에서 protein 함수를 구별하는 것
LSTM, Pooling 기반의 Aggregator가 가장 좋은 성능을 보였다. K=2로 설정하는 것이 효율성 측면에서 좋은 모습을 보여주었고, 이웃 개체들을 sub-sampling하는 것은 비록 분산을 크게 만들지만 시간을 크게 단축되기 때문에 꼭 필요한 단계라고 할 수 있겠다.
8. Code
import os
import sys
import torch
import torch.nn.functional as F
from tqdm import tqdm
from torch_geometric.datasets import Reddit
from torch_geometric.data import NeighborSampler
from torch_geometric.nn import SAGEConv
sys.path.append('./')
from utils import *
logger = make_logger(name='graphsage_logger')
# Load Reddit Dataset
path = os.path.join(os.getcwd(), '..', 'data', 'Reddit')
dataset = Reddit(path)
data = dataset[0]
# Data 확인
# Nodes: 232965, Node Features: 602
logger.info(f"Node Feature Matrix Info: # Nodes: {data.x.shape[0]}, # Node Features: {data.x.shape[1]}")
# Edge Index
# Graph Connectivity- COO (2, num_edges)형태의 그래프 연결 = (2, 114,615,892=1.14억)
logger.info(f"Edge Index Shape: {data.edge_index.shape}")
logger.info(f"Edge Weight: {data.edge_attr}")
# train_mask는 훈련할 nodes을 나타낸다. (153431 nodes)
print(data.train_mask.sum().item())
### output
graphsage_logger - Node Feature Matrix Info: # Nodes: 232965, # Node Features: 602
graphsage_logger - Edge Index Shape: torch.Size([2, 114615892])
graphsage_logger - Edge Weight: None해당 그래프에 총 232,965개의 노드가 존재한다는 건, 그래프를 구성하는 user와 item 개수가 총 232,965개라는 것.
"노드당 602개의 feature가 존재한다"는 게 정확히 무슨 의미?
각 노드가 602차원의 벡터로 표현된다.
각 user와 item이 602개의 특징(예를 들어, 성별, 나이, 관심사 등)을 가지고 있다. (이러한 특징을 벡터 형태로 표현한 것)
"첫번째 차원은 각 엣지의 시작점, 두번째 차원은 각 엣지의 종료점을 의미"한다는 게 이해가 안 돼. 엣지의 시작점과 종료점이라는 게 정확히 뭐야?
- 그래프에서 엣지(간선)는 노드(정점) 간의 관계를 나타냅니다. 예를 들어, A와 B 두 노드가 연결된 엣지를 생각해보면, A는 이 엣지의 시작점, B는 종료점입니다. 엣지를 표현하는 인덱스는 (시작점 노드의 인덱스, 종료점 노드의 인덱스) 형태이며, 이 때 첫번째 차원은 시작점 노드의 인덱스를, 두번째 차원은 종료점 노드의 인덱스를 나타냅니다. 따라서 (0, 1)은 0번 노드에서 1번 노드로 이어지는 엣지를 나타냅니다.
그래프의 엣지 가중치 정보가 없을 수도 있어?
- 네, 그래프에 엣지 가중치 정보가 없는 경우가 있습니다. 일반적으로 그래프 데이터는 네트워크 구조를 표현하는데 초점을 맞추기 때문에, 엣지 가중치 정보가 없는 경우가 많습니다. 엣지 가중치 정보가 없는 경우에는 모든 엣지에 대해 가중치가 1로 설정되어 있는 것으로 간주됩니다.
그러면 엣지 가중치 정보는 모델 학습이 진행되면서 갱신되겠네? - 네, 그렇습니다. 일반적으로 그래프 신경망 모델에서 엣지 가중치는 초기에 무작위로 초기화되며, 학습 도중에 최적화되어 업데이트됩니다. 모델이 학습을 진행하면서 예측과 정답 간의 오차를 최소화하는 방향으로 엣지 가중치가 업데이트되는 과정을 통해 모델이 데이터에 더 잘 맞도록 학습합니다.
# Define Sampler
train_loader = NeighborSampler(
data.edge_index, node_idx=data.train_mask,
sizes=[25, 10], batch_size=1024, shuffle=True, num_workers=12)
subgraph_loader = NeighborSampler(
data.edge_index, node_idx=None,
sizes=[-1], batch_size=1024, shuffle=False, num_workers=12)NeighborSampler Size
sizes=[25, 10]는 Neighbor Sampling에서 사용할 k-hop 크기를 나타낸다.
sizes 리스트의 첫 번째 값인 25는 1-hop neighbor와 2-hop neighbor까지 사용하여 샘플링할 개수를 의미한다. 이는 중심 노드와 인접한 노드, 그리고 이들의 이웃 노드까지 모두를 포함하여 최대 25개까지 샘플링한다는 것을 뜻한다. 즉, 이 값은 한 번에 샘플링할 이웃 노드의 최대 수를 결정하는 것이다.
두 번째 sizes 값인 10은 샘플링할 이웃 노드의 개수를 의미한다. 이 값은 첫 번째 값과는 다르게 1-hop neighbor에 대해서만 샘플링을 하며, 2-hop neighbor는 사용하지 않는다. 따라서 이 값은 첫 번째 값보다 작다.
예를 들어, 1-hop neighbor가 A, B, C, D, E, F인 노드 u에 대해 첫 번째 값 25와 두 번째 값 10을 가진 sizes를 사용하면 다음과 같은 샘플링이 이루어진다.
1) 1-hop neighbor에서 25개 노드를 샘플링한다. 예를 들어, A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y가 선택된다.
1-2) 2-hop neighbor에서 25개 노드를 샘플링한다. 예를 들어, 2-hop neighbor가 a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y일 때, A와 이웃인 a, b, c, d, e와 B와 이웃인 f, g, h, i, j를 선택한다.
2) 1-hop neighbor에서 10개 노드를 샘플링한다. 예를 들어, A, B, C, D, E, F, G, H, I, J가 선택된다.
즉, 첫 번째 값은 1-hop neighbor와 2-hop neighbor까지 모두 사용하여 샘플링하며, 두 번째 값은 1-hop neighbor에 대해서만 샘플링한다. 이는 모델의 복잡도를 조절할 수 있는 하이퍼파라미터이다.
이렇게 여러 개의 k-hop 크기를 사용하여 샘플링하는 것은 더 넓은 범위의 이웃 노드 정보를 포함할 수 있도록 하여 모델 성능을 높일 수 있다.
sizes는 하나의 리스트로 구성되어 있으며, 리스트 내의 값이 클수록 더 많은 이웃 노드 정보를 사용하여 샘플링한다.
num_workers
num_workers는 NeighborSampler가 데이터를 로딩할 때 사용할 worker(thread)의 수를 의미한다. 즉, 병렬적인 데이터 로딩을 위한 파라미터이다. 이 값을 높일수록 데이터 로딩 속도가 빨라지지만, 시스템 리소스를 많이 사용하게 되어 메모리나 CPU 사용량 등을 고려하여 적절한 값을 선택해야 한다. 기본값은 1이며, 사용 가능한 하드웨어 리소스에 따라 값을 조정할 수 있다.
subgraph_loader와 train_loader
train_loader는 훈련 데이터셋을 위한 Neighbor Sampling을 수행한다. 이 때 node_idx 인자에는 훈련 데이터셋에서 사용될 노드 인덱스를 전달한다.
반면에 subgraph_loader는 일반적으로 테스트 데이터셋에서 사용된다. node_idx 인자에는 None 값을 전달한다. sizes 인자는 -1로 설정하여 원래 그래프 전체를 사용하지 않고, 부분 그래프(subgraph)를 샘플링한다. 이렇게 샘플링된 부분 그래프는 전체 그래프의 근사값(approximation)으로 사용된다.
batch_size, n_id, adjs = next(iter(train_loader))
logger.info(f"Current Batch Size: {batch_size}")
logger.info(f"현재 Subgraph에서 사용된 모든 node id의 개수: {n_id.shape[0]}")
logger.info(f"Layer의 수: {len(adjs)}")
A = adjs[1].size[0] - batch_size
B = adjs[0].size[0] - A - batch_size
logger.info(f"진행 방향: {B}개의 2-hop neighbors ->"
f"{A}개의 1-hop neighbors -> {batch_size}개의 Head Nodes")
### output
graphsage_logger - Current Batch Size: 1024
graphsage_logger - 현재 Subgraph에서 사용된 모든 node id의 개수: 106532
graphsage_logger - Layer의 수: 2
진행 방향: 84747개의 2-hop neighbors ->20761개의 1-hop neighbors -> 1024개의 Head NodesGraphSAGE 모델이 한 번의 forward propagation을 수행할 때의 상세 정보
현재 처리되고 있는 배치 크기가 1024
현재 subgraph에서 사용된 모든 노드의 개수가 106532개 (subgraph는 해당 배치의 노드와 그 이웃 노드들로 구성된 작은 그래프)
GraphSAGE 모델이 2개의 GraphSAGE 레이어로 구성되어 있음
현재 배치의 노드들을 중심으로 하는 subgraph에서, 먼저 2-hop 이웃 노드 84747개를 집계하고, 그 다음 1-hop 이웃 노드 20761개를 집계한 뒤, 마지막으로 이 중심 노드 1024개를 Head 노드로 사용하여 모델을 실행하고 있음(이러한 방식으로 이웃 노드를 집계하여 Head 노드의 임베딩 벡터를 생성하고, 모델 학습을 수행)
-
batch_size : 현재 batch size를 의미함 (integer)
next(iter(train_loader))를 호출하면, batch_size에 해당하는 개수의 샘플들을 반환한다. 이때 반환된 데이터는 이전에 NeighborSampler에서 지정한 sizes 파라미터에 따라 다양한 크기의 서브그래프(subgraph)를 형성한다. 따라서 n_id는 현재 배치에 있는 모든 노드 ID를 담고 있으며, adjs는 현재 배치에 대해 형성된 서브그래프의 리스트이다. 이 서브그래프들은 이후 모델 학습에서 사용된다. -
n_id : 이번 Subgraph에서 사용된 모든 node id.
batch_size개의 Row를 예측하기 위해서는 1차 이웃 node A개가 필요하고, 1차 이웃 node A개를 위해서는 2차 이웃 node B개가 필요.
n_id.shape = batch_size + A + B -
adjs : 아래와 같이 Layer의 수가 2개이면 adjs는 길이 2의 List가 된다.(subgraph의 리스트)
head node가 있고 1-hop neighbors와 2-hop neighbors가 있다고 할 때, adjs[0]은 1번째 레이어(1-hop 이웃)와 관련된 정보를 나타내며, head node와 1-hop 이웃들의 관계를 설명한다.
adjs[1]은 2번째 레이어(2-hop 이웃)와 관련된 정보를 나타내며, 1-hop 이웃들과 2-hop 이웃들 간의 관계를 설명한다. -
각 리스트에는 (edge_index, e_id, size) 튜플이 들어있다.
edge_index: source -> target nodes를 기록한 bipartite edges
e_id: 위 edge_index에 들어있는 index가 Full Graph에서 갖는 node id
size: 위 edge_index에 들어있는 node의 수를 튜플로 나타낸 것으로 head -> 1-hop 관계를 예시로 들면, head node의 수가 a개, 1-hop node의 수가 b개라고 했을 때 size = (a+b, a). 또한 target node의 경우 source nodes의 리스트의 시작 부분에 포함되어 있어 skip-connections나 self-loops를 쉽게 사용할 수 있게 되어 있다.
4-1. bipartite edges
Bipartite edge는 두 개의 독립된 노드 집합 간의 엣지를 의미한다. 예를 들어, 영화 추천 시스템에서 사용되는 경우, 한 집합은 사용자 노드이고 다른 집합은 영화 노드이다. 이 때, 사용자와 영화 간의 평점을 나타내는 엣지는 bipartite edge가 된다. 일반적으로, bipartite edge는 각 집합 내에서는 연결되어 있지 않으며 다른 집합 내의 노드와만 연결되어 있다.
4-2. edge
edge란 그래프에서 노드들 간의 연결을 의미하는 선이다. edge는 노드들 간의 상호작용을 모델링하는 데 사용된다. 예를 들어, 소셜 네트워크에서 두 사람 간의 친구 관계, 도시 간의 도로, 단어 간의 유사도 등을 edge로 모델링할 수 있다. 따라서 edge는 그래프 신경망에서 정보 전달과 모델의 예측을 수행하는 중요한 역할을 한다.
- edge_attr, edge_index?
edge_index는 각 엣지의 시작 노드와 끝 노드의 인덱스를 나타내는 텐서다. 예를 들어, (2, 4)가 edge_index에 있다면, 2번 노드와 4번 노드 사이에 엣지가 존재한다는 것을 의미한다. edge_attr은 엣지의 특성 값을 나타내는 텐서이며, 예를 들어 엣지의 가중치나 거리 등을 나타낼 수 있다. 따라서 edge_index와 edge_attr은 서로 다른 정보를 담고 있는 텐서다.
# Define Model
class SAGE(torch.nn.Module):
def __init__(self, in_channels, hidden_channels, out_channels):
super(SAGE, self).__init__()
self.num_layers = 2
self.convs = torch.nn.ModuleList()
self.convs.append(SAGEConv(in_channels, hidden_channels))
self.convs.append(SAGEConv(hidden_channels, out_channels))
def forward(self, x, adjs):
for i, (edge_index, _, size) in enumerate(adjs):
x_target = x[:size[1]] # Target nodes 는 항상 먼저 placed된다.
x = self.convs[i]((x, x_target), edge_index)
# 마지막 Layer는 Dropout을 적용하지 않는다.
if i != self.num_layers - 1:
x = F.relu(x)
x = F.dropout(x, p=0.5, training=self.training)
return x.log_softmax(dim=-1)
def inference(self, x_all):
pbar = tqdm(total=x_all.size(0) * self.num_layers)
pbar.set_description('Evaluating')
# # 모든(All) 사용 가능한 edges를 사용하여 노드 표현을 계층별로 계산한다.
# 이는 각 batch의 final representations을 즉시 계산하는 것과 대조적으로
# 더 빠른 계산으로 이어진다.
for i in range(self.num_layers):
xs = []
for batch_size, n_id, adj in subgraph_loader:
edge_index, _, size = adj.to(device)
x = x_all[n_id].to(device)
x_target = x[:size[1]]
x = self.convs[i]((x, x_target), edge_index)
if i != self.num_layers - 1:
x = F.relu(x)
xs.append(x.cpu())
pbar.update(batch_size)
x_all = torch.cat(xs, dim=0)
pbar.close()
return x_allSAGE 클래스는 PyTorch의 nn.Module 클래스를 상속받고 있다. init 메서드에서는 SAGE 모델의 레이어들을 정의한다.
in_channels : 입력 feature의 차원 수.
hidden_channels : hidden feature의 차원 수
out_channels : 출력 feature의 차원 수
이 예제에서는 두 개의 레이어를 사용하고 있으며, 두 번째 레이어의 출력 feature의 차원 수는 out_channels로 정의된다.
self.convs는 SAGEConv 레이어를 저장하는 PyTorch의 nn.ModuleList 객체다. nn.ModuleList는 nn.Module 객체를 저장하는 파이썬 리스트와 비슷한 객체다.
forward 메서드는 모델의 forward propagation을 수행한다. 입력으로 x와 adjs를 받고, x는 그래프의 노드 feature 행렬이며, adjs는 그래프의 인접 리스트다.
adjs는 다음과 같은 형태의 튜플의 리스트이다:
edge_index: 그래프의 에지 인덱스를 나타내는 LongTensor
e_id: 사용되지 않음
size: 각 노드 수를 담은 LongTensor
각 레이어에서는 SAGEConv 레이어를 사용하고 있다. 레이어의 입력으로는 (x, x_target)이 사용된다. x는 모든 노드의 feature이고, x_target은 현재 샘플링된 노드의 feature이다. 이러한 방식으로 모델은 그래프의 전체 노드 feature 행렬을 가져오는 대신, 현재 샘플링된 노드들의 feature만을 사용하여 학습한다.
각 레이어에서 마지막에 relu 함수를 거친 뒤 dropout이 적용된다. 마지막 레이어에서는 log_softmax 함수를 사용하여 출력을 생성한다.
추론 함수는 다음과 같다 :
주어진 데이터 x_all에 대해서, num_layers 개수만큼 SAGEConv 레이어를 통해 embedding vector를 계산한다. 이를 위해, subgraph_loader에서 가져온 각 배치(batch)에 대해서 subgraph를 생성하고, 해당 subgraph에서 x_all에서 선택한 노드에 대한 인접 노드들의 embedding vector를 사용하여 새로운 embedding vector를 계산한다.
반복문이 돌면서 계산한 embedding vector는 x_all에 이어 붙여, 다음 SAGEConv 레이어에 대한 입력으로 사용된다. 이렇게 여러 레이어를 거쳐 최종 embedding vector를 계산한다.
이 과정에서 tqdm 모듈을 사용하여 계산 진행 상황을 표시하고, 계산이 완료되면 최종 embedding vector를 반환한다.
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = SAGE(dataset.num_features, 256, dataset.num_classes)
model = model.to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
x = data.x.to(device)
y = data.y.squeeze().to(device)PyTorch를 사용하여 GraphSAGE 모델을 정의하고, 데이터셋을 로드하고, 모델을 학습하기 위한 optimizer를 설정
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu'): GPU가 사용 가능한 경우 GPU를, 그렇지 않은 경우 CPU를 사용하여 모델 학습을 진행.
model = SAGE(dataset.num_features, 256, dataset.num_classes): GraphSAGE 모델을 정의. 입력 특성의 크기는 dataset.num_features이고, 은닉층의 크기는 256이며, 출력의 크기는 클래스 수(dataset.num_classes)와 같다.
model = model.to(device): 모델을 지정된 device(GPU 또는 CPU)로 이동한다.
optimizer = torch.optim.Adam(model.parameters(), lr=0.01): 모델의 파라미터를 최적화하기 위해 Adam optimizer를 사용하며, 학습률은 0.01로 설정된다.
x = data.x.to(device): 입력 데이터의 특성을 GPU 또는 CPU로 이동한다.
y = data.y.squeeze().to(device): 입력 데이터의 레이블을 GPU 또는 CPU로 이동한다. 레이블은 1차원 벡터로 변환되며, squeeze() 메서드를 사용하여 크기가 1인 차원을 제거한다.
# 학습
def train(epoch):
model.train()
pbar = tqdm(total=int(data.train_mask.sum()))
pbar.set_description(f'Epoch {epoch:02d}')
total_loss = total_correct = 0
for batch_size, n_id, adjs in train_loader:
# `adjs` 는 `(edge_index, e_id, size)` tuples의 list를 가지고 있다.
adjs = [adj.to(device) for adj in adjs]
optimizer.zero_grad()
out = model(x[n_id], adjs)
loss = F.nll_loss(out, y[n_id[:batch_size]])
loss.backward()
optimizer.step()
total_loss += float(loss)
total_correct += int(out.argmax(dim=-1).eq(y[n_id[:batch_size]]).sum())
pbar.update(batch_size)
pbar.close()
loss = total_loss / len(train_loader)
approx_acc = total_correct / int(data.train_mask.sum())
return loss, approx_acc
# 모델 평가
@torch.no_grad()
def test():
model.eval()
out = model.inference(x)
y_true = y.cpu().unsqueeze(-1)
y_pred = out.argmax(dim=-1, keepdim=True)
results = []
for mask in [data.train_mask, data.val_mask, data.test_mask]:
results += [int(y_pred[mask].eq(y_true[mask]).sum()) / int(mask.sum())]
return resultsmodel.train()은 모델을 학습 모드로 설정한다. pbar는 tqdm 라이브러리를 사용하여 현재 학습 진행 상황을 시각화하며, total_loss는 현재까지 누적된 loss 값, total_correct는 현재까지 누적된 정확도 값이다.
train_loader에서는 NeighborSampler를 사용하여 주어진 노드의 이웃 노드들을 샘플링하고, 이를 이용하여 mini-batch를 구성한다. 구성된 mini-batch는 batch_size, n_id, adjs로 구성되어 있다.
adjs는 train_loader에서 샘플링된 mini-batch 내의 모든 노드에 대한 이웃 정보를 담고 있는 리스트이다. 이 리스트의 각 요소는 (edge_index, e_id, size)의 튜플이다. edge_index는 샘플링된 mini-batch 내의 노드들 간의 edge 정보를 담고 있으며, size는 각 노드의 이웃 노드들의 개수를 담고 있다.
optimizer.zero_grad()를 호출하여 optimizer의 gradient를 0으로 초기화하고, 모델의 입력으로 mini-batch 내의 노드의 feature와 샘플링된 adjs 정보를 입력으로 넣어 출력을 계산한다. 출력값 out은 softmax 함수를 거쳐 클래스별 확률 값을 가지는 tensor이다. 이 tensor를 이용하여 NLLLoss를 계산하고 backward하여 gradient를 계산한다. 이후 optimizer를 이용하여 모델의 weight를 업데이트한다.
마지막으로 total_loss와 total_correct에 각각 loss와 정확도 값을 더한다. total_loss는 mini-batch의 개수로 나누어 loss의 평균값을 구하고, total_correct는 학습 데이터셋 내에서 모델이 맞힌 레이블의 개수를 학습 데이터셋의 크기로 나누어 정확도를 구한다.
@torch.no_grad() 데코레이터는 해당 함수 내에서의 모든 계산이 경사도를 계산하지 않기 위해 with 구문 대신 사용되며, 이 함수 내에서의 모든 텐서 연산이 추적되지 않는다.
이후에는 모델을 평가하기 위해 필요한 준비 작업들이 이루어진다. model.eval()은 모델을 평가 모드로 설정하며, model.inference(x)는 모든 노드를 대상으로 한번에 계산을 수행하는 inference 함수를 호출한다. 이 함수는 앞서 살펴본 대로 subgraph sampling을 수행하여 모든 노드를 대상으로 한 번에 계산한다.
계산된 out 텐서에서는 argmax를 통해 가장 큰 값을 가지는 클래스를 예측값으로 설정한다. 그리고 이 예측값과 정답값 y_true를 비교하여 모델의 성능을 측정한다.
마지막으로, 성능 측정을 위해 data.train_mask, data.val_mask, data.test_mask를 순회하며 예측 결과를 저장하고, 결과를 반환한다.
for epoch in range(1, 3):
loss, acc = train(epoch)
print(f'Epoch {epoch:02d}, Loss: {loss:.4f}, Approx. Train: {acc:.4f}')
train_acc, val_acc, test_acc = test()
print(f'Train: {train_acc:.4f}, Val: {val_acc:.4f}, Test: {test_acc:.4f}')
### output
Epoch 01, Loss: 0.5166, Approx. Train: 0.9219
Evaluating: 100%|██████████| 465930/465930 [07:19<00:00, 1061.07it/s]
Train: 0.9550, Val: 0.9500, Test: 0.9484
Epoch 02: 100%|██████████| 153431/153431 [03:12<00:00, 798.44it/s]
Epoch 02, Loss: 0.5452, Approx. Train: 0.9249
Evaluating: 100%|██████████| 465930/465930 [07:16<00:00, 1068.18it/s]Train: 0.9583, Val: 0.9506, Test: 0.9503train 함수를 이용해 모델을 학습하고, 학습 결과를 출력
range(1,3)은 1부터 2까지 (3은 포함하지 않음)의 숫자를 갖는 리스트를 만든다. 이는 총 2번의 학습(epoch)을 수행한다는 뜻.
loss, acc = train(epoch)는 train 함수에서 반환된 손실값과 정확도를 loss와 acc에 저장한다.
print(f'Epoch {epoch:02d}, Loss: {loss:.4f}, Approx. Train: {acc:.4f}')은 현재 학습 epoch 번호, 손실값, 정확도를 출력하는 코드다.
test 함수를 이용하여 각 에폭에서의 학습과 평가 결과를 함께 출력한다.
각 에폭에서 평균 손실이 상승하면서, train 데이터셋의 정확도(approx. train)는 약간 상승. 또한, validation 데이터셋과 test 데이터셋에서의 정확도는 전반적으로 비슷한 수준을 보이고 있다.
사실, GraphSAGE 모델은 임베딩 기술의 하나로 볼 수 있다. GraphSAGE 모델은 그래프의 구조 정보를 활용하여 노드의 임베딩을 생성하는데, 이는 Node2Vec 알고리즘의 임베딩 생성 방식과 유사하다. 따라서, 노드 임베딩을 생성하는 두 방법은 상호 보완적이며, 동일한 문제에 대해 각각의 장단점이 있다. 더 나아가, Node2Vec 알고리즘의 임베딩과 GraphSAGE 모델의 임베딩을 결합하여 더욱 향상된 임베딩을 생성하는 연구도 진행되고 있다.
