LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation

PAPER
본 논문은 기존의 협업 필터링 방식에 그래프를 접목한 논문이며 LightGCN은 기존의 그래프 기반 추천시스템에서 불필요한 부분을 없애고 추천에 필요한 부분만 사용해서 말 그대로 light하면서도 좋은 성능을 보인 모델입니다❕

ABSTRACT

기존 GCN(Graph Convolution Network)은 협업 필터링에서 SOTA를 달성하였으나 추천시스템에서 효과적인 이유를 설명하기 어려웠음.
GCN은 원래 그래프 분류 태스크를 위해 설계되었던 모델이고 많은 neural entwork operation을 갖추고 있음.

💡 GCN의 가장 흔한 설계인 feature transformation과 nonlinear activation이 협업 필터링 성능에 별로 기여하지 않음을 발견❕
➕ 훈련의 어려움🔺, 추천 성능🔻
➡ GCN 모델을 단순화해서 추천에 적합하도록 만들자 (LightGCN)

user-item embeddings를 user-item interaction graph에서 선형적으로 전파하고(linearly propagating), 모든 레이어에서 학습된 임베딩의 가중합을 최종 임베딩으로 사용

INTRODUCTION

CF(Collaborative Filtering, 협업 필터링)의 가장 일반적인 패러다임은 user와 item을 나타내는 latent feature(즉, embedding)을 학습하고, embedding vector를 기반으로 예측을 수행하는 것.
❗ NGCF는 GCN의 구조를 차용했고 CF에서 SOTA를 달성했지만, 본 논문의 저자들은 CF구조에 적절하지 않다고 주장

GCN 모델은 노드 분류를 위해 제안되었기 때문에 각 노드(user or item)가 단순히 식별자인 one-hot ID로만 표현됨.
이러한 간단한 입력에 대해 여러 층의 비선형 특성 변환을 수행(복잡한 모듈 사용)하는 것은 모델 훈련의 어려움만 증가하고 긍정적인 영향을 없을 것이라고 생각
➡ NGCF에 대한 ablation studies

• feature transformation과 nonlinear activation이 NGCF의 효과에 기여❌
• 오히려 연산을 제거함으로써 모델의 성능🔺

CF을 위해 GCN의 neighborhood aggregation을 포함한 LightGCN 제안

❶ 각 user(item)에 ID embedding을 연결
❷ user-item interaction graph에 embedding을 전파
❸ 다양한 propagation layer에서 학습된 embedding을 가중합으로 결합하여 예측을 위한 최종 임베딩을 얻음

✅ 논문에서 하고자 하는 일들

• GCN의 feature transformation과 nonlinear activation이 CF에 긍정적인 영향을 미치지 않음을 보이기
• LightGCN 제안 - 추천을 위해 GCN의 가장 필수적인 구성 요소만 포함하여 모델 단순화
• 동일한 환경에서 NGCF와 LightGCN을 비교하여 개선됨을 보이기
  
  

PRELIMINARIES

NGCF Brief

NGCF의 embedding rule

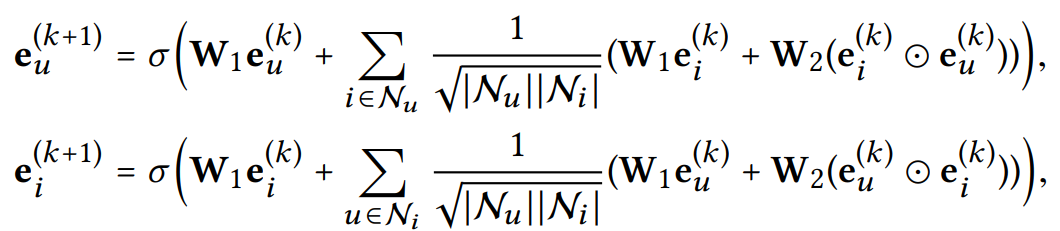
user(u) item(i)

• self-connection $(W_1e_u^{(k)},W_2e_i^{(k)})$을 통해 이전에 갖고 있었던 임베딩 정보 유지
• 각 레이어 연산 결과에 symmetric normalization $\frac{1}{\sqrt{|N_u||N_i|}}$을 적용하여 정규화
• feature transformation$(W_1,W_2)$과 nonlinear activation(σ)를 사용해 임베딩 값 업데이트

NGCF는 user-item interaction matrix를 투입했을 때 L개의 레이어를 통과하여 L+1개의 임베딩 user : $(e_u^0, e_u^1, ... ,e_u^L)$ | item : $(e_i^0, e_i^1, ... ,e_i^L)$를 얻을 수 있으며, L+1개의 임베딩을 연결하여 최종 user 임베딩과 item 임베딩을 얻을 수 있고 내적을 사용해서 prediction score 생성함.

Empirical Explorations on NGCF

NGCF-f : feature transformation matrices $W_1, W_2$ 제거
NGCF-n : non-linear activation function σ 제거
NGCF-fn : feature transformation matrices, non-linear activation function 둘다 제거

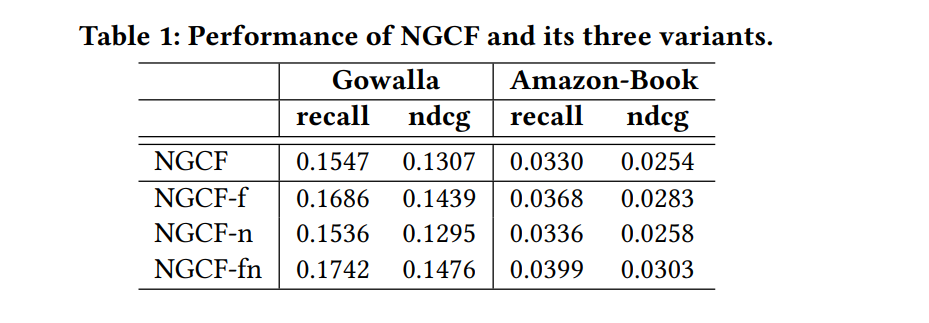
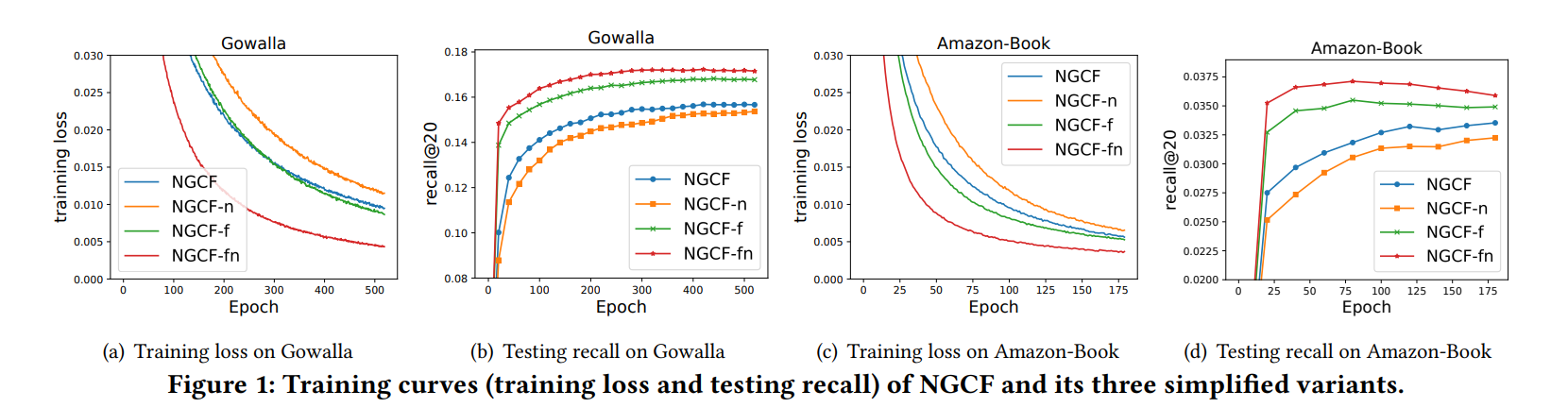
❶ feature transformation을 추가하는 것은 NGCF에 부정적인 영향을 미침. feature transformation을 제거함으로써 NGCF와 NGCF-n의 성능이 크게 향상됨.
❷ non-linear activation을 추가하는 것은 feature transformation이 포함된 경우 약간 영향을 미치지만, feature transformation을 비활성화할 때 부정적인 영향을 미침.
❸ 전반적으로, feature transformation과 non-linear activation는 NGCF에 부정적인 영향을 미침. 둘다 제거한 NGCF-fn이 NGCF에 비해 큰 개선을 보임. (recall 기준 9.57% 개선)

METHOD

LightGCN

GCN의 핵심 아이디어는 그래프 상의 노드를 표현하기 위해 이웃 노드의 정보를 결합하는 것. 이를 위해 GCN은 graph convolution을 반복하여 각 노드의 새로운 표현을 만듦.

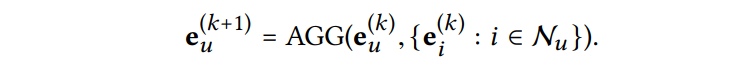
대부분의 작업에서는 feature transformation 또는 nonlinear activation을 AGG 함수와 결합함. semantic input feature를 가지는 graph classification task에서는 잘 수행되지만, CF에서는 아닐 수 있음!

➡ 계속 얘기한 nonlinear activation과 feature transformation을 제거하고 neighborhood aggregation만 남겨놓은 구조

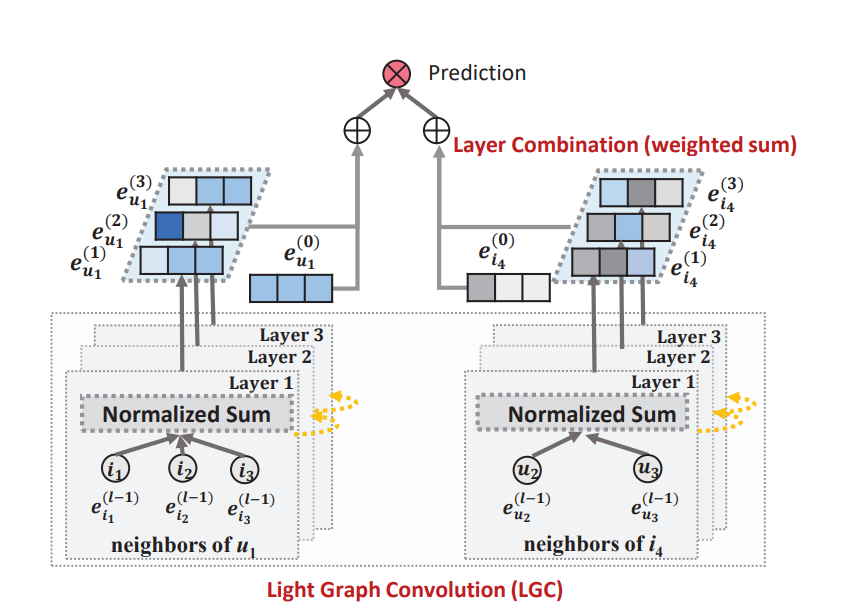
LGC(Light Graph Convolution)에서는 연결된 이웃만 aggregate하고 self-connection을 하지 않음. Layer Combination에서의 작업이 self-connection의 효과와 동일해서 제외함.

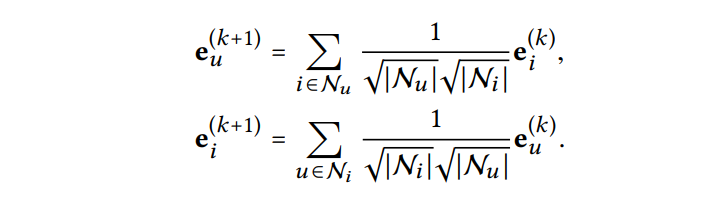
기존에 GCN에서 사용하는 정규화 방식인 symmetric normalization $\frac{1}{\sqrt{|N_u||N_i|}}$을 그대로 사용
➡ embedding의 크기가 증가하는 것을 막을 수 있음.

위의 식을 이용해서 더 높은 레이어의 임베딩을 계산할 수 있으므로 유일하게 학습 가능한 파라미터는 0번째 레이어의 임베딩뿐..!
K개의 레이어를 LGC한 후에 각 레이어에서 얻은 임베딩을 결합하여 최종 표현을 생성함.

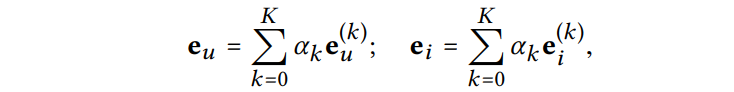
$α_k$ ≥ 0은 최종 임베딩을 구성하는 k번째 레이어의 임베딩의 중요도
일반적으로 $α_k$를 균일하게 1/(K + 1)로 설정하는 것이 좋은 성능을 낸다는 것을 발견함. ➡ LightGCN을 복잡하게 만들지 않기 위해 특별한 설정없이 이대로 사용

📍 최종 표현을 얻기 위해 레이어 결합을 수행하는 이유

(1) 레이어의 수가 증가함에 따라 임베딩이 over-smoothed될 수 있기 때문
(2) 서로 다른 레이어의 임베딩은 서로 다른 의미를 포착하기 때문
(3) 가중합을 사용하여 서로 다른 레이어의 임베딩을 결합하면 self-connection을 가진 graph convolution의 효과를 가질 수 있음

💡 레이어 수가 증가함에 따라 임베딩이 over-smoothed 되는 이유 + 레이어 결합으로 이 문제를 해결할 수 있는 이유
GCN은 그래프에서 이웃 노드의 정보를 aggregate하여 각 노드의 표현을 갱신함. 이 과정을 여러 번 반복하면 각 노드의 표현이 점점 변화하는데 너무 많은 레이어를 거치면 노드의 표현이 "over-smoothed"될 수 있음. 즉, 각 노드의 표현이 너무 유사해져서 그래프 상의 구조나 특성을 더 이상 충분히 반영하지 못하게 됨. 이는 임베딩이 너무 많은 정보를 잃어버리고 더 이상 유의미한 패턴을 학습하지 못하게 될 수 있다는 것을 의미함.
여러 레이어에서 얻은 임베딩을 결합하면 각 레이어에서 포착한 서로 다른 의미와 특성을 종합적으로 반영할 수 있음!

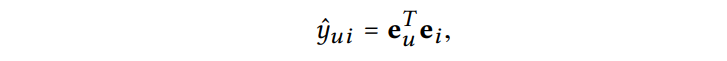
모델 예측은 user와 item의 최종 표현의 내적으로 정의됨. 추천을 위한 ranking score로 사용

Matrix에 대해 논문에서 설명할 때 대부분 기본적인 설명을 해주는데 기억해야 할 몇 가지 중요한 부분이 있다❗

✅ user 개수가 M, item 개수가 N이지만, Matrix가 (MxN)이라는 것이 아니라 (M+N) x (M+N)이다!
✅ $A$ Matrix를 보면, 빠르게 이해할 수 있는데, 0이 두 군데에 존재한다. 즉, user-item interaction만 반영되고 user-user, item-item interaction은 반영되지 않는다. 그래서 0으로 나타나있는 것이다!

Model Analysis

📍 LightGCN은 self-connection을 사용 ❌

왜 LGC에서 self-connection을 제거해도 되는지 수식적으로 설명

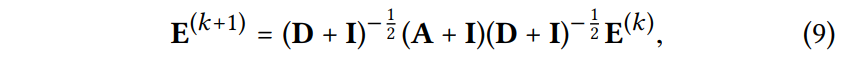
SGCN (Simplifying Graph Convolutional Networks)의 수식을 보면 알 수 있듯, $I ∈ R^{(M+N)×(M+N)}$를 더해줘서 self-connection을 유지함.

LightGCN에서는 단순화를 위해 $(D + I)^{−\frac{1}{2}}$을 제거
➡ 아래 식이 만들어짐

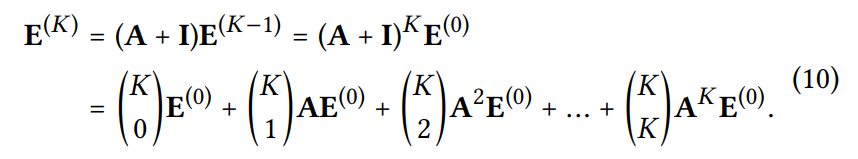
$α$를 조정하면 아래 식과 동일하다는 것을 알 수 있음
➡ self-connection 수식을 굳이 넣지 않더라도 self-connection의 효과가 있음

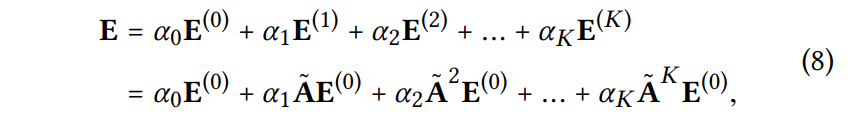
📍 APPNP에서 입증된 over-smooting을 잘 다루는 LightGCN
APPNP는 initial embedding을 더해줌으로써 long range에서도 oversmoothing에 강한 모델임.

over-smoothing은 레이어의 수가 증가할 수록 최종 임베딩 값이 유사해져 더 이상 유용한 정보를 추출할 수 없게 되어 모델의 성능이 저하되는 문제를 말함.

➡ APPNP의 propagation layer 식

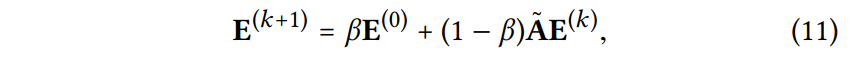
• k 번째 임베딩 $E^{(k)}$을 구하기 위해 초기 임베딩 $E^{(0)}$값을 더해 줌으로써 over-smoothing 문제를 해결
• $β$ ($E^{(0)}$의 반영 비율을 나타내는 확률변수)를 통해 초기 임베딩 값에 대한 영향력을 조정 가능

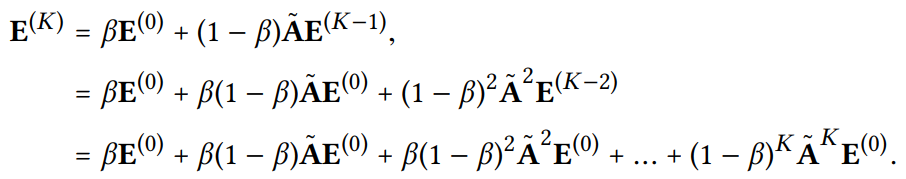
📍 두 개의 레이어를 가진 LGC 분석
user(item)와 연결된 다른 user(item)의 second-order layer 분석하여 인사이트를 얻고자 함.

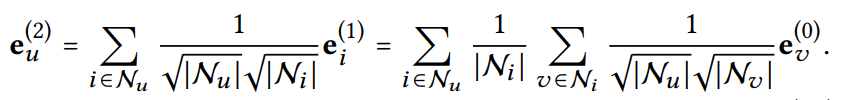
user $v$가 target user $u$와 같은 item에 상호 작용했다면, 사용자 $v$의 $u$에 대한 영향은 $c_{v→u}$계수에 의해 측정 가능

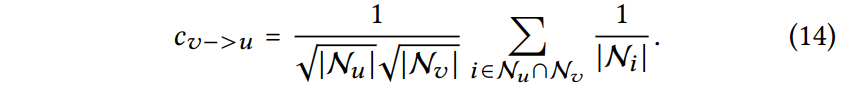
• 두 user의 interaction history간 겹치는 item이 많으면 계수🔺
• 겹치는 item이 인기가 많으면 계수🔻 (연결이 적으면 계수🔺)
• user $v$의 action history가 적으면 계수🔻 (유저 $u$와 연결된 $v$가 적을수록)
  
  

Model Training

LightGCN의 학습 가능한 파라미터는 0번째 레이어의 임베딩에만 존재
손실함수 Bayesian Personalized Ranking (BPR) 사용

BPR
선호하는 아이템에 대한 예측값이 나머지보다 높도록 유도하는 pair-wise optimization 기법

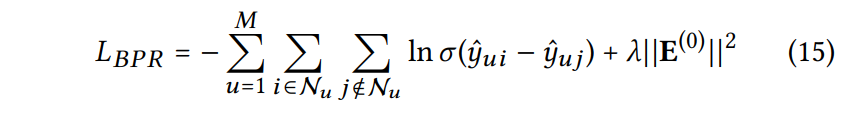
i : user가 선호하는 item (구매한 item)
j : user가 선호하지 않는 item (구매하지 않은 item)

• 모든 유저에 대해서 실제 구매한 아이템과 구매하지 않은 아이템의 차이를 계산
• 구매한 item에는 높은 가중치를 부여하고 구매하지 않은 item은 낮은 가중치를 부여해 loss를 계산하여(BPR 사용) 모델 최적화

EXPERIMENTS

기존 NGCF 모델과 성능 비교

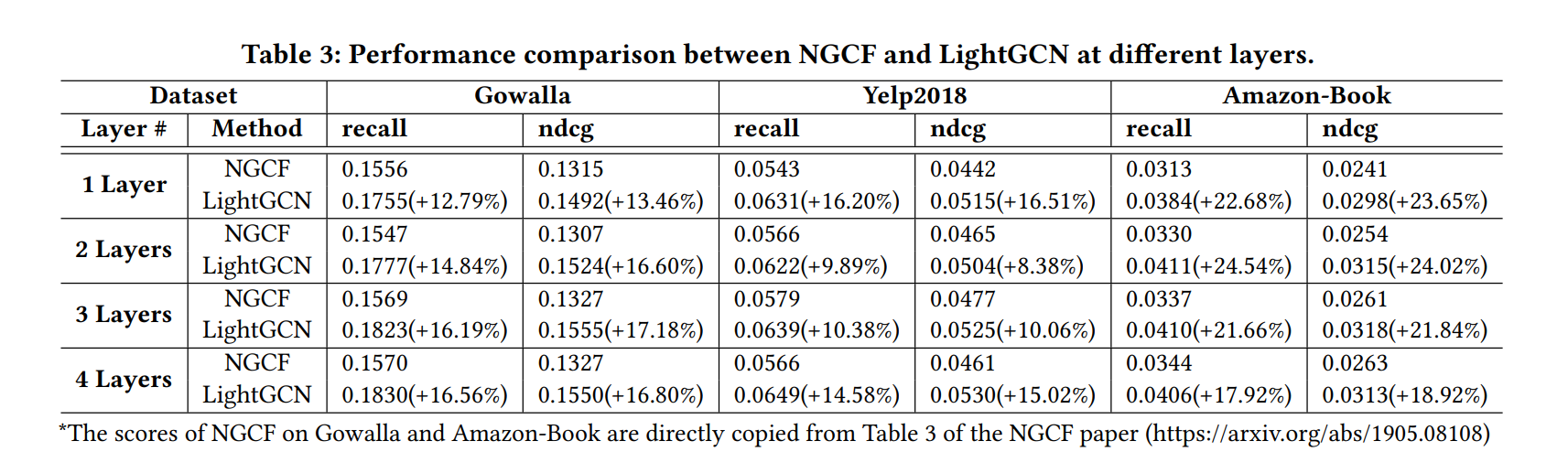
평가 지표로 recall과 ndcg를 보았을 때 모든 데이터 셋과 레이어 수에서 LightGCN의 성능이 훨씬 우수함.

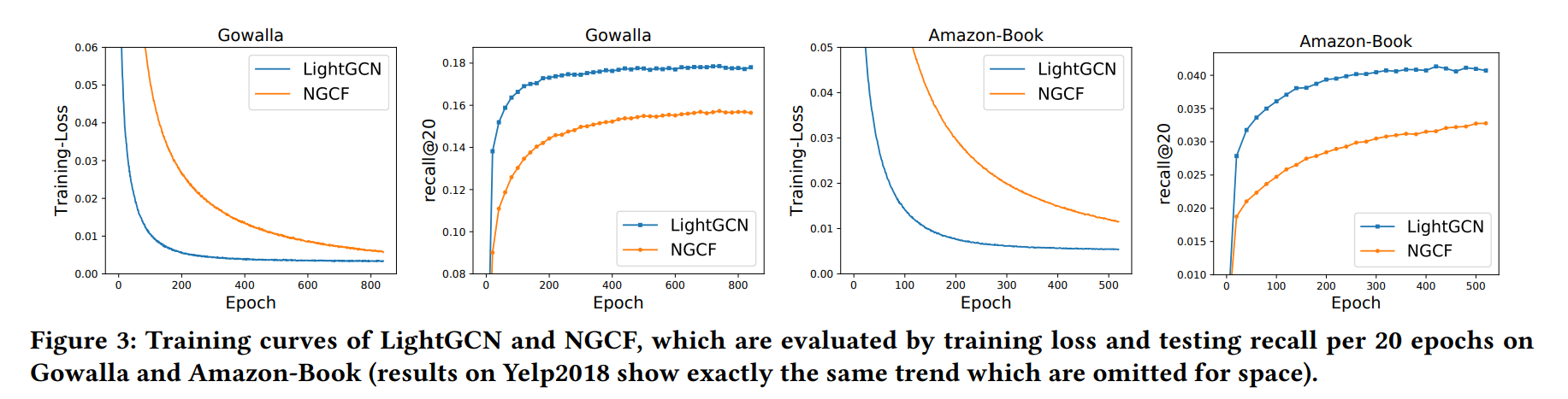
Loss를 보게 되면 LightGCN의 Loss가 더 낮은 것을 보아 NGCF 모델보다 학습을 더 잘함.

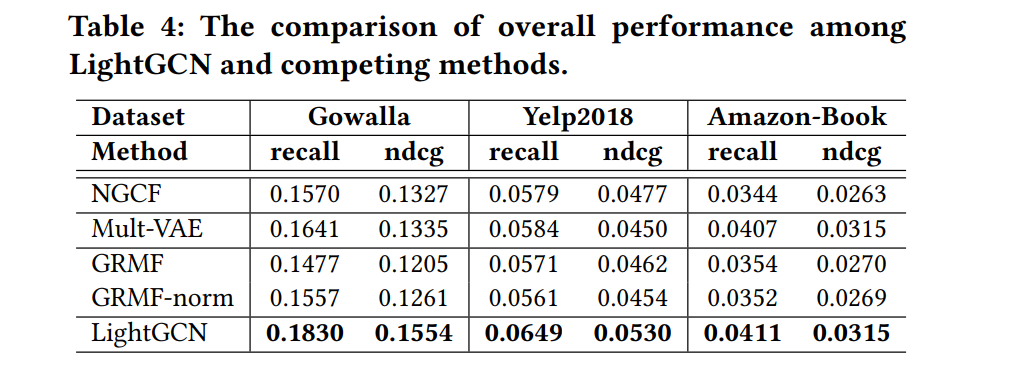
최신 SOTA모델들과 비교

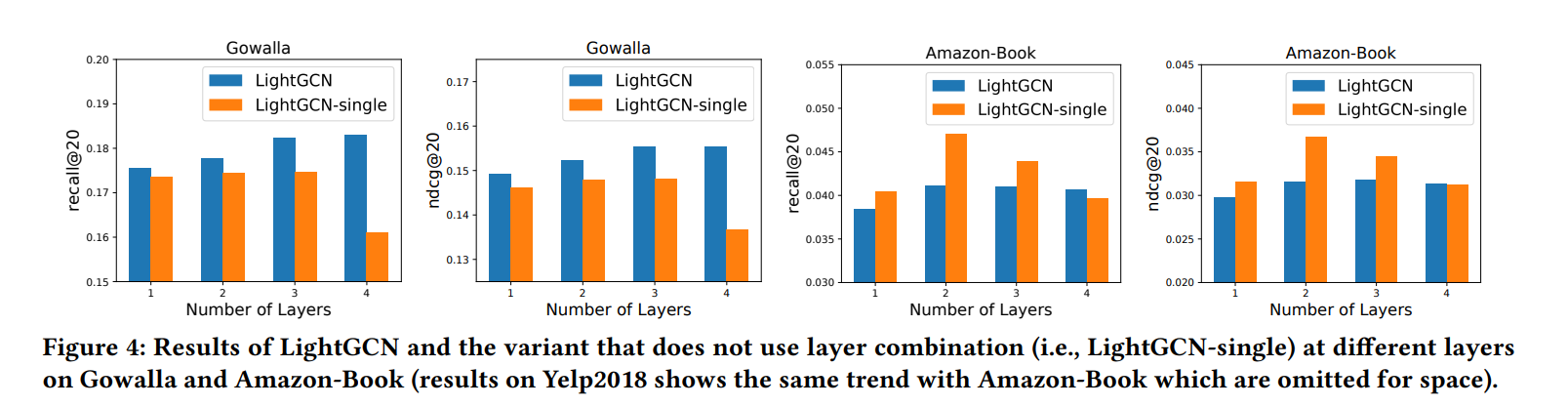
LightGCN-single에서 (주황색 막대) Layers의 수가 증가할수록 모델의 성능이 떨어지는 것을 보아, over-smoothing이 발생했다고 판단
➡ 파란색 막대 - Layer combination의 효과로 over-smoothing 문제 해결