
Review - Linear Regression
model
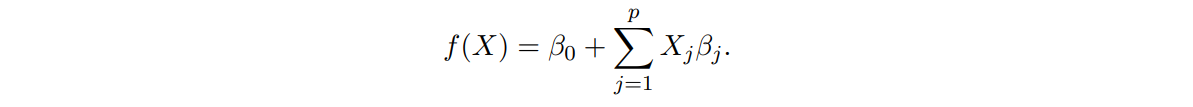
- 일반적으로 parameter β를 추정하기 위한 학습데이터 집합 (, ), ... ,(, )를 가짐
- 선형 회귀 모델은 inputs이 , ... ,일 때 의 함수를 추정하는 것
Estimation
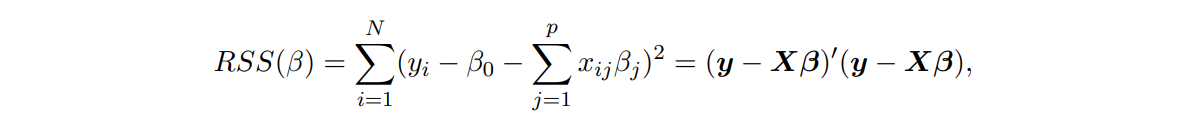
추정 방법은 RSS를 최소로 만드는 β를 구하는 것
( 는 matrix, β = (, ... , , 는 vector )
📌 X가 p+1인 이유는 intercept까지 포함되기 때문
📌 p는 #feature, N은 #observation
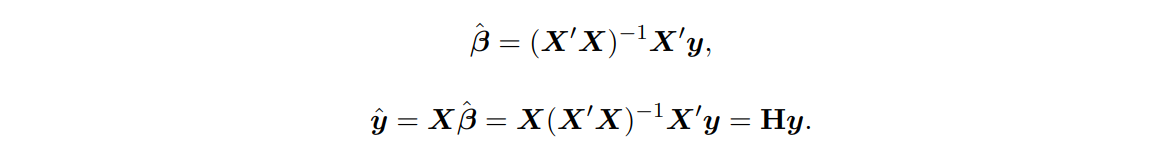
❓만약 가 선형 독립이 아니라서 가 full rank가 아니라면
➡ 가 singular이 되고, least squares coefficients 가 명확하게 정의되지 않을 수 있음.
➡ 특이값 분해(Singular Value Decomposition, SVD) 등의 기술 사용
Inference
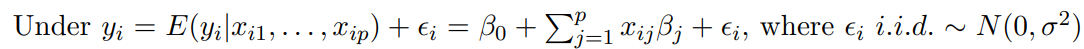
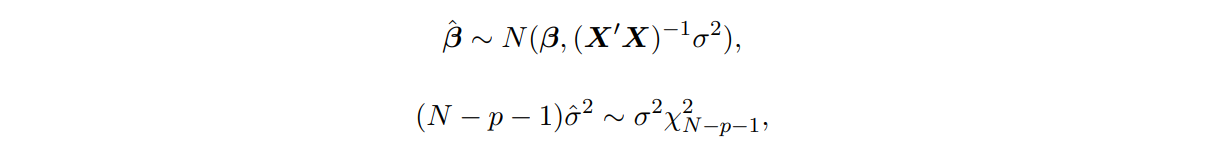
📌 와 은 통계적으로 독립
To test : )
사용 (는 (의 번쨰 diagonal element)
Under , ~
x 100% CI of :
To test :
use
는 개의 파라미터를 갖는 큰 모델의 RSS이고, 는 개의 파라미터를 갖는 작은 모델의 RSS임.
Under , ~
✔ F distribution은 2개의 ratio로 이루어짐
> 0 ➡ F distribution도 항상 > 0 ➡
❓왜 항상 이 보다 클까
➡ 은 simple model, 은 complex model로 에서 일부 parameter를 0으로 둔 것이 이 됨.
➡ simple model의 RSS > complex model의 RSS
The Gauss-Markov Theorem
parameter β에 대한 least squares estimate(최소 제곱 추정치)는 모든 linear unbiased estimates 중에서 분산이 가장 작은 값임
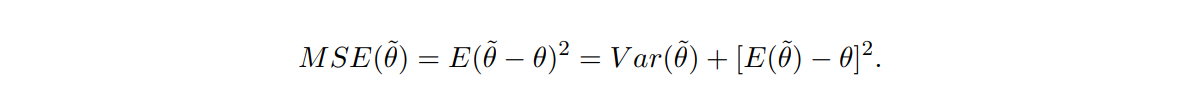
biased estimator에 더 작은 MSE(Mean Squared Error)가 존재할 수 있음
➡ 약간의 bias를 감수하고 variance의 큰 감소시키는 효과를 가질 수 있음
➡ least squares coefficients의 일부를 줄이거나 0로 설정하여 biased estiamte로 만들 수 있음. (variable selection & ridge regression)
💡 쉽게 말하면, bias가 없는 estimator(unbiased estimator) 중에 variance가 가장 작은 것을 찾는 것이 Gauss-Markov Theorem인데, bias가 있는 것 중(biased estimator)에 variance가 굉장히 작아서 총 MSE가 bias가 없는 것보다 더 작은 식이 있을 수 있음
➡ 우리는 작은 MSE를 찾는 것이 목표이기 때문에, bias가 있지만 variance가 작아서 총 MSE 값을 더 작게 가질 수 있다면, biased estimator를 선택할 수 있음.
Comparison of Linear regression with KNN
KNN은 Regression과 Classification 두 가지로 쓰이는데, 이 부분에서는 Regression 측면에서만 보도록 하겠음
KNN regression
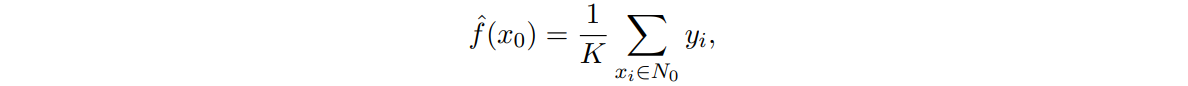
: 와 가까운 개의 training observation
c.f. KNN Classifier
| 1 | A | ||
| ... | ... | ... | B |
| ... | ... | ... | O |
| 100 | ... | ... | A |
간단하게 예시를 들자면, 와 가까운 k개의 데이터를 찾는 것
➡ A형과 비교 ➡ A형인 observation 수 / k
와 같이 B형, O형, AB형 모두 구한 뒤, 가장 큰 확률이 나오는 class로 분류
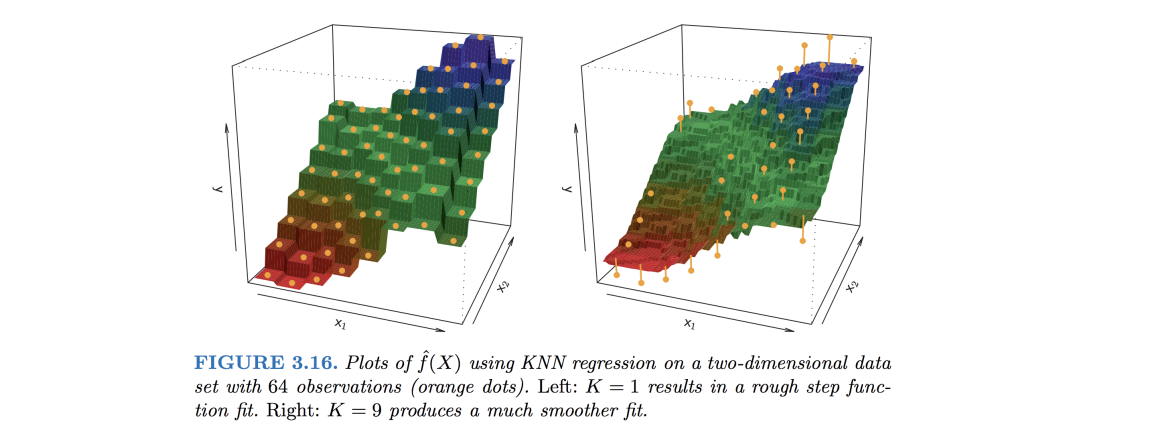
왼쪽 그림이 K=1일 때이고, 오른쪽 그림이 K=9일 때 + 주황색 dots는 observations
왼쪽 그림은 wiggly하고 오른쪽 그림은 smooth한데, K가 작으면 값들의 분포가 크고 K가 크면 값들의 분포가 크지 않아서 smooth 해짐
📌 wiggly ➡ 🔺, 🔻
📌 smooth ➡ 🔻, 🔺
- true form이 linear할 경우
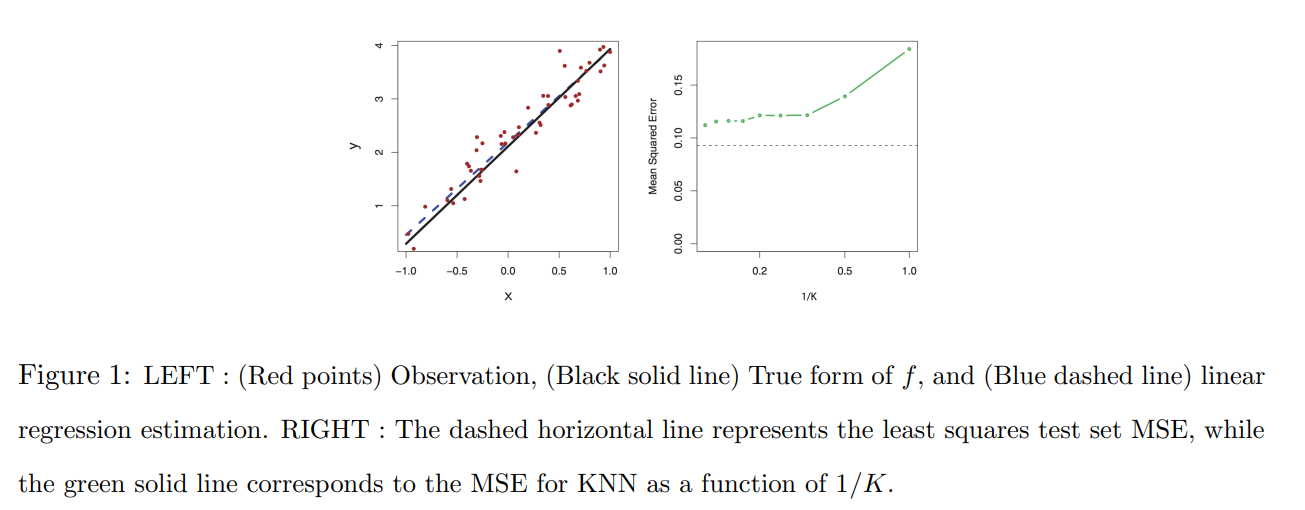
OLS는 K값의 변화에 따라 변화하지 않고, KNN은 K값의 변화에 따라 달라짐.
➡ 위 그래프에서는 OLS의 MSE가 더 낮으므로 OLS가 더 좋음.
- true form이 linear하지 않을 경우
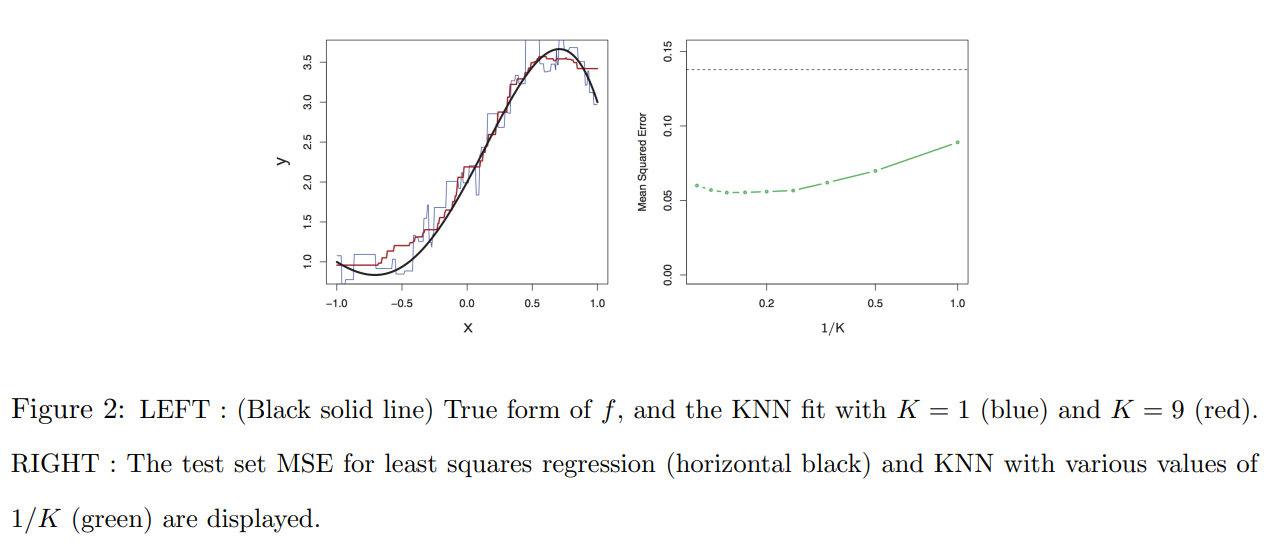
➡ 위 그래프에서는 KNN의 MSE가 OLS의 MSE보다 더 낮으므로 KNN이 더 좋음.
- Curse of dimensionality in KNN
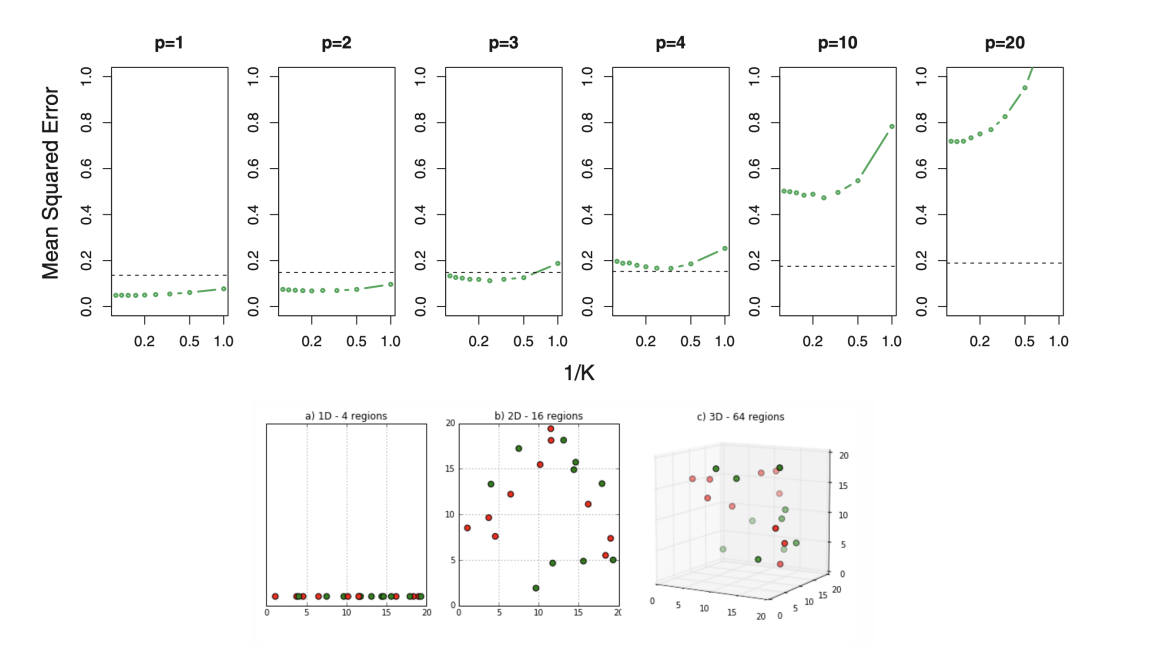
➡ dimension이 증가할수록 KNN의 성능🔻
reference - Introduction to Statistical Learning

감사합니다. 이런 정보를 나눠주셔서 좋아요.