Resampling Method

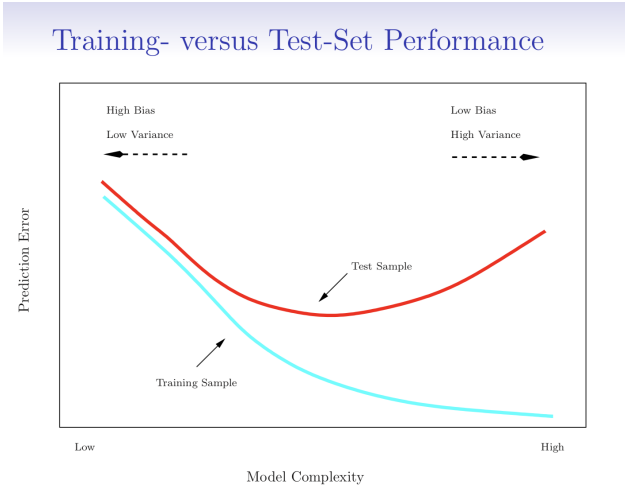
Cross-Validation

• statistical learning method를 사용할 때, 주어진 데이터 셋에서 test error가 작게 나오면 해당 방법을 사용하는 것이 타당하다고 할 수 있음.
• test error는 특정 test set이 있을 경우 쉽게 계산할 수 있지만, 대부분 그렇지 않음.
  ➡ available training data를 사용하여 quantity를 추정하기 위해 많은 기술이 사용됨.

📌 일부 훈련 데이터를 테스트에 사용하여 test error를 추정하는 방법에 대해 다룸.

The Validation Set Approach

• random하게 training set과 validation (or hold-out set)으로 나눔.
• training set으로 model fitting + fitted model로 validation set을 예측
• validation set error는 test error를 제공함
  ➡ quatitive response - MSE
  ➡ qualitative response - misclassification rate

+ 모델 평가를 위해 일부 데이터를 사용하므로 결과가 data split에 따라 달라질 수 있음

training set의 일부를 모델을 평가하기 위한 validation set으로 split하여 사용

K-fold Cross-validation

• 데이터를 K개로 나눔 (각 부분의 크기는 같음)
• (K-1) parts는 training set로 사용 + 나머지 1개의 part는 validation set으로 사용
• K번 반복 ➡ K개의 결과의 평균 사용
  

$MSE_k =\displaystyle\sum_{i\in C_k}{(y_i-\widehat{y}_i^{(k)})^2}/n_k$
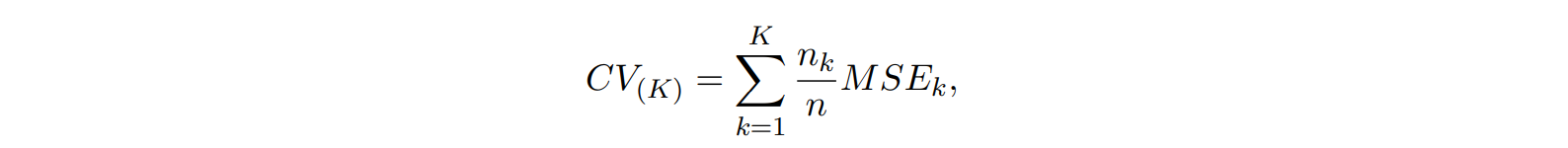
$\widehat{y}_i^{(k)}$ : k번째 fold를 제외하고 modeling한 모델에 $x_i$를 넣어서 얻은 값

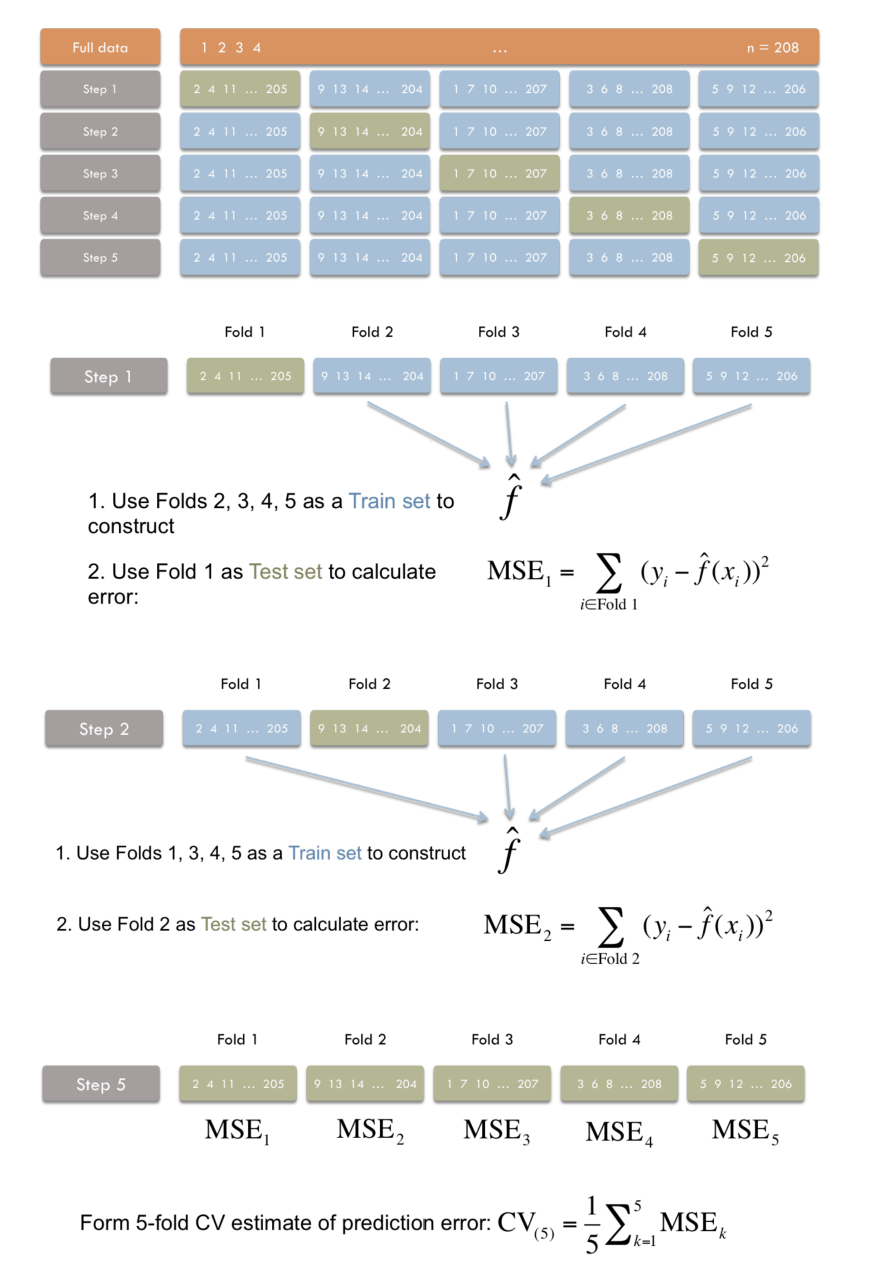
📌 overlap 되는 부분이 없음 (Bootstrap은 overlap 존재)

✔ LOOCV (Leave-one out CV)
$K=n$일 경우 각 반복에서 하나의 데이터 포인트만을 validation set로 사용하고 나머지 데이터를 training에 사용
📌 bias는 작지만, 시간이 굉장히 많이 소요됨

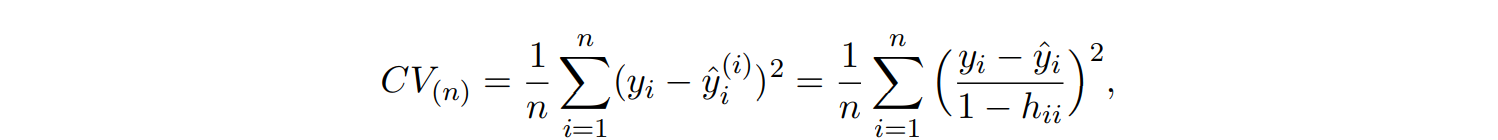
least squares linear or polynomial regression에서 LOOCV를 구현하는 데 cost를 많이 줄일 수 있고, single model fit의 cost와 동일해짐
💡 오른쪽 식을 보면 n times를 반복해서 얻은 값이 아닌 n 개의 데이터를 가지고 얻어진 값을 사용하여 1 time의 시간이 걸림을 알 수 있음.

$K=5$ or $10$이 bias-variance tradeoff에 있어 좋은 결과를 제공

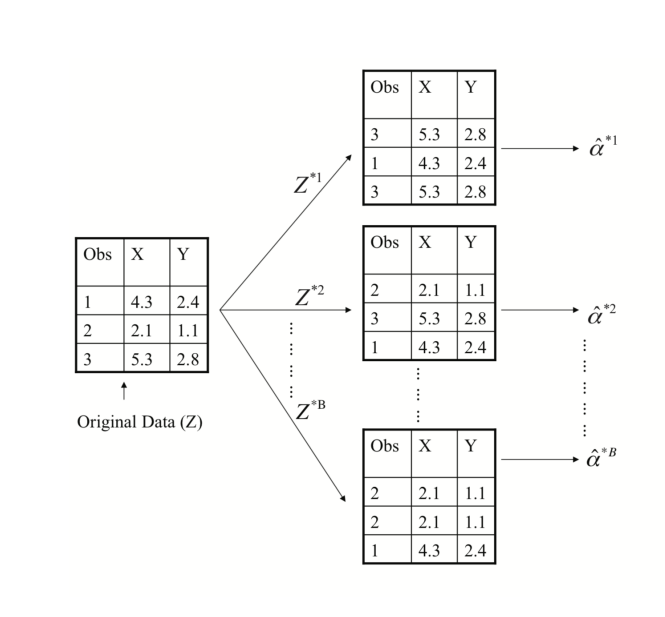
The Bootstrap

• 실제 데이터에서는 원래 모집단에서 새로운 sample을 생성할 수 없음.
• bootstrap에서는 독립적인 데이터 세트를 반복적으로 얻는 대신, 원래 데이터 세트에서 observation을 복원추출(replacement)하여 중복을 허용하는 방식으로 함.
  ➡ "bootstrap data sets"

📌 overlap되는 것이 특징

estimate test MSE

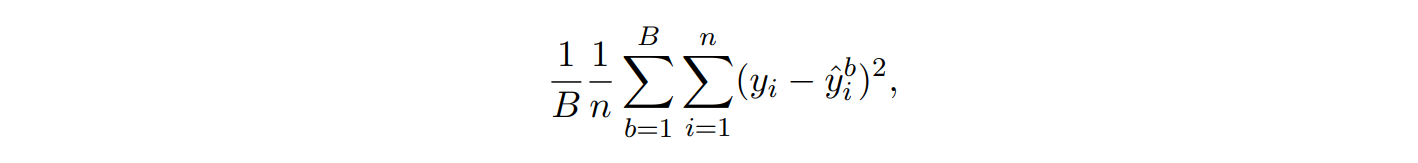
prob $i$th obs is "not" selected when you sample one data for constructing bootstrap sample b
$= 1 - \frac{1}{n}$

➡ prob $i$th obs is "not" selected when you sample n times data for constructing bootstrap samble b
$= 1 - (\frac{1}{n})^n$

➡ prob $i$th obs is selected when you construct bootstrap sample b
$= 1 - (1 - \frac{1}{n})^n$

$\lim_{n \to \infty} 1 - (1 - \frac{1}{n})^n \approx 1 - \frac{1}{e} = 0.632$

---

reference - Introduction to Statistical Learning