Moving Beyond Linearity

linearity assumption은 가정일 뿐, 언제나 선형 모형을 따를 수는 없습니다. 따라서 이번 챕터에서는 항을 추가하거나, transformation을 함으로써 비선형성을 따르는 모형들을 살펴보고자 합니다.

Polynomial Regression

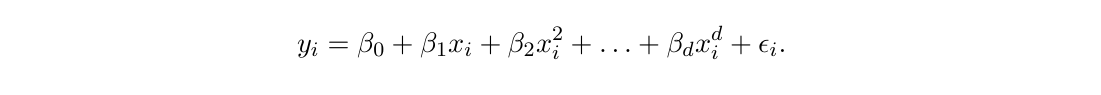
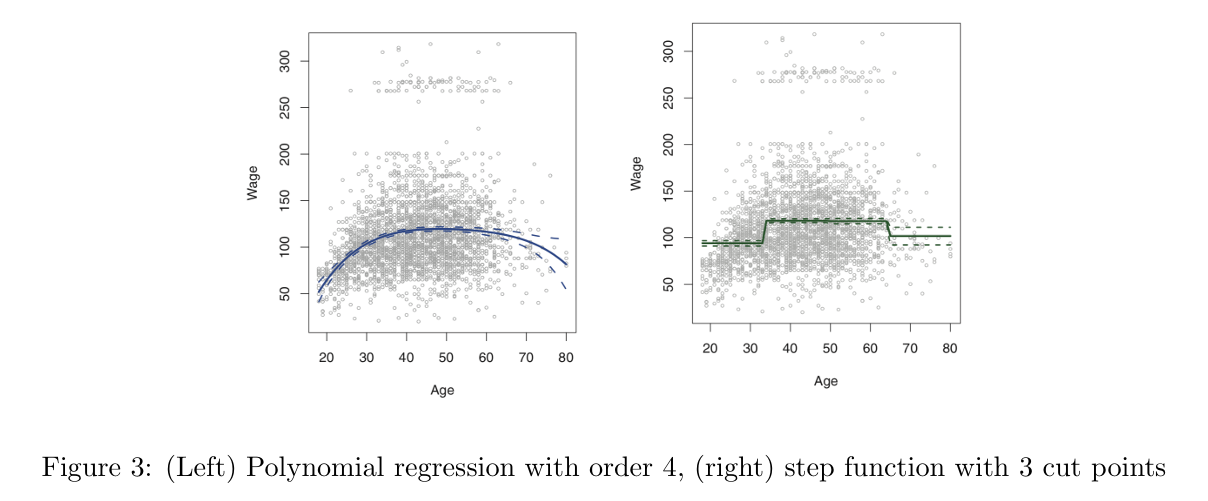
종속변수와 독립변수가 선형을 따르지 않을 경우 단순 선형회귀 모형을 적용하게 되면, 적합하지 않을 수 있습니다. 다항 회귀는 비선형 곡선을 생성할 수 있게 해주어 한계점을 극복할 수 있습니다.

Step Functions

X의 범위에 따라 구간별로 다른 상수를 fitting하는 것을 Piecewise polynomial이라고 합니다.
이때 구간별로 나누는 point들을 knots 또는 cut off point라고 부릅니다. constant가 바뀌는 곳에서 cut off를 찾으면 되고, cut off를 통해 더 적은 차수를 사용할 수 있게 되어 더 간단한 식으로 fitting 할 수 있습니다. 밑에 식에 적용하면 $c_1, c_2, ... , c_k$가 cutpoints가 됩니다.

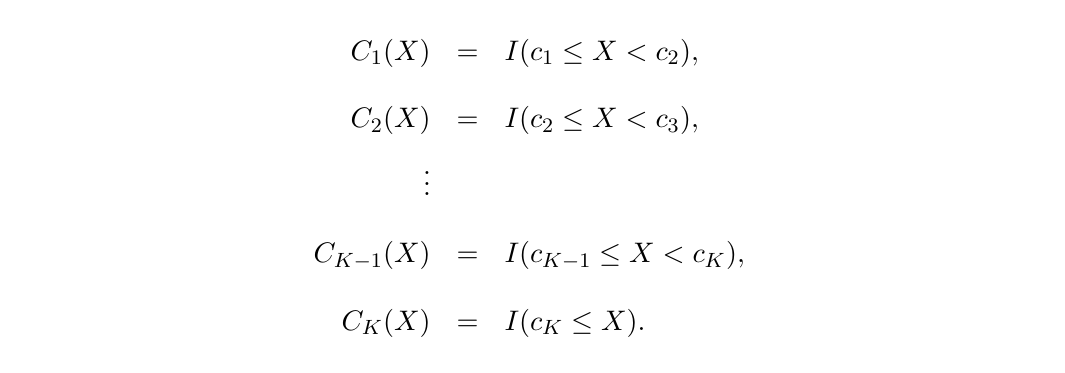
🔼 선형 모델에 fitting 시킨 식

Regression Splines

Piecewise Polynomials

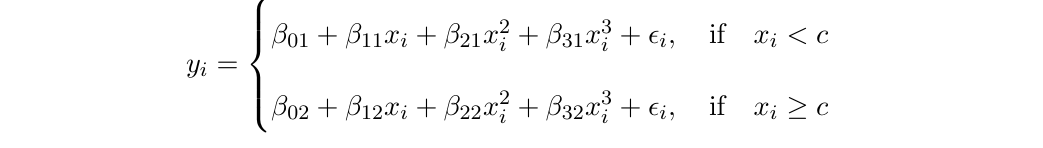
X의 전체 범위에 high-degree의 다항식을 fitting시키는 대신, piecewise polynomial는 X의 범위를 range에 따라 나누어 고차항의 식을 저차원으로 fitting 시킵니다.

Regression Splines

Piecewise polynomial의 경우 knot에서 continuous하지 않습니다. Regression Spline은 knot에서 연속이라는 조건을 추가하여 다항식을 fitting하는 것입니다.

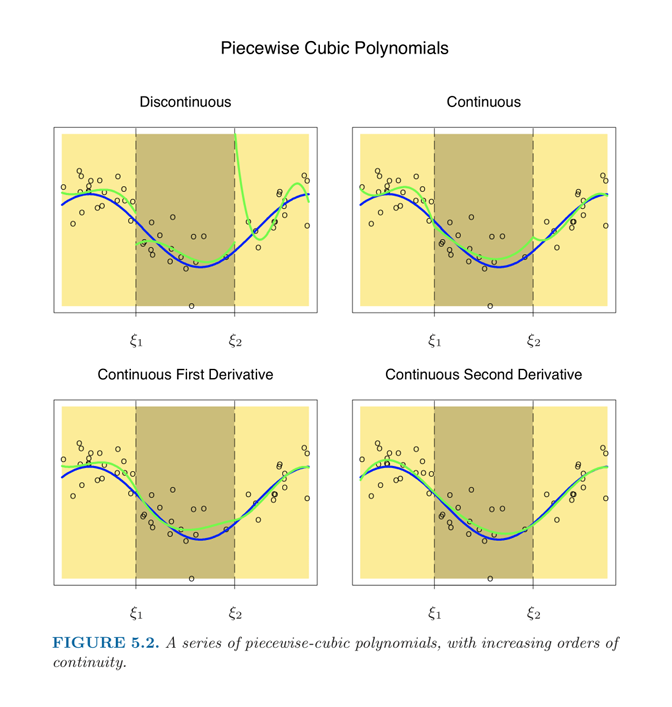
🔼 파란색 선은 underline, 초록색 선은 model fitting의 결과, dot은 observation

첫 번째에서 두 번째 그림으로 갈 때는 continuity assumption을 적용한 것입니다. 따라서 Discontionous 했던 그래프가 Continuous하게 바뀌게 되었죠. 그런데 미분불가능한 peak point가 있어 미분한 그래프가 discontinous하게 됩니다.
세 번째 그림으로 넘어가 미분한 curve가 연속이 되도록 합니다. 이 미분하는 과정을 반복하게 됩니다.

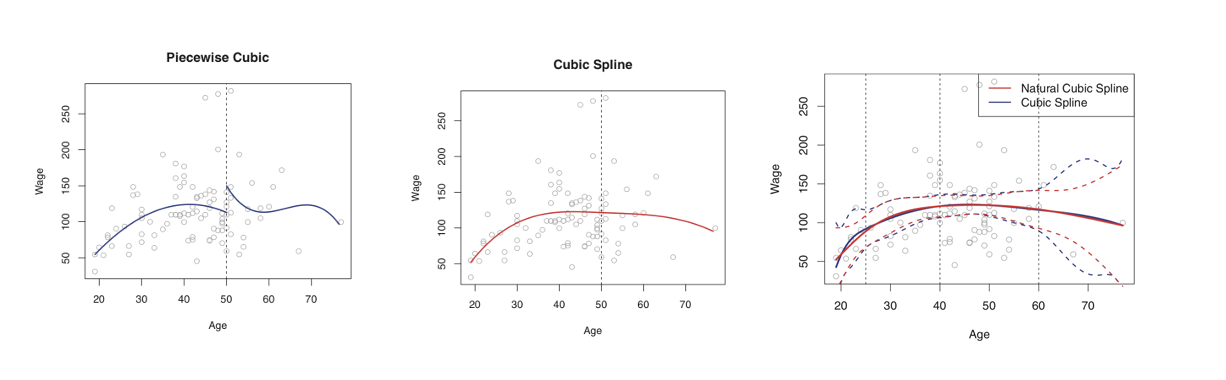
세 번째 그래프에서 Cubic Spline은 Age가 커질수록 CI가 넓은 것을 확인할 수 있습니다. 더 좁은 CI를 위해 Natural cubic spline을 적용한 것이 빨간색 선입니다.

The Spline Basis Representation

K개의 knot를 가진 cubic spline에서 우리는 intercept 와 $3+k$ predictors로 least squares regression을 해야 합니다. $X,X^2,X^3,h(X,ξ_1),...,h(X,ξ_K)$의 form을 사용하게 되는데
$h(x,ξ) = (x −ξ)^3_+$ 과 같습니다. (total of K + 4 regression coefficients.)

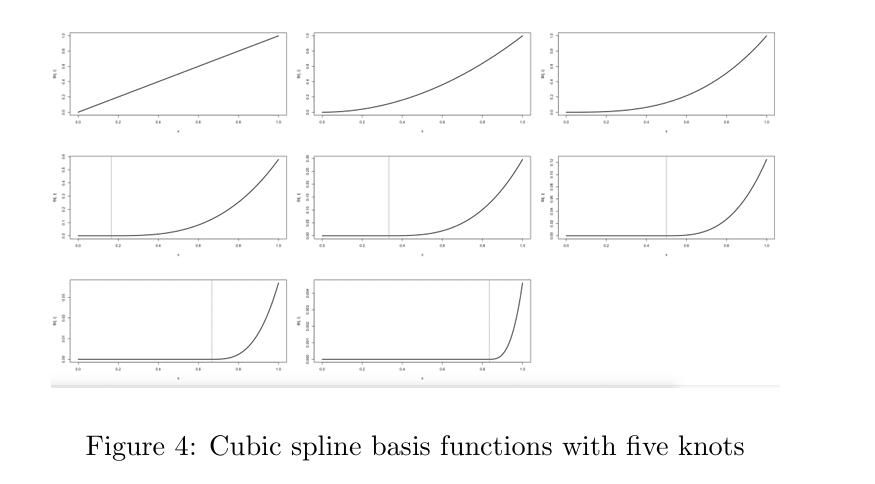
natural spline은 가장 작은 knot보다 작은 region과 가장 큰 knot보다 큰 region은 cubic이 아니라 linear하게 적합하는 제약 조건을 추가한 모형을 말합니다.

Smoothing Splines

smoothing spline은 주어진 input의 unique한 모든 값을 knots로 사용합니다. 따라서 Smoothing spline을 구현하는 것은 모든 unique한 X값을 knots로 사용하는 Natural Cublic Spline을 구현한 것과 같습니다.

$RSS = \sum_{i}(y_i - g(x_i))^2$ 일 때 우리는 RSS를 작게 만들기를 바랍니다.

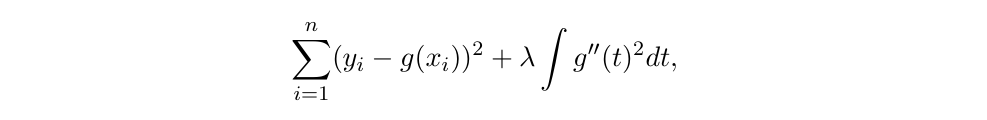
$\lambda$가 0이면 OLS fitting과 같게 되고, $\lambda$가 커질수록 g는 더 smooth해집니다. 여기서 $\lambda$를 조절함에 따라 bias, variance trade-off가 나타나게 됩니다.

Local regression

local regression은 전체 데이터를 사용하지 않고 local한 data를 사용하는 동시에 그 local 안에서도 다른 weight를 적용하는 방법론입니다.

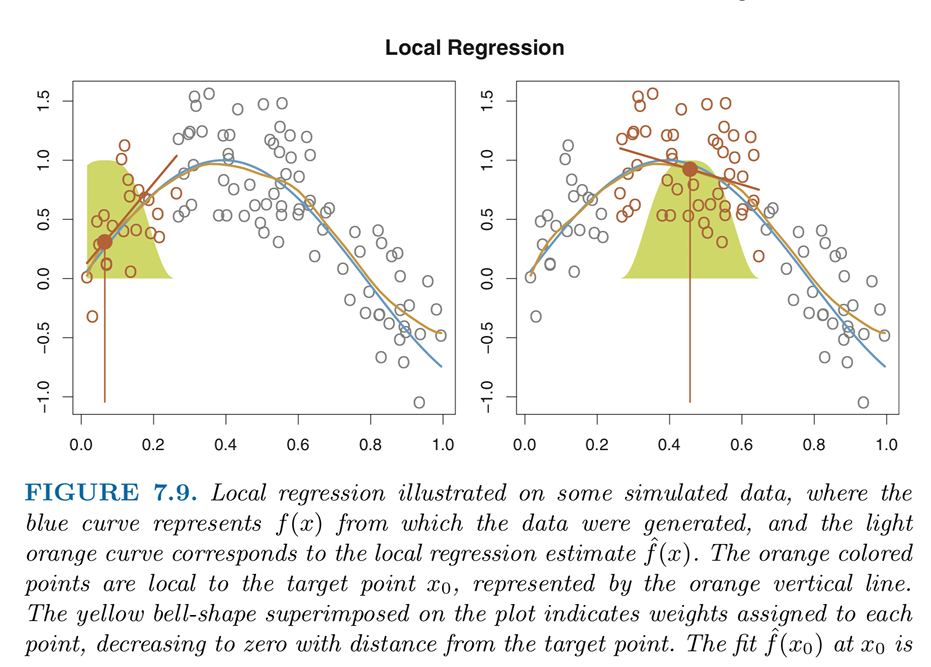
그래프를 통해 자세히 설명하자면, 각 point마다 다른 weight를 가지게 되는데 이때 target point와 가깝다면 weight값이 올라가고, 멀어지면 weight값이 내려가게 됩니다. 선택되지 않은 점들은 weight가 0이 되는 것입니다.

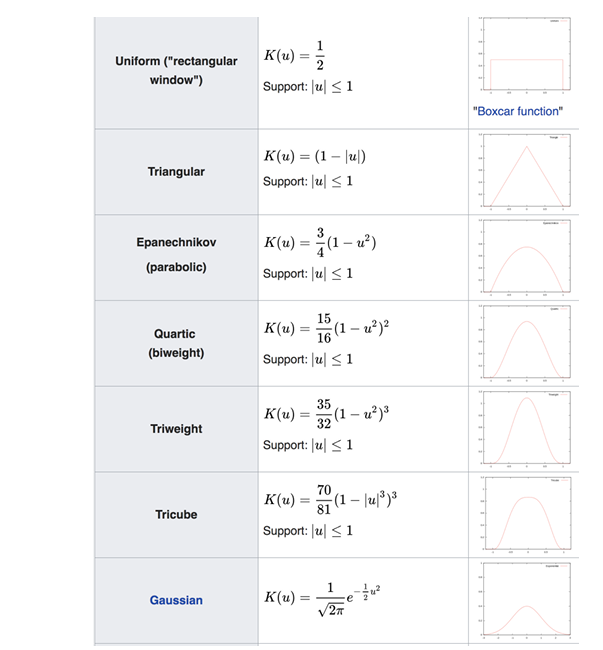
다음과 같이 다양한 weight function이 있지만, weight ftn에 따라 크게 달라지지는 않습니다.

local regression의 장점은 모든 data에 fit한 function을 요구하지 않는다는 것고 단점은 다른 method들에 비해 data point가 많아야 한다는 것입니다. 이는 특히 dimension이 커질수록 많이 필요하게 됩니다.

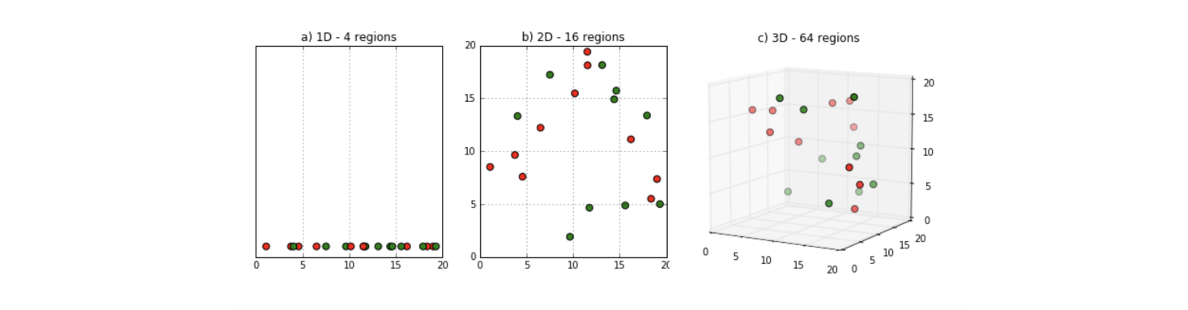
같은 data point인데도 불구하고 dimension에 따라 달라지는 것을 볼 수 있는데, 1D에서는 촘촘하지만 dimension이 커질수록 같은 데이터 개수라도 sparse해지는 것을 확인할 수 있습니다 그래서 dimension이 커질수록 데이터의 개수가 많이 필요하게 됩니다.

Generalized Additive Models

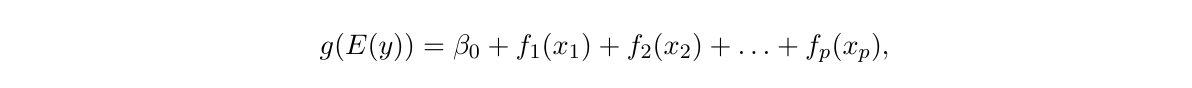
GAMs는 standard linear model을 각 variable의 비선형 함수들을 통해 확장한 것을 말합니다. normal dstn을 따르지 않을 때, link ftn을 사용하는 것입니다.

GLM의 대표적인 예시인 Logistic regression의 경우 link function은 다음과 같은 형태를 가집니다.

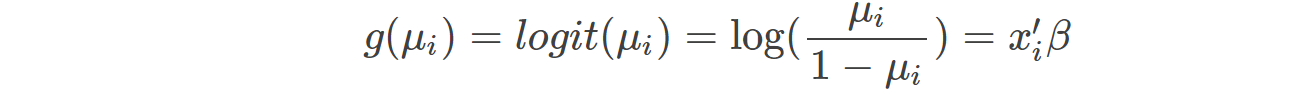
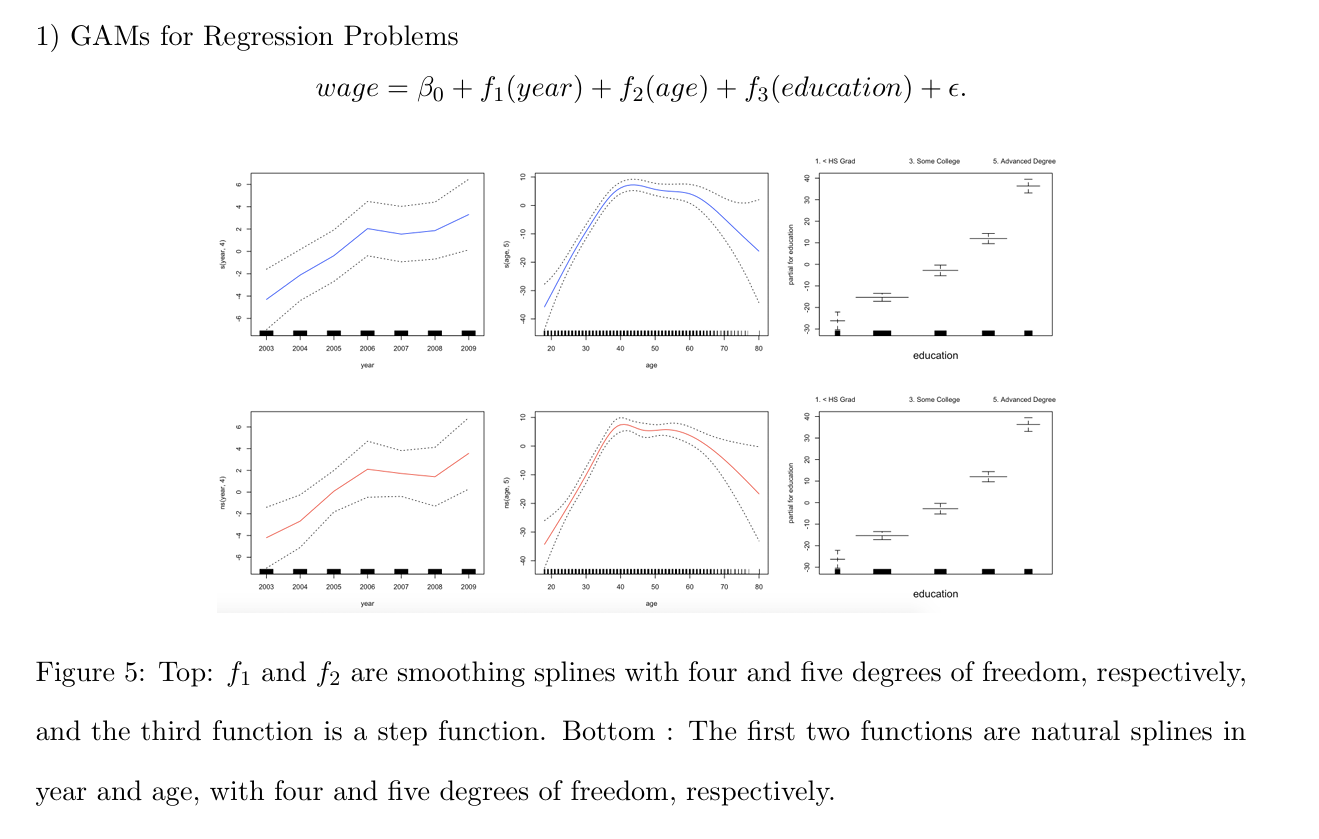
smoothing의 첫 번째 그래프를 보면 age와 edu가 고정되어있을 때의 그래프를 볼 수 있습니다.

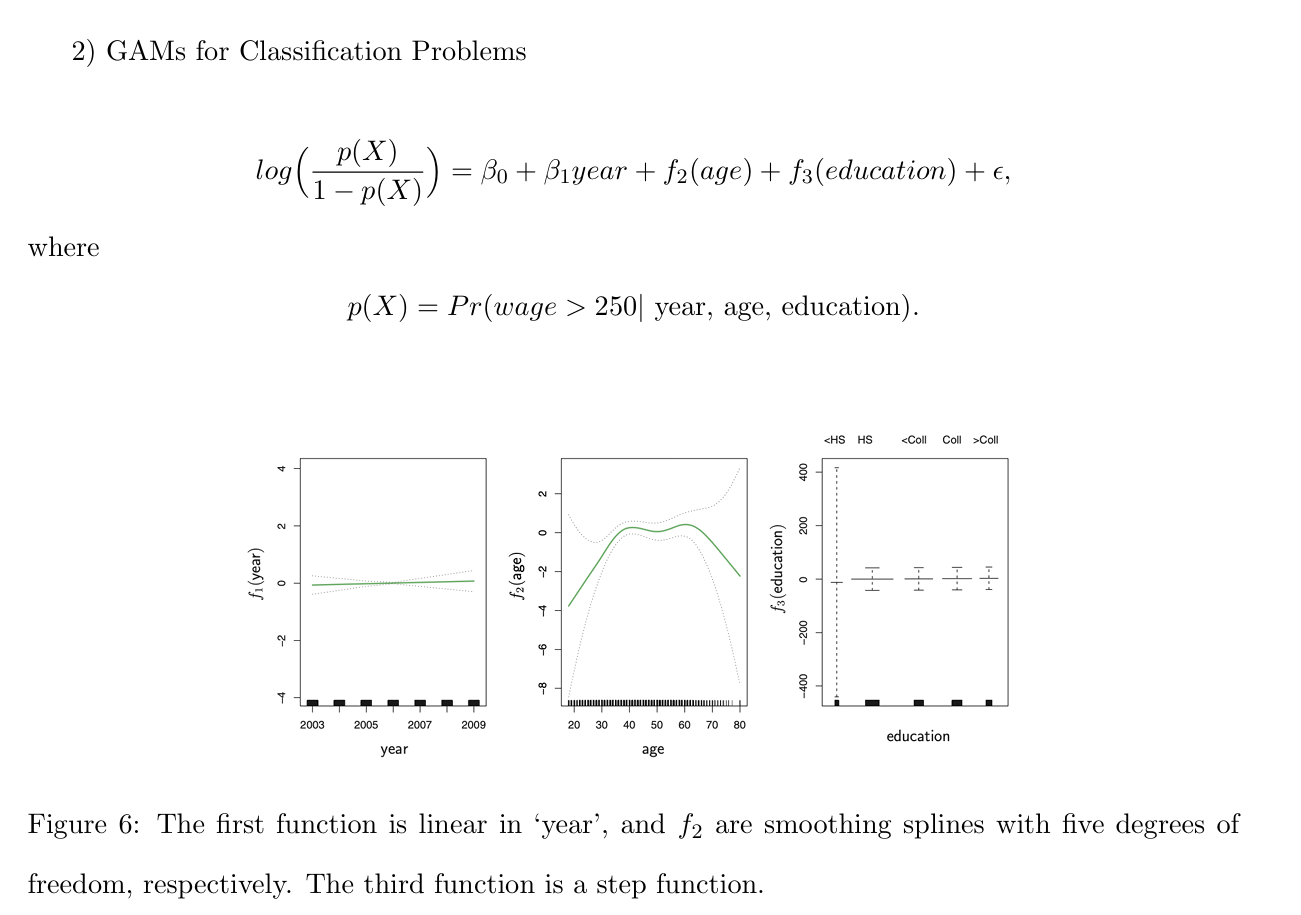
세 번째 그래프를 보면 CI(Confidence Interval)이 extreme한 것을 볼 수 있는데, 이는 250 초과하는 급여를 받은 데이터가 존재하지 않고 0만 존재했기 때문이라고 합니다. 위의 식을 보면, 250이 넘으면 1 그게 아니라면 (else) 0으로 coding 했기 때문에 이렇게 나타났다는 것을 알 수 있습니다.

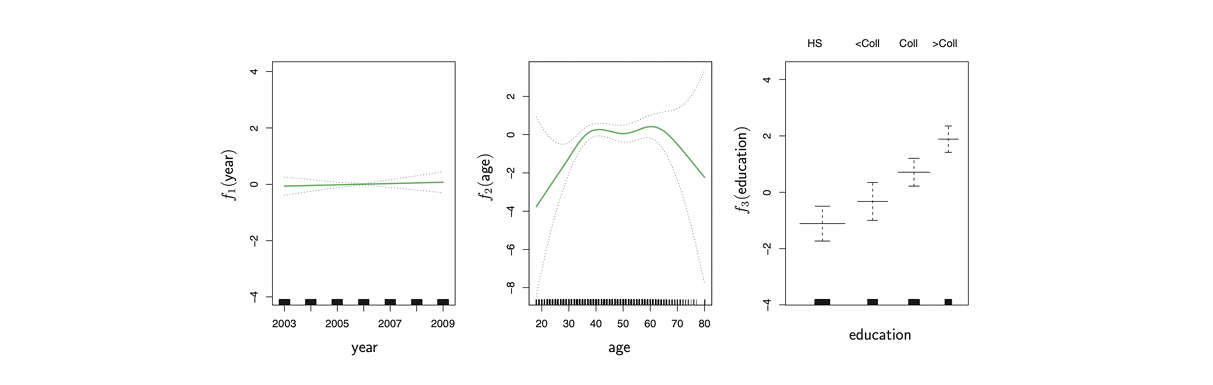
그래서 $<HS$ 라는 카테고리를 제거한 그래프입니다.