Linear Model Selection and Regularization

Subset Selection

Best Subset Selection
✔ 가능한 모든 모델을 고려하여 가장 좋은 모델을 선택
$1$. $M_0$이 아무 predictor를 포함하지 않는 null model이라고 할 때, 이 모델은 각 observation의 sample mean을 predict함
$2$. $k = 1,2, ... ,p$ :
$(a)$ $pCk$ model들을 정확히 $k$ predictors가 포함되도록 함
$(b)$ $pCk$ model 중 가장 좋은 모델을 고르고 $M_k$라 함.
➡ 가장 좋다는 것은 가장 작은 RSS를 가지고 있다는 것 or 가장 큰 $R^2$을 가지고 있다는 것
$3$. $M_0, ... , M_p$ 중 single best model을 하나 선택함.
➡ cross-validated prediction error, $C_p$, (AIC), BIC, adjusted $R^2$ 등을 사용

Forward Stepwise Selection
✔ 변수를 하나씩 추가해가면서 Model을 선택
$1$. $M_0$은 아무 predictor를 포함하지 않는 null model
$2$. $k = 0, ... ,p-1$ :
2-1) 모든 $p-k$ model들은 predictor를 하나씩 증가시킴
2-2) $p-k$ 모델들 중 $M_{k+1}$를 가장 좋은 것으로 고름
➡ 가장 좋다는 것은 가장 작은 RSS를 가지고 있다는 것 or 가장 큰 $R^2$을 가지고 있다는 것
$3$. $M_0, ... , M_p$ 중 single best model을 하나 선택함.
➡ cross-validated prediction error, $C_p$, (AIC), BIC, adjusted $R^2$ 등을 사용

Backward Stepwise Selection
✔ Full model로 시작하여 하나씩 변수를 제거하면서 최적의 Model을 선택
$1$. $M_p$는 모든 p개의 predictor를 포함하는 full model
$2$. $k = p, p-1, ... , 1$ :
2-1) $M_k$는 하나의 predictor를 제외한 모든 predictor를 포함하고 있는 모델 ➡ total : $k-1$
2-2) $k$ 모델들 중 $M_{k-1}$를 가장 좋은 것으로 고름
➡ 가장 좋다는 것은 가장 작은 RSS를 가지고 있다는 것 or 가장 큰 $R^2$을 가지고 있다는 것
$3$. $M_0, ... , M_p$ 중 single best model을 하나 선택함.
➡ cross-validated prediction error, $C_p$, (AIC), BIC, adjusted $R^2$ 등을 사용

• Mallow's $C_p = \frac{1}{2}(RSS + 2p\hat{\sigma}^2)$ 　　　p = #parameters

• $AIC = −2 log L + 2p$

• $BIC =\frac{1}{2}(RSS + log(n)p\hat{\sigma}^2)$

• Adjusted $R^2 = 1 − \frac{RSS/(n − p − 1)}{TSS/(n − 1)}$ 　　　TSS = Total Sum of Squares

Shrinkage

Ridge regression

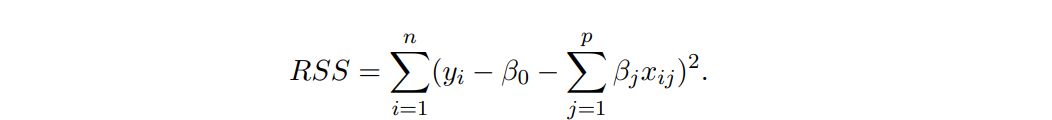
Ridge regression coefficients은 아래 식을 최소화하는 것이 목표임

➡ $\underset{\beta}{\arg\min}(RSS + \lambda\beta'\beta)$

$\lambda\beta'\beta$는 shrinkage penalty

• $\beta_j$가 0에 가까워질 수록 penalty term은 작아짐
• Ridge regression은 tuning parameter $\lambda$는 회귀 계수 추정에 두 항이 미치는 상대적인 영향을 조절하는 데 사용 (shrinkage 효과 조절)

➡ $\lambda$가 크면 RSS를 줄이는 것보다 $\beta'\beta$을 거의 0으로 줄여줘야 함
여기서 beta는 vector임

✔ $\lambda$가 0이라면 OLS와 동일 ➡ $\hat{\beta}^{ridge} = \hat{\beta}^{OLS}$
✔ $\lambda$가 점점 커짐에 따라 shrinkage 효과🔺 / Ridge Regression 계수들이 0에 가까워짐

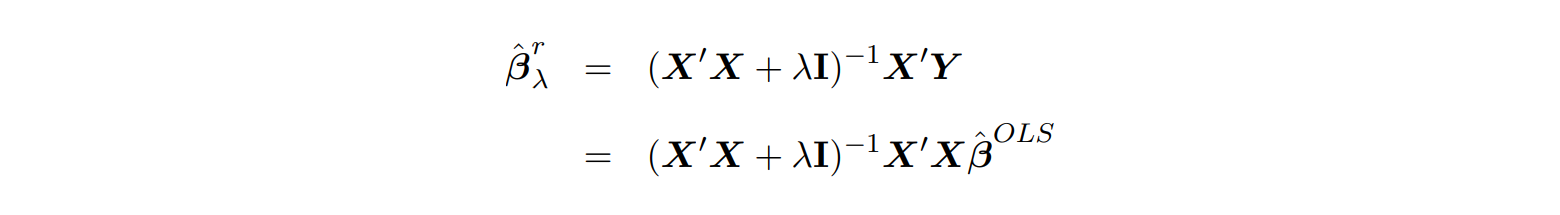
For special case of $X'X = I$ , $\hat{\beta}^r_\lambda = \frac{1}{1+\lambda}\hat{\beta}^{OLS}$

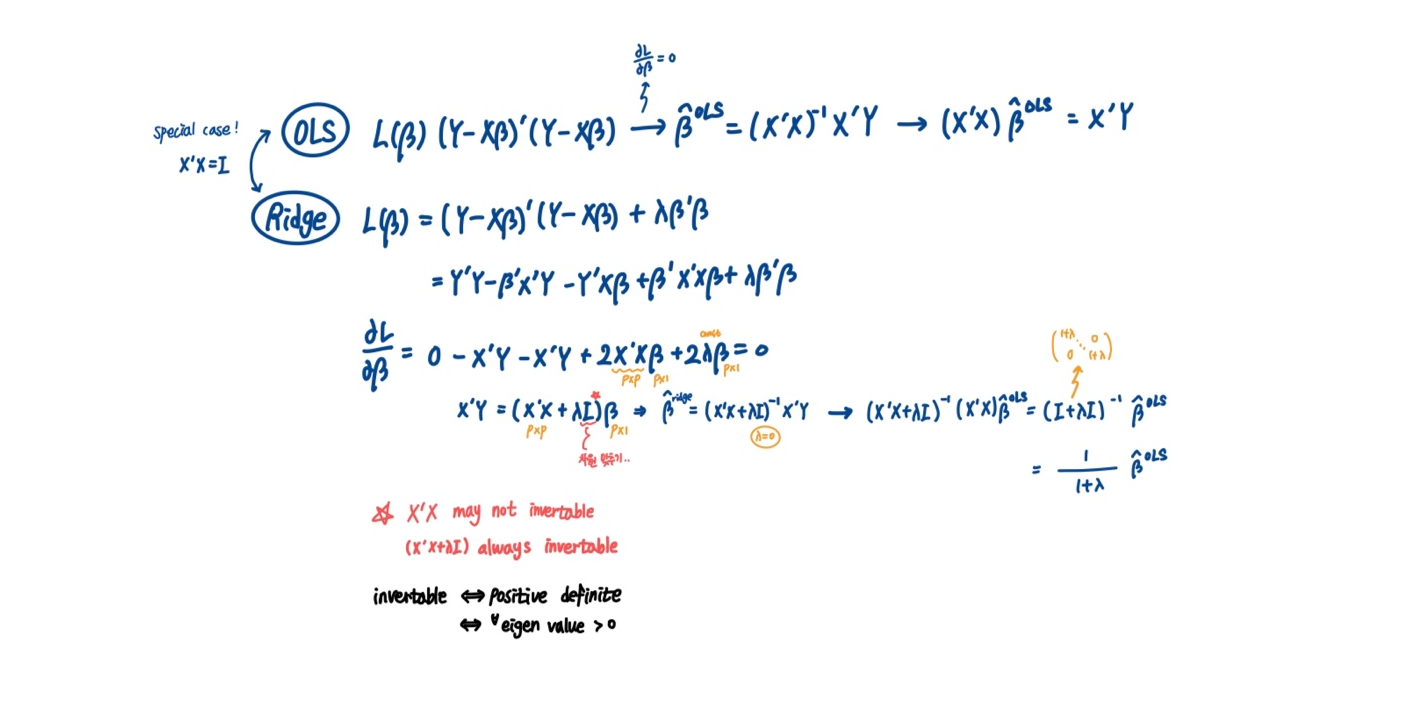
• ridge regression estimates는 predictor에 상수를 곱해주면 많이 변하기 때문에 (패널티 부분에 있는 계수 제곱의 합 때문) predictor들에 표준화를 거친 다음 ridge regression을 적용하는 것이 좋음

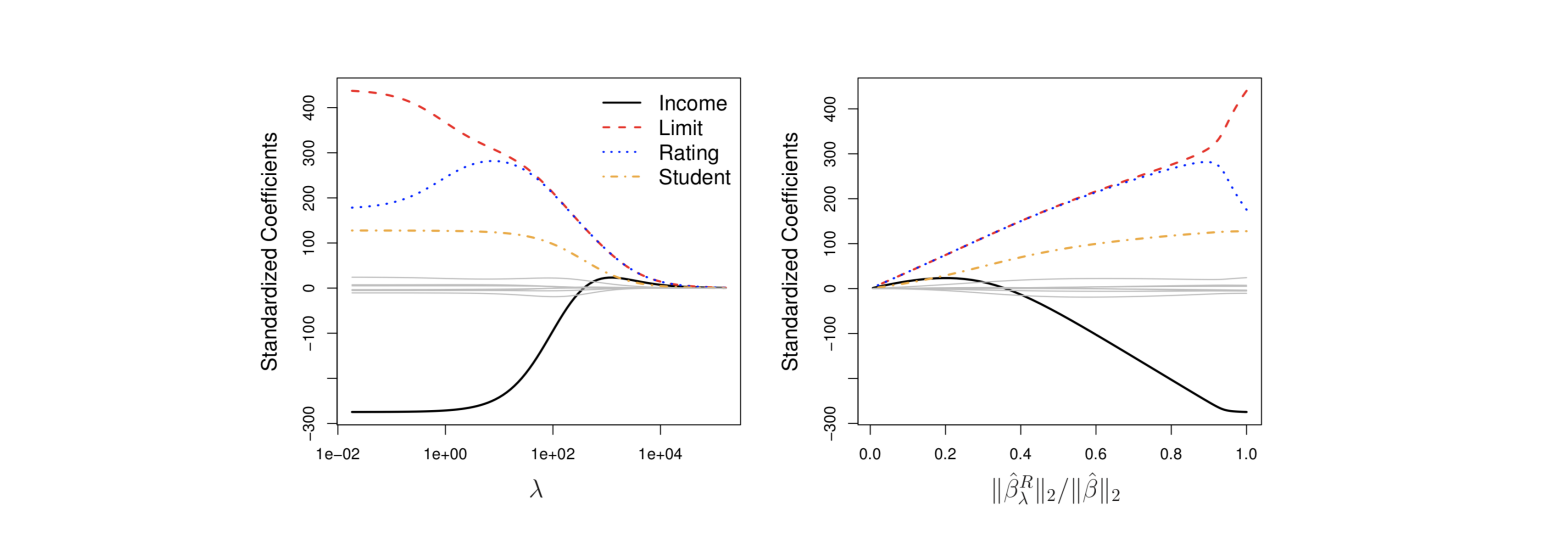
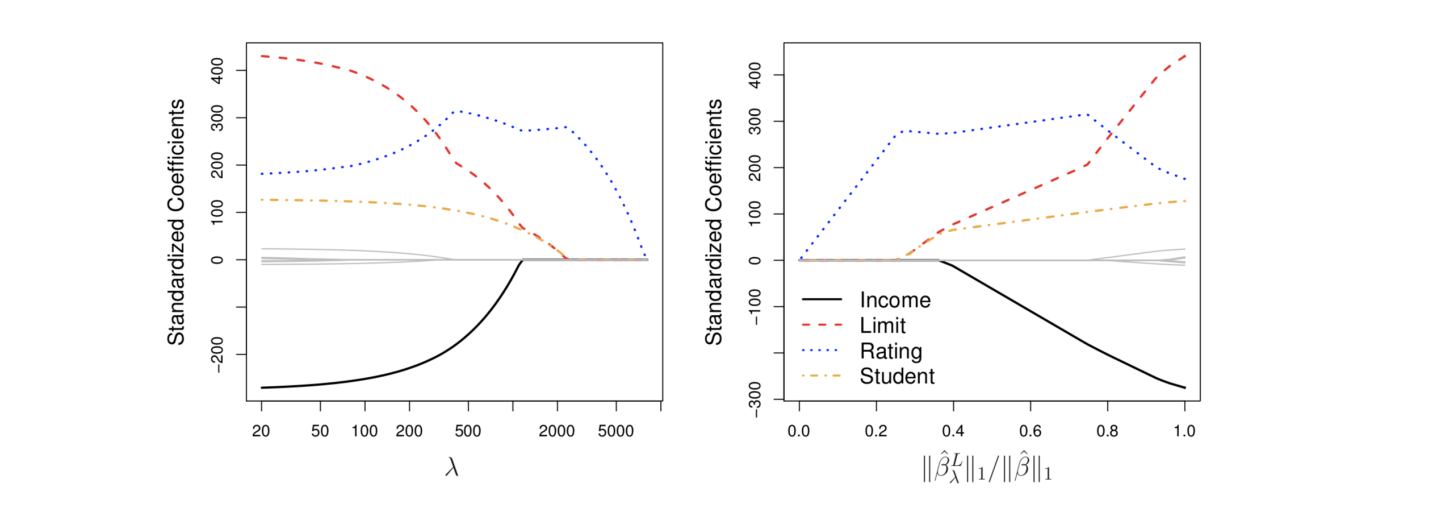
📈 effect of $\lambda$ value

• 왼쪽 그래프
  오른쪽으로 갈수록 $\lambda$이 점점 커짐
  오른쪽으로 갈수록 $\hat{\beta}^{ridge}$ 값 shrink (0에 가까워짐)

• 오른쪽 그래프
  왼쪽으로 갈수록 $\lambda$이 점점 커짐

📍Bias-Variance tradeoff

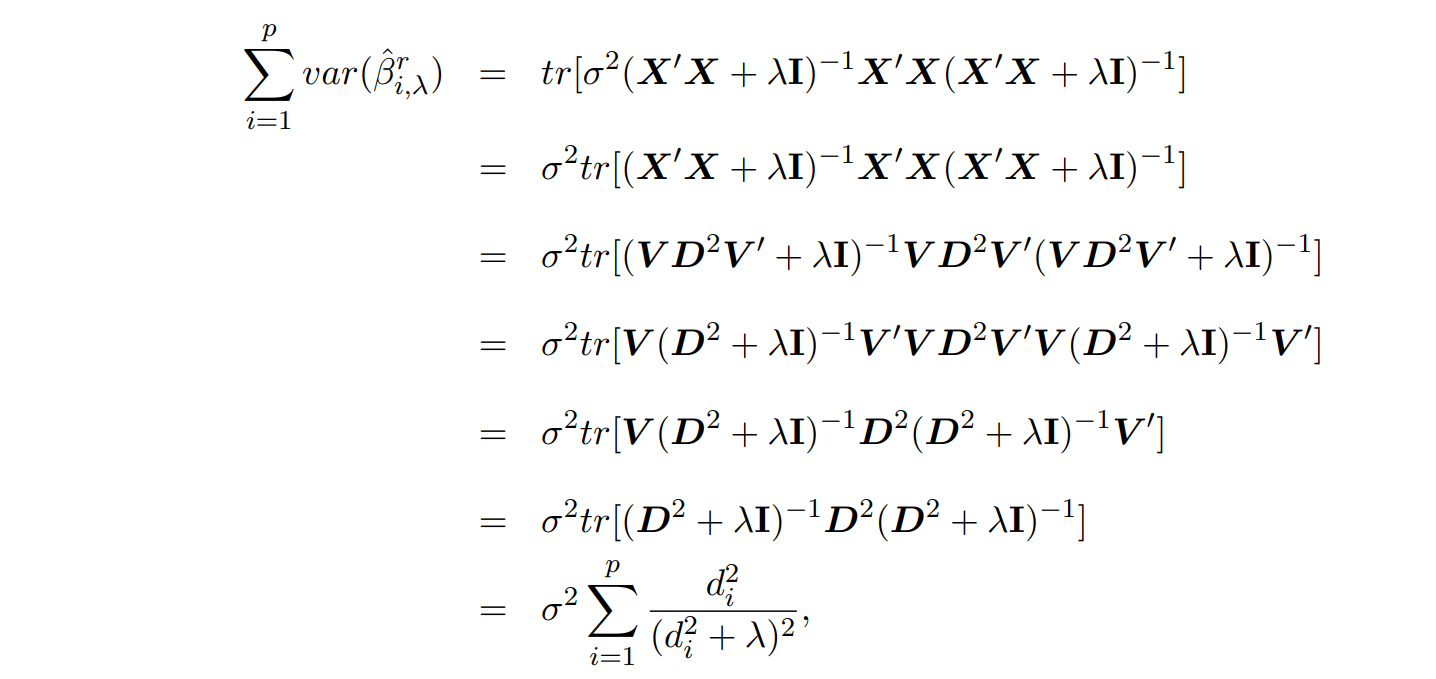
동일한 내용 필기본 ⬇

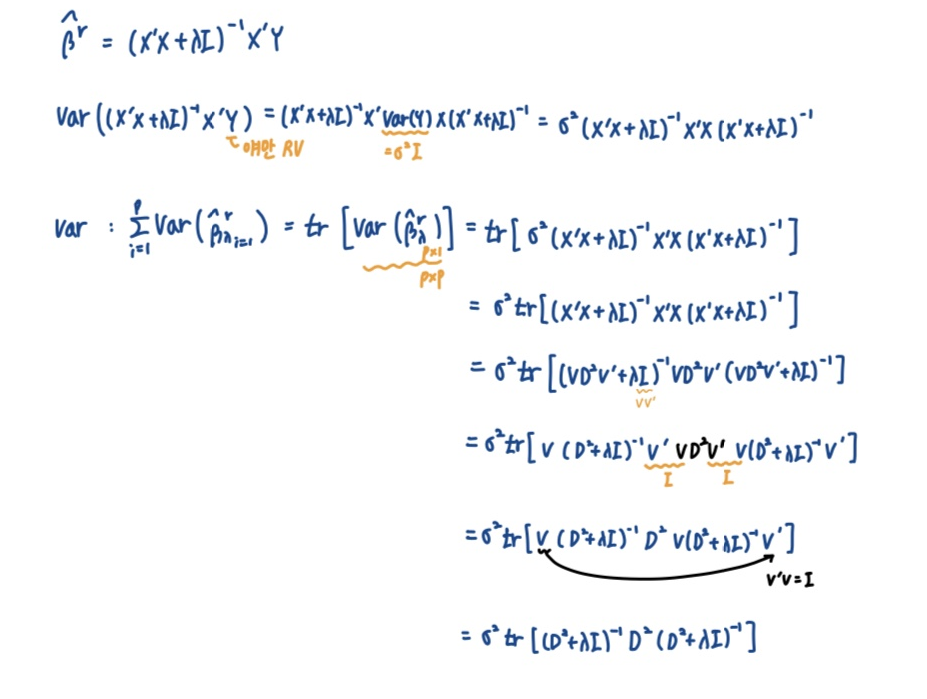
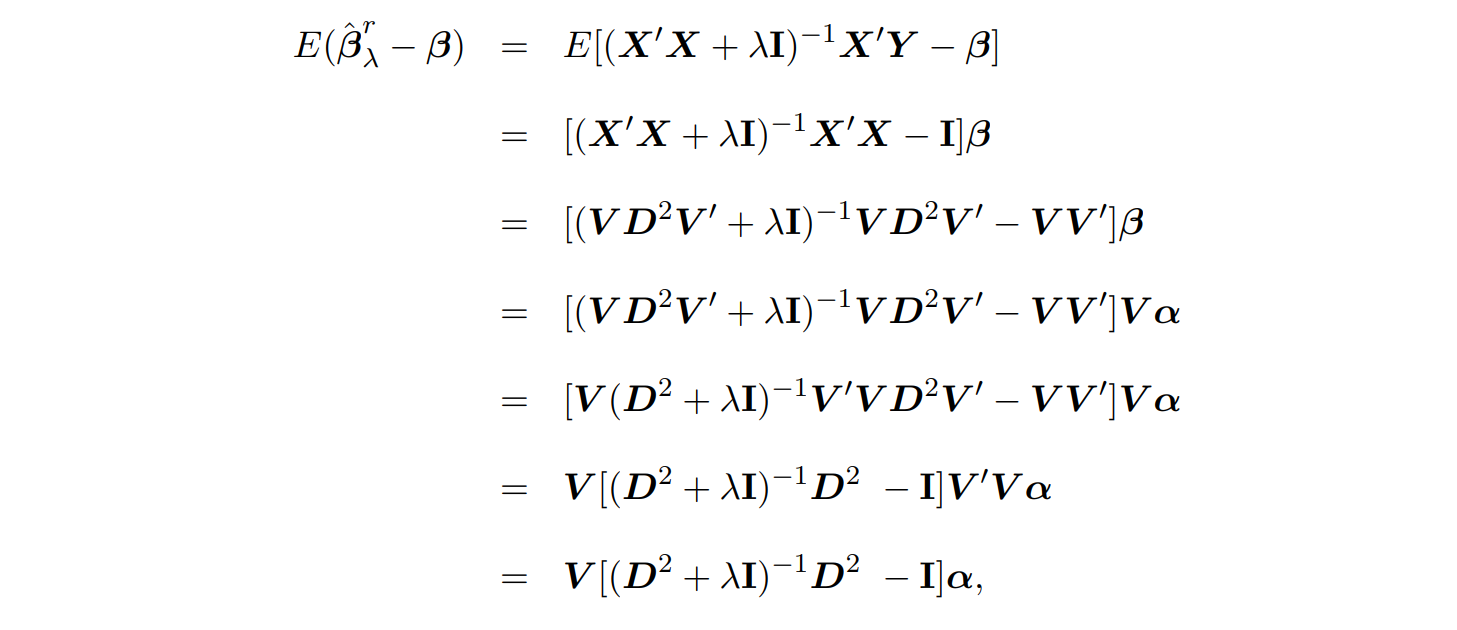
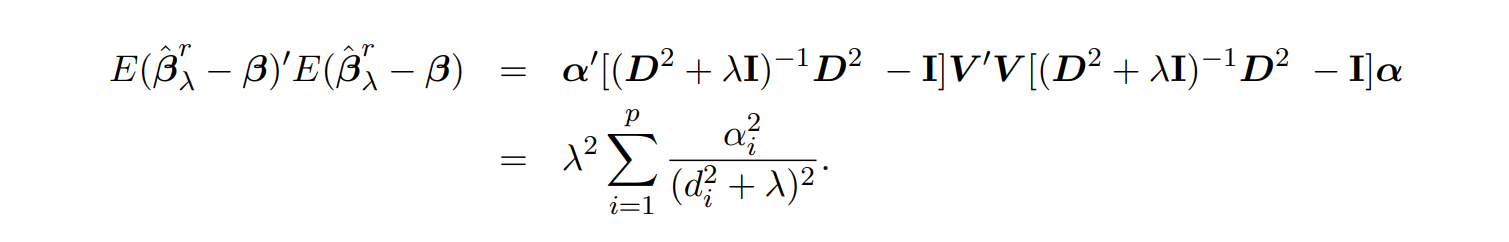
동일한 내용 필기본 ⬇

✔ 증명 과정에서의 SVD는 링크를 참고

The Lasso regression

📍 Lasso는 closed term이 존재하지 않음 ➡ penalty form이 미분 불가하기 떄문

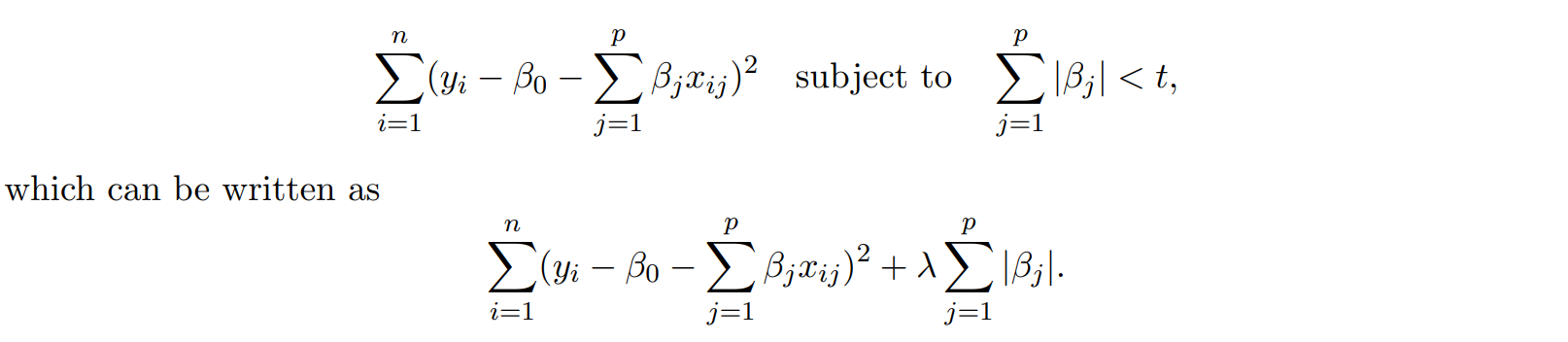
Ridge의 penalty term: $\beta_j^2$, Lasso의 penalty term: $|\beta_j|$
Lasso는 explit form을 만들 수 없지만, variable selection이 가능함 Ridge는 variable selection 불가능

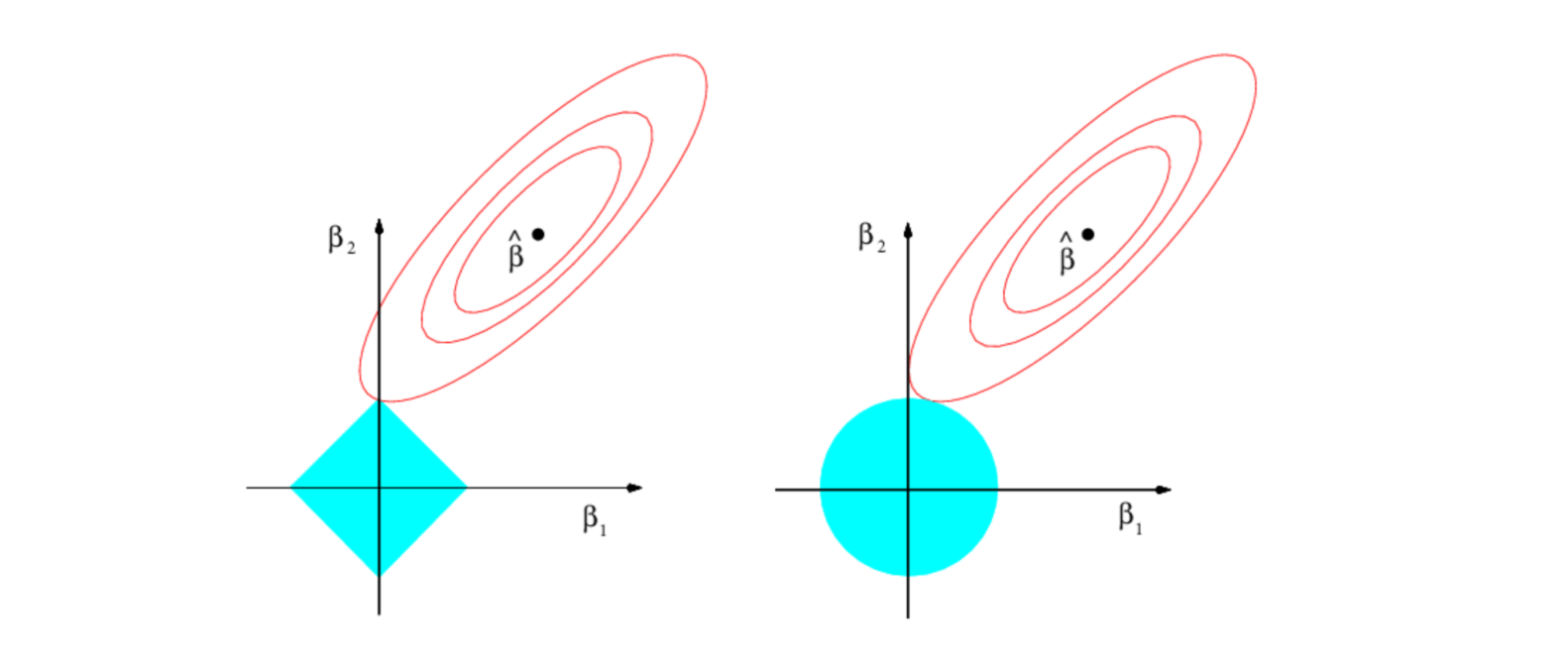
📈Lasso 왼쪽 그래프, L1 form

• variable selection 가능
• 타원에 있는 점 $\hat{\beta}$에서 Least squares estimator (제약조건 없는 경우 error 최소)
• 타원이 y축과 만나는 점에서 제약조건을 만족하며 error가 최소가 되고 이때 $\beta_1 = 0$이 되어 variable selection이 가능해짐
  제약조건 $|\beta_1| + |\beta_2| \leq t$

📈Ridge 오른쪽 그래프, L2 form

• variable selection 불가능
• 타원에 있는 점 $\hat{\beta}$에서 Least squares estimator (제약조건 없는 경우 error 최소)
• 타원이 원과 만나는 점에서 제약조건을 만족하며 error가 최소
• $\beta_1$, $\beta_2$ 둘다 0이 아니기 때문에 selection이 일어나지 않음
  제약조건 $\beta_1^2 + \beta_2^2 \leq t$

Lasso는 closed form이 없지만, $X'X=I$인 special case에 한해 closed form을 구할 수 있음 X가 모두 orthogonal

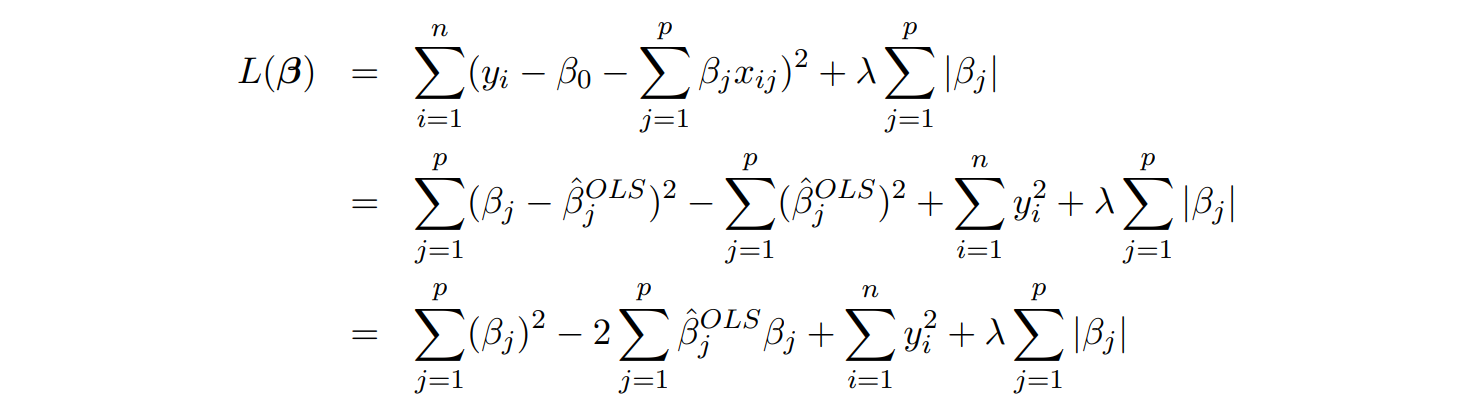
위의 식을 보면 $2\displaystyle\sum_{i=1}^{p} \hat{\beta}^{OLS}\ \beta_j^2$에서만 부호가 결정이 됨
만약 $\hat{\beta}^{OLS} > 0$ 이라면, $\beta_j$가 +일 때 $2\displaystyle\sum_{i=1}^{p} \hat{\beta}^{OLS}\ \beta_j^2$이 -가 되고,
$\beta_j$가 -일 때 $2\displaystyle\sum_{i=1}^{p} \hat{\beta}^{OLS}\ \beta_j^2$이 +가 됨.

$\hat{\beta}^{OLS} > 0$인 경우 ⬇

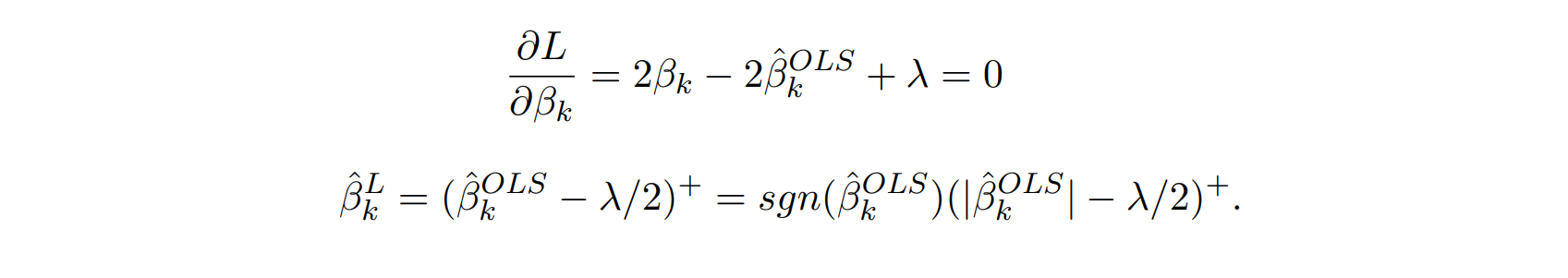
$sgn()^+$는 $\geq0$이면 괄호 안에 식을 그대로 사용하고 $<0$이면 괄호 안에 식이 0이 됨
➡ $\beta_j$가 작아지는 것이 goal이기 때문에 더 큰 값이 될 바에 0이 되는 것이 작은 값에 도달할 수 있어 sgn form을 사용함

sgn으로 표현된 마지막 form이 더 복잡해보일 수 있지만 $\hat{\beta}^{OLS} < 0$인 경우와 동일한 form을 가지기 때문에 일부러 이렇게 표현

$\hat{\beta}^{OLS} < 0$인 경우 ⬇

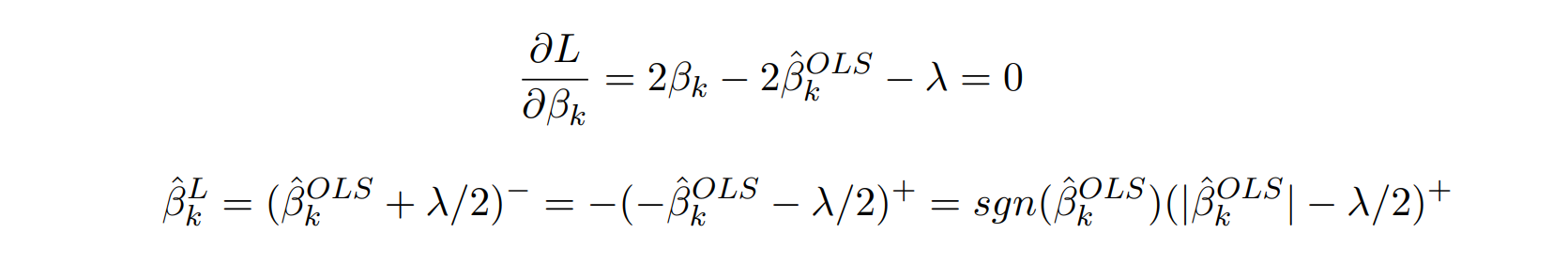
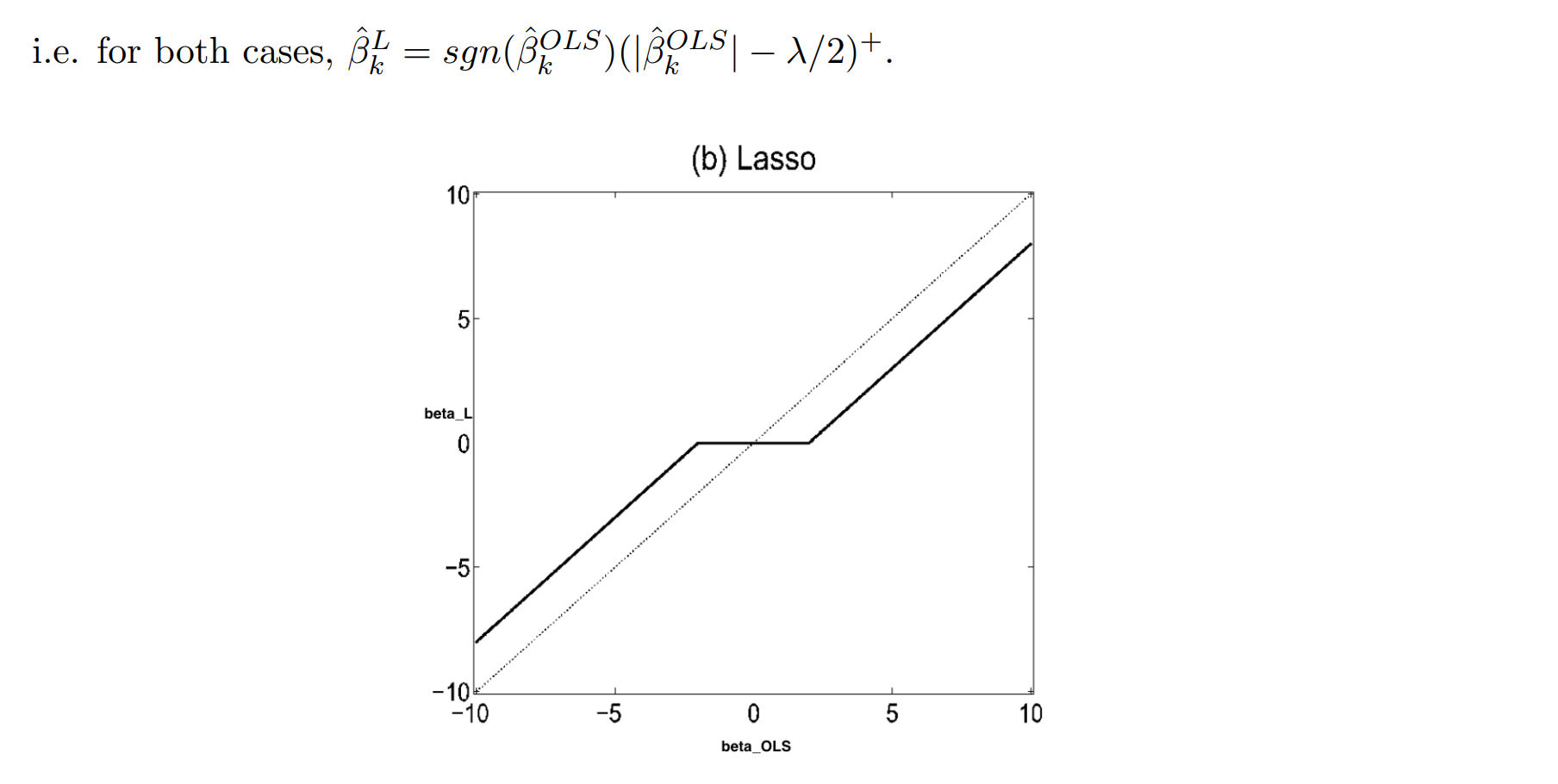
➡ 수평선이 되는 구간에서 $\beta_j = 0$이 돼서 variable selection 가능
➡ 흐릿하게 생긴 선이 ${\beta}_j^{Ridge}$, 진한 선이 ${\beta}_j^{Lasso}$

✔ Lasso는 Ridge와 달리 표준화할 필요 X
✔ $\lambda$ 가 증가할 떄 bias 증가 ↔ variance 감소 trade off

---

Reference - Introduction to Statistical Learning