정수론-유클리드 호제법

이론

📖 유클리드 호제법
두 수의 최대공약수를 구하는 알고리즘.

📍 최대공약수

#최대공약수
def gcd(a,b):
	while b!=0:
		r=a%b
		a=b
		b=r
	return a
    

📍 최소공배수

def gcd(a,b):
	while b!=0:
		r=a%b
		a=b
		b=r
	return a
    
# 먼저 gcd() 함수 구현 후, 
def lcm(a,b):
	return int(a*b/gcd(a,b))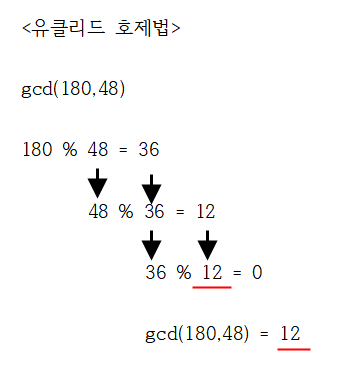

위의 유클리드 호제법을 이용하여 코드를 작성하면,

def gcd(a,b):
	if b==0:
		return a
    else:
    	return gcd(b,a%b)
        

문제풀이

📖 백준 1033 (🔗백준 1033 문제)

✏ 각 재료의 비율을 그래프로 구현.

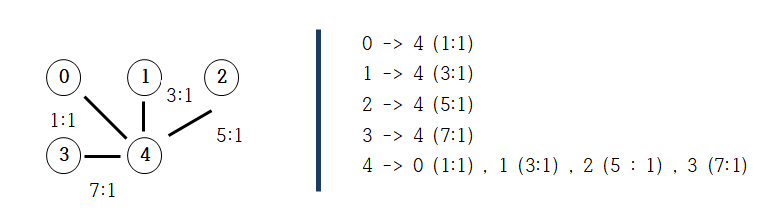
이를 바탕으로 인접리스트 작성 시, 튜플형태로 비율까지 포함시킨다.

for i in range(n-1):
	a,b,p,q=map(int,input().split())
	arr[a].append((b,p,q))
	arr[b].append((a,q,p))

✏ 데이터를 저장할 때마다, 비율과 관련된 수들의 최소공배수를 업데이트 시킨다.
위에서 작성한 반복문 안에 최소공배수를 업데이트시키는 코드를 추가하면, 아래와 같다.

#인접리스트 작성, lcm(최소공배수) 업데이트
for i in range(n-1):
	a,b,p,q=map(int,input().split())
	arr[a].append((b,p,q))
	arr[b].append((a,q,p))
	total_lcm*=lcm(p,q)

✏ 최대공약수, 최소공배수는 유클리드 호제법을 이용하여 따로 작성해놓는다.

✏ 임의의 시작점에서 DFS로 탐색을 수행하면서 각 노드의 값을 이전 노드의 값과의 비율 계산을 통해 계산하고 저장한다.

cf)
0을 임의의 점으로 선정할 때,
4 -> 0번 노드값 1/1 = 105
1 -> 4번 노드값 1/3 = 35
2 -> 4번 노드값 1/5 = 21
3 -> 4번 노드값 1/7 = 15

✏ 각 노드의 값을 모든 노드의 최대공약수로 나눈다.

📝 코드

# 유클리드 호제법, DFS

import sys
input=sys.stdin.readline

n=int(input())
arr=[[] for i in range(n)]
visit=[0]*n
total_lcm=1
ingredient=[0]*n

def gcd(a,b):
	while b!=0:
		r=a%b
		a=b
		b=r
	return a

def lcm(a,b):
	return int(a*b//gcd(a,b))

def dfs(a):
	visit[a]=True
	for i in arr[a]:
		next=i[0]
		if not visit[next]:
			#다음 노드 값=현재노드값*비율
			ingredient[next]=ingredient[a]*i[2]//i[1]
			#재귀
			dfs(next)

#인접리스트 작성, lcm(최소공배수) 업데이트
for i in range(n-1):
	a,b,p,q=map(int,input().split())
	arr[a].append((b,p,q))
	arr[b].append((a,q,p))
	total_lcm*=lcm(p,q)

#0번 노드에 최소공배수 저장, 0번부터 dfs탐색 시작.
ingredient[0]=total_lcm
dfs(0)
total_gcd=ingredient[0]

for i in range(1,n):
	total_gcd=gcd(total_gcd,ingredient[i])

for i in ingredient:
	print(i//total_gcd,end=" ")

◼ 참고사항

• Do it! 알고리즘 코딩테스트
• 백준