정수론-확장 유클리드 호제법

이론

📖 확장 유클리드 호제법
ax+by=c (a,b,c,x,y는 정수) 인 방정식의 해를 구하는 것.

📖 ax+by=c 인 방정식의 해 구하기.
위의 방정식은 c % gcd(a,b) == 0 인 경우에만 정수해를 가진다.
따라서, c는 gcd(a,b)의 배수이다.

이를 바탕으로, 180x+48y=12 일 때 이 식을 만족하는 정수 x,y값을 구해보면,
1) gcd(180,48)=12이므로 위 방정식은 정수해를 가진다.

2) 유클리드 호제법을 이용하여 몫,나머지를 구한다.

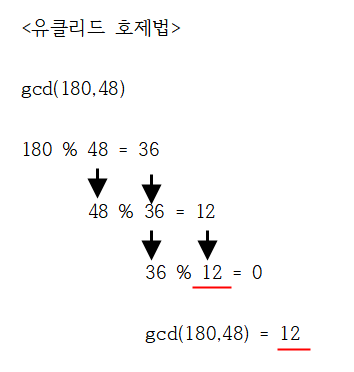
위 그림을 바탕으로,
나머지가 36 일 때, 몫은 3
나머지가 12 일 때, 몫은 1
나머지가 0 일 때, 몫은 3

3) 위에서 구한 몫과 나머지를 이용하여 x=y^, y=x^-y^*(몫) 을 계산한다. (역계산)
x^는 이전 x를 y^는 이전 y를 나타내고 처음 시작하는 값은 이전 x(x^)와 이전 y(y^)가 없으므로 1,0으로 지정한다.

나머지 0, 몫이 3일 때, x=0 y=1-0*(3)=1
나머지 12, 몫이 1일 때, x=1 y=0-1*(1)=-1
나머지 36, 몫이 3일 때, x=-1 y=1-(-1)*3=4

4) c/gcd(a,b)=K 라 가정하면, K=12/gcd(180,48)=1

5) 따라서, 180x+48y=12의 최초 방정식의 해는 x=-1, y=4 가 된다.

문제풀이

◼ 참고사항

• Do it! 알고리즘 코딩테스트
• 백준