CS229 | Lecture 2 - Linear Regression and Gradient Descent

HAIM BIN·2023년 7월 3일

cs229

Stanford CS229: Machine Learning

목록 보기

2/8

Outline

Linear regression
Batch/stochastic gradient descent
Normal equation

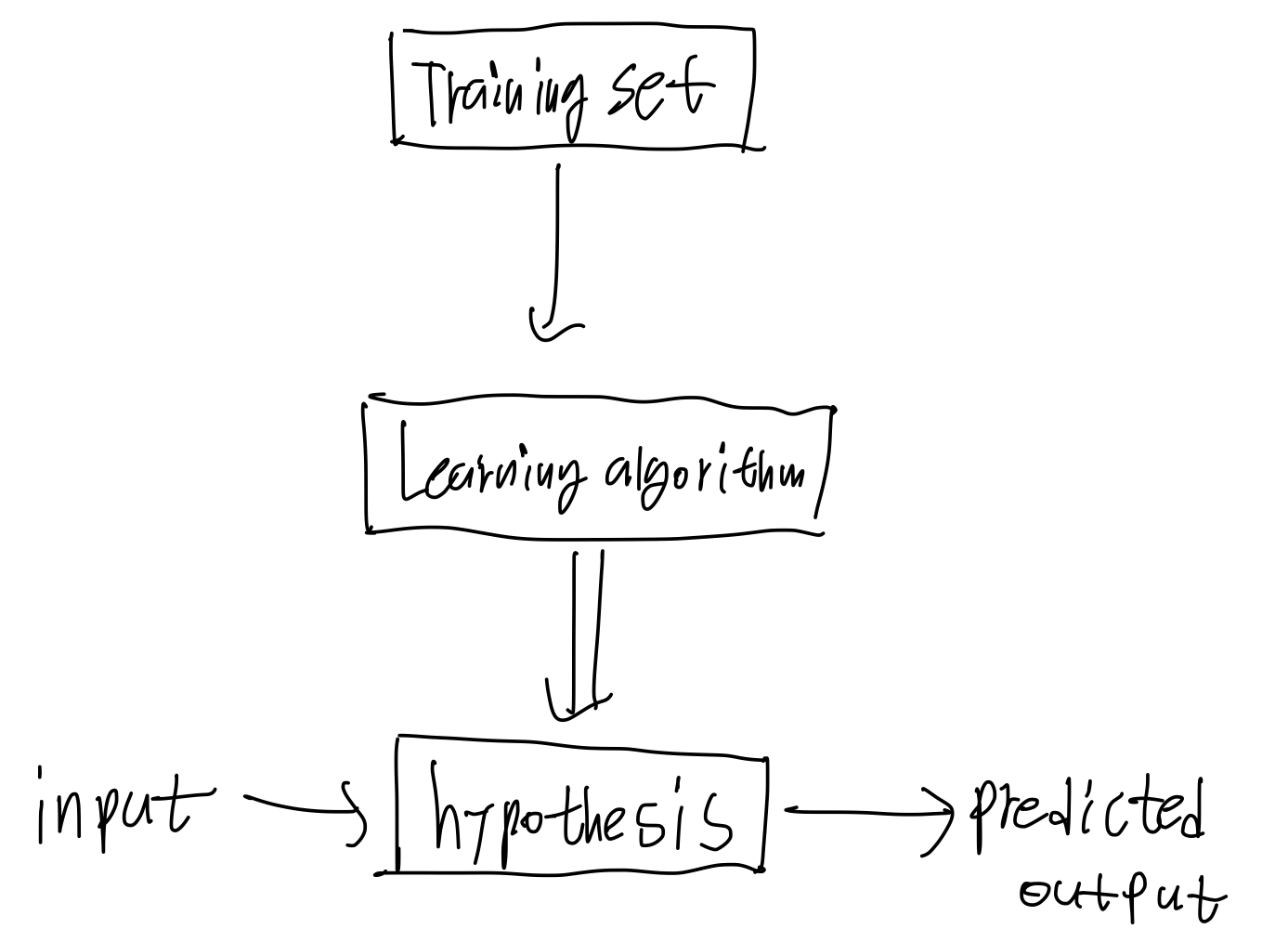
머신러닝중에서 지도학습은 어떻게 이루어지는가, 라고 누군가 물어본다면 다음과 같이 답할 수 있다.

Training Set을 어떤 알고리즘에 집어넣는다. 그리고 그 알고리즘은 하나의 함수를 출력한다(hypothesis, 가설이라고 부른다) 그리고 이 함수(가설)는input에 대해 output을 내놓는다.

Linear regression

linear regression은 한국어로 선형 회귀이다.
$h(x) = \theta_0 + \theta_1x$ 과 같은 식을 하나 만들었다고 해보자.
이러한 함수는 linear function 혹은 affine function이라고 부른다.
이 둘의 차이점에 대해서는 아래 링크를 참고하자.
linearfunction과 affine function의 차이점

결론부터 말하자면 affine function 이라고 하는게 더 정확하긴 하지만 머신러닝에서는 그렇게까지 용어의 엄밀함을 추구하지는 않는 듯 하다.

다시 돌아와 $h(x) = \theta_0 + \theta_1x$ 를 보면 이 함수는 하나의 feature만을 나타낼 수 있다. 즉 차원이 한 개 이다.

만약 $h(x) = \theta_0 + \theta_1x_1 + \theta_2x_2$ 이렇게 가정한다면 두개의 feature를 나타낼 수 있다. 즉 차원이 두 개이다.

일반적으로는 계산의 편의를 위해 $x_0$ 를 1로 설정해서 있는 것처럼 생각한다.

\sum _{j =0}^{2} {\theta_jx_j}

위와 같이 간단하게 쓸 수 있다.
위 식은 행렬로도 간단하게 표현할 수 있다.

\theta = \begin{bmatrix} \theta_0 \\ \theta_1\\ \theta_2 \end{bmatrix} , x = \begin{bmatrix} x_0\\ x_1\\ x_2\\ \end{bmatrix}

h(x) = \theta x

$\theta$ 는 parameter 라고 부른다.
$x$ 는 feature 라고 부른다.

learning algorithm 은 적절한 parameter : $\theta$ 를 찾는 과정이라고 말할 수 있다.

다음과 같이 용어를 더 정의할 수 있다.
# = number of
$m$ = #training examples
$x$ = inputs/feature
$y$ = output/target variables
$(x,y)$ = training example

$n$ = #feature
$n$ features => $n+1$ dimension

Gradient descent

경사하강법은 머신러닝에서 주로 가장 많이 쓰이는 최적화 알고리즘이다. 우리가 산 꼭대기에 있다고 가정해 본다면, 지면으로 내려가기 위해 현재 위치에서 가장 가파른 곳으로 내려가는 방법을 생각해볼 수 있다. 이처럼 경사하강법은 현재 위치에서 주위를 둘러보고, 가장 가파른 곳으로 이동하는 알고리즘이다.

경사하강법에서는 줄이고자 하는 목적함수를 잘 설정해야 한다. 일반적으로 linear regression 에서는 MSE (mean square error)를 사용한다. 실제 값과 가설로 나오는 값의 제곱을 오차를 최소화 하는 목적함수이다.
(왜 제곱을 사용하는가?에 대해 다음 포스트에서 다루겠다.)
여담으로 linear function 에서 MSE는 global optimal만을 가지고 있다. 왜냐하면 MSE는 convex 하기 때문이다.

우리의 목적을 다음과 같이 쓸 수 있다.

Choose $\theta$ such that $h(x) \approx y$ for training example

$h_\theta(x) = h(x)$
$J(\theta) = \frac{1}{2}\sum_{i=1}^{n}{(h_\theta(x^i)-y^i)^2}$
$\underset \theta {minimize} \ J(\theta)$

Gradient descent =>
Start with some $\theta$ (ex : 0 vector)
keep changing $\theta$ to reduce $J(\theta)$

Gradient descent는 다음과 같이 수식으로 적을 수 있다.

\theta_j := \theta_j - \alpha \frac{\partial}{\partial\theta_j}J(\theta)

여기서 $:=$ 의 의미는 assign 한다는 뜻이다.

목적함수를 미분하게 되면 깔끔하게 정리가 된다.

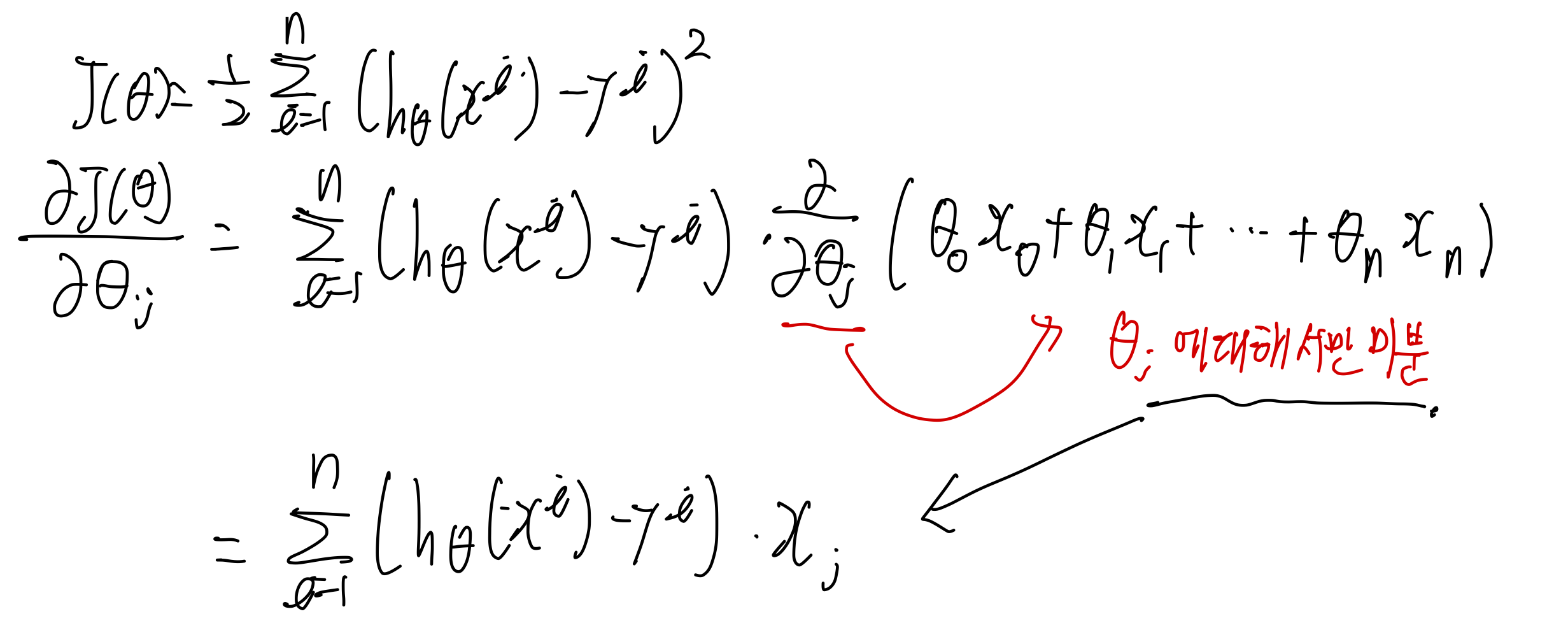
위 예시는 하나의 traing sample 에 대해서 미분한 것이다.
각각의 training sample의 미분의 합은 training sample을 전체 합한 것의 미분과 같다.

Batch gradient descent는 모든 샘플을 통과시켜 $\theta$ 의 변화량의 평균을 구한 뒤에 update를 수행하는 방법이다. 이 방법은 안정적으로 수렴하게 해주지만, 실제 세계에서 수억개의 데이터를 사용할 때는 expensive 하고 시간이 너무 오래걸려서 잘 사용하지 않는다.

Batch gradient descent는 모든 샘플을 통과시켜 gradient를 구한 후에 그것들의 합 또는 평균으로 parameter를 update한다.

MSE의 실제 이름은 "mean" square error이지만 합인지 평균인지는 그렇게 중요하지 않다. 중요한 것은 전체 sample이 parameter를 update 할 때 사용된다는 것이다.

Stochastic gradient descent는 하나의 샘플을 통과시켜 $\theta$ 의 변화량을 구하고 update를 수행하는 방법이다. 확률적으로 local optimal 에 가까이 가도록 해주지만, 확률적이기 때문에 수렴하지는 않는다. 그러나 수렴하지 않더라도 local optimal 근처로 보내주기 때문에 쓸만한 결과를 가져온다.

Stochastic gradient descent는 하나의 샘플을 통과시켜 gradient를 구한 후 parameter를 update 한다.

실제상황에서는 4,8,16,32 개 등의 sample을 통과시킨 후에 평균을 구하고 update 하는 minibatch를 많이 사용한다.

Normal Equation

affine function(이게 더 간지나니까 이렇게 부르자)의 경우에는 한 방에 global optimal 에 도달하도록 해주는 일반 방정식이 존재한다. 고등학교때 극솟값이나 극대값을 찾기 위해서는 도함수가 0이되는 지점을 찾으면 된다는 것을 배웠을 것이다. affine function에서도 이와 같은 과정을 이용해 한 번에 global optimal 을 찾을 수 있다.

즉 우리의 목적함수 $J(\theta) = \frac{1}{2}\sum_{i=1}^{n}{(h_\theta(x^i)-y^i)^2}$ 이므로 여기서 바로 미분을 때려버리고 0이 되는 parameter를 찾으면 된다. 우리가 이렇게 해도 되는 이유는 목적함수가 convex 하기 때문이고 극솟값이 하나밖에 존재하지 않기 때문이다.