조금 전 강의를 위해 알아둬야 할 중요한 선형대수 지식을 정리해보겠다.
https://cs229.stanford.edu/ 이곳에 있는 강의 노트를 참고했다.
먼저 모든 벡터는 열벡터로 가정한다.

벡터곱의 표현

$A \times B$를 4가지 방식으로 표현할 수 있다. $A \in R^{}$
1.A의 행벡터와 B의 열벡터의 내적
2.A의 열벡터와 B의 행백터의 외적
3.A와 B의 열벡터의 곱표현
4.A의 행벡터와 B의 열벡터의 곱표현

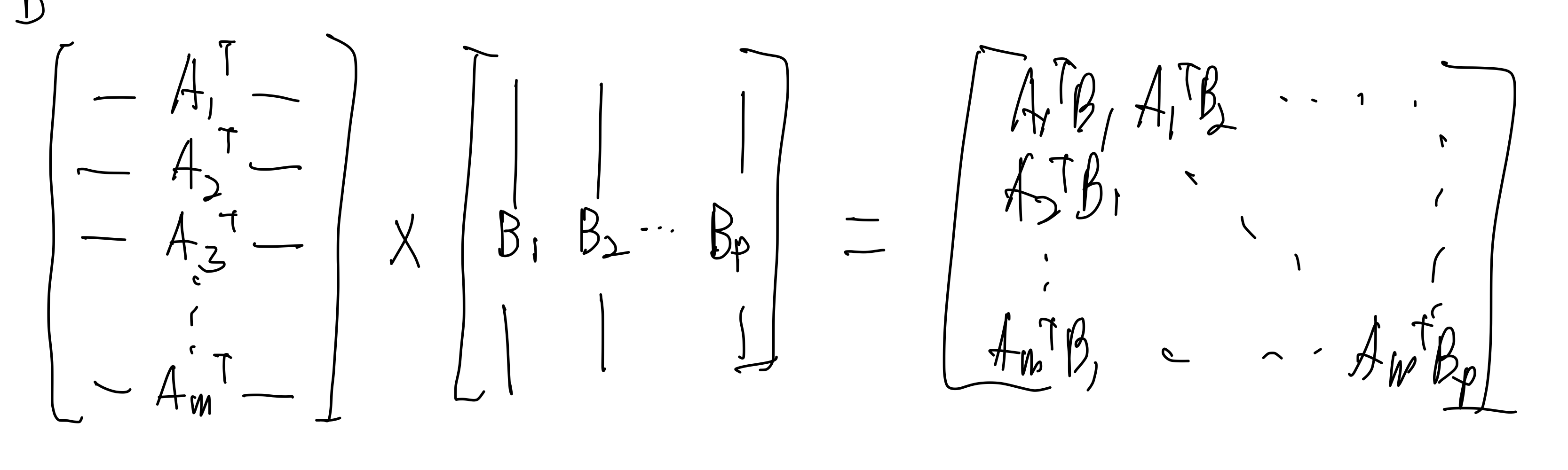
A의 행벡터와 B의 열벡터를을 차례대로 내적해서 표현하는 가장 일반적인 형태
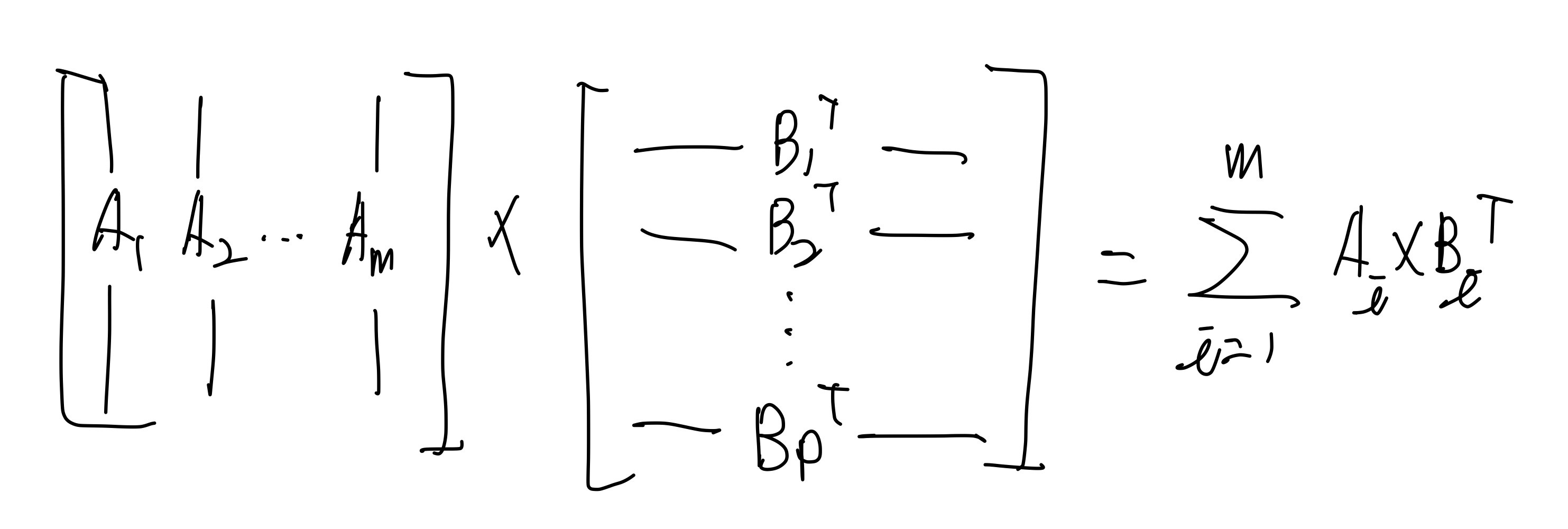A의 열벡터와 B의 행벡터를 차례대로 외적해서 표현하는 형태
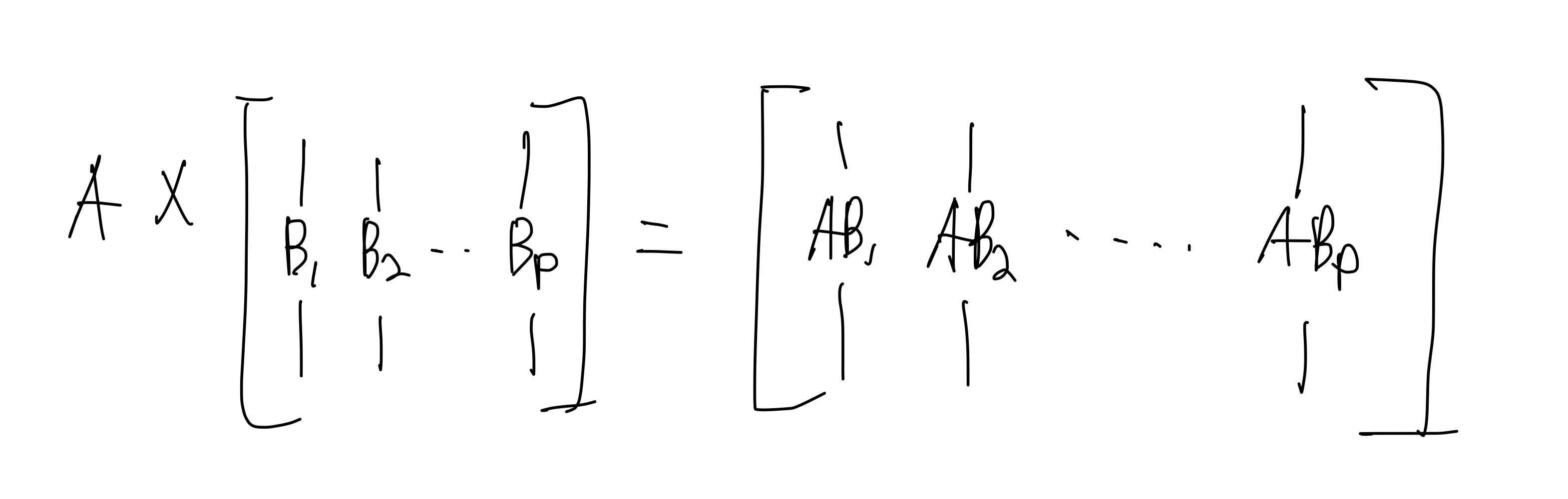A와 B의 열벡터를 곱하는 형태
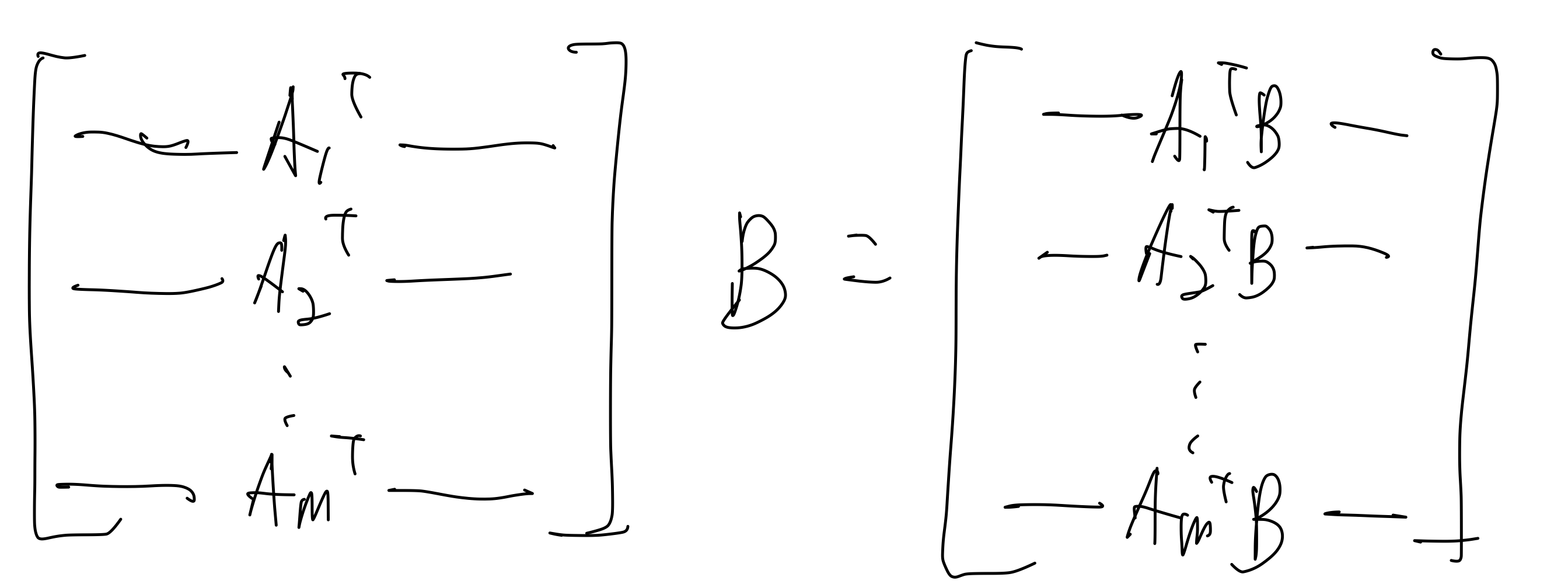A의 행벡터와 B를 곱하는 형태

A와 B의 행벡터를 곱하는 형태를 다루지 않는 이유는 차원이 맞지 않기 때문이다.

행렬의 결합법칙

$A \in R^{m\times n}$, $B \in R^{n\times p}$, $C \in R^{p\times q}$
라고 가정했을 때
$AB \in R^{m\times p}$, $(AB)C \in R^{m\times q}$ 이다.
그리고 또
$BC \in R^{n\times q}$, $A(BC )\in R^{m\times q}$ 이다.

어떤 행렬곱을 먼저 계산하더라도 차원이 같다.

다음으로 행렬곱을 수열의 합 형태로 나타내보겠다.

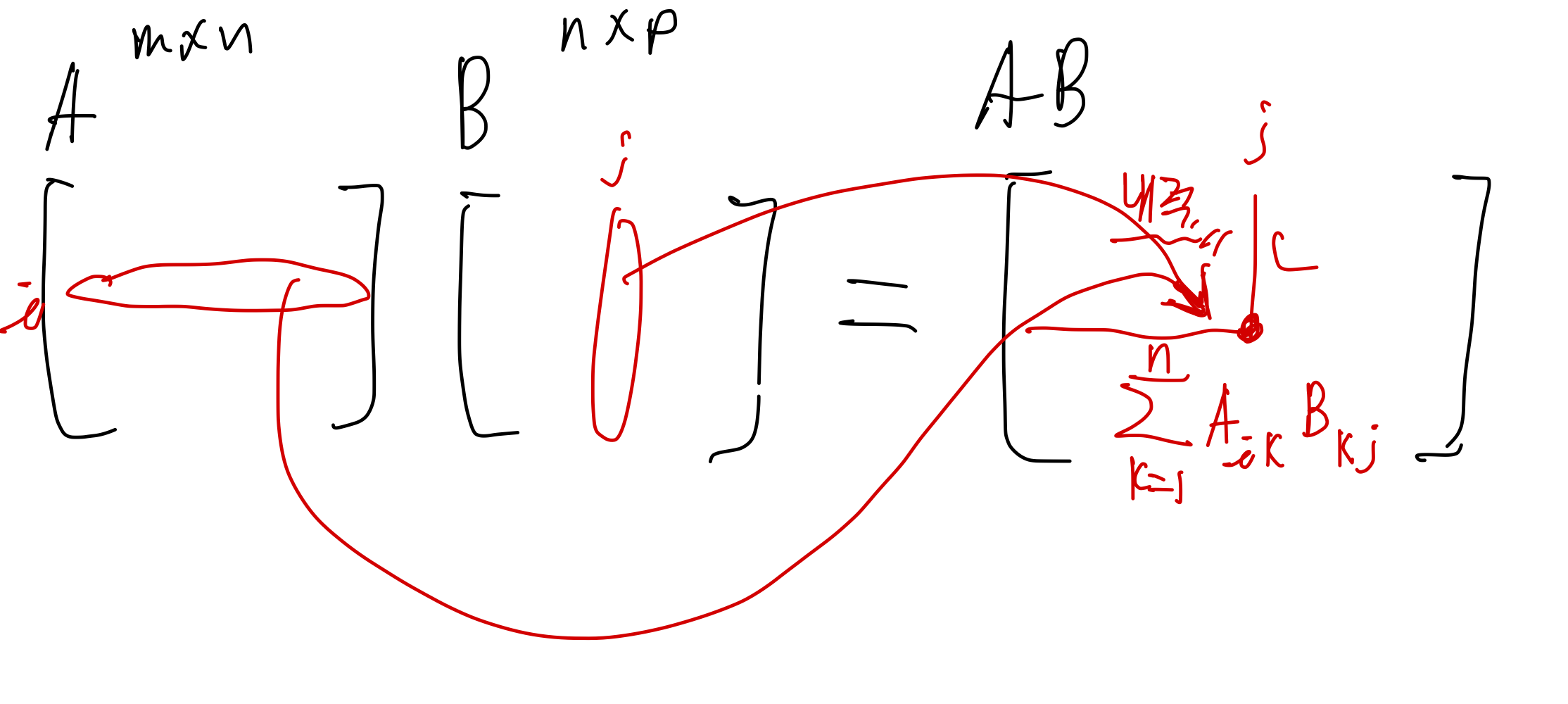
행렬곱을 수열의 합 형태로 나타내는 예시를 보이겠다.
$(AB)_{ij} = \sum_{k=1}^{n}A_{in}B_{nj}$ 다음과 같이 쓸 수 있다.
이를 소급해서 적용하면 $(AB)C = A(BC)$ 임을 알 수 있다.

$((AB)C)_{ij} = \sum_{k=1}^{p}(AB)_{ip}B_{pj} \\= \sum_{k=1}^{p}(\sum_{l=1}^{q}A_{il}B_{lk})C_{kj} \\= \sum_{l=1}^{q}\sum_{k=1}^{p}A_{il}B_{lk}C_{kj} \\= \sum_{l=1}^{q}\sum_{k=1}^{p}A_{il}(B_{lk}C_{kj}) \\ = \sum_{l=1}^{q}A_{il}(BC)_{lj} \\ = (A(BC))_{ij}$

이러한 규칙은 선형대수의 다양한 성질을 증명할 때 쓰이므로 알아두는 것이 좋다.

Quadratic form

$X^\intercal A X$ 를 quadratic form 이라고 부른다.
여기서 $X$ 는 $1\times n$크기의 열벡터이다. 그리고 $A$는 당연하지만 $n \times n$ 크기의 정사각형 벡터이다. 그리고 이 식의 결과값으로는 scalar가 나온다. 일반적으로 $A$ 를 symmetric 하다고 가정한다. 이는 문제를 단순화 하기 위함이다.
symmetric 하다는 것은 전치를 시키더라도 자기 자신이라는 것을 의미한다.

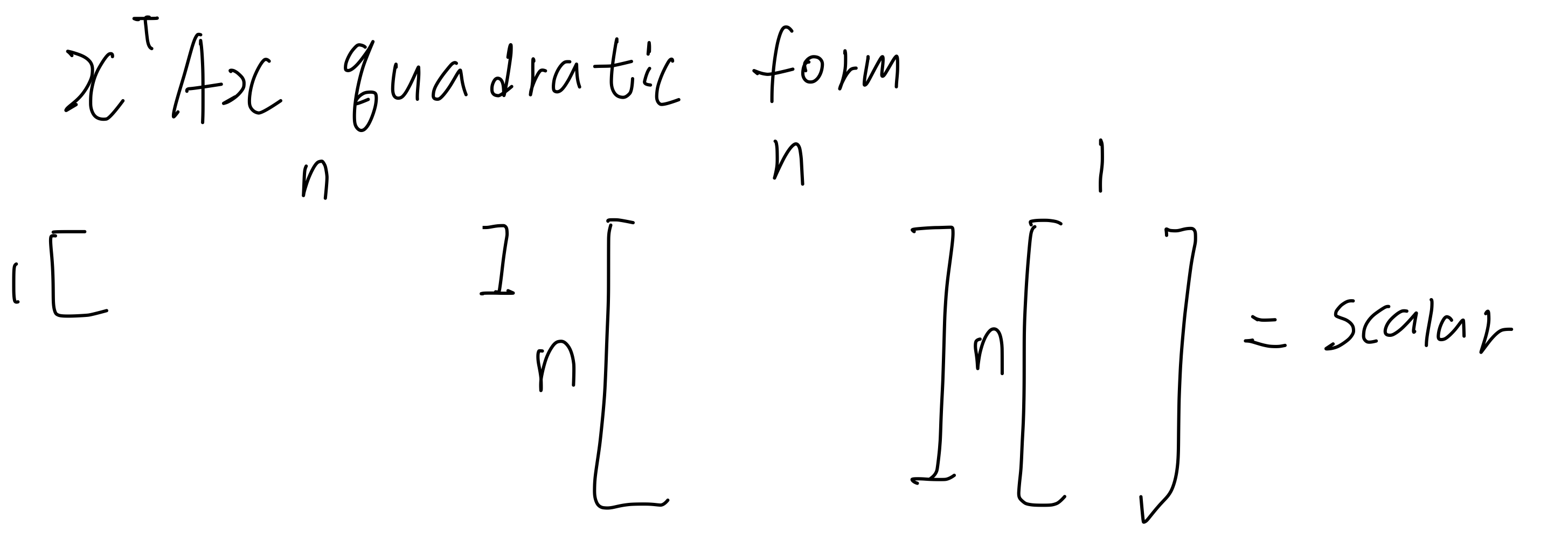
이 식을 수열의 합으로 풀어서 쓰면 다음과 같다.

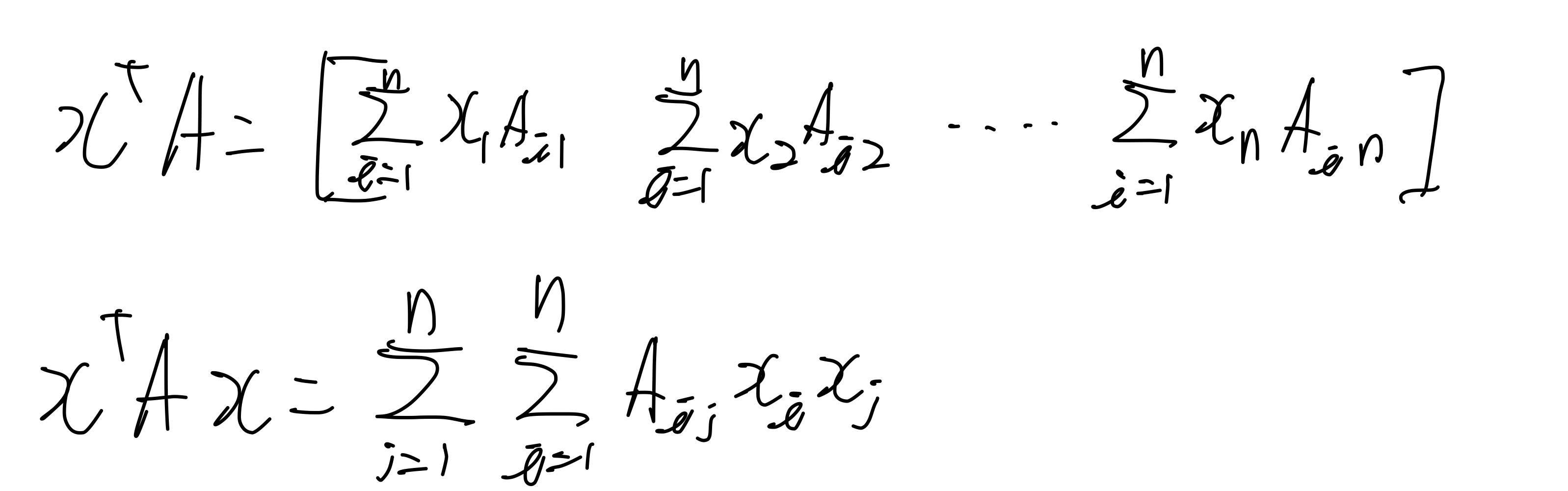
A가 symmetric 하므로 다음과 같은 성질을 가진다.

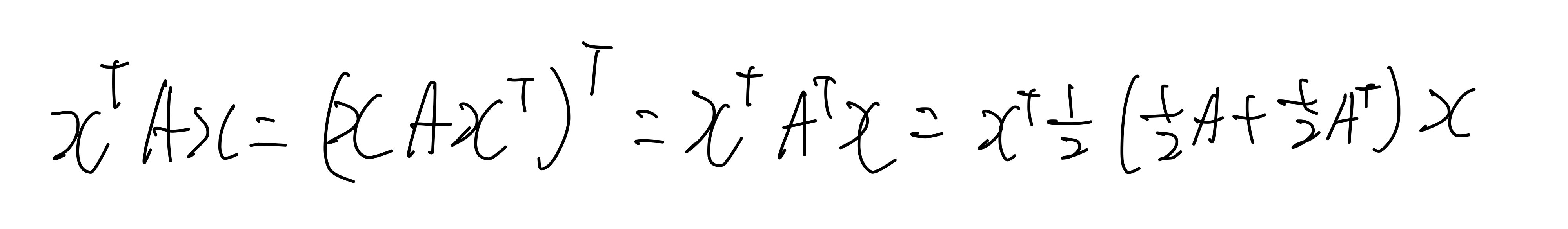
이제 quadratic form 을 미분할 것인데, 그전에 일차방정식 형태의 행렬을 미분해보자.

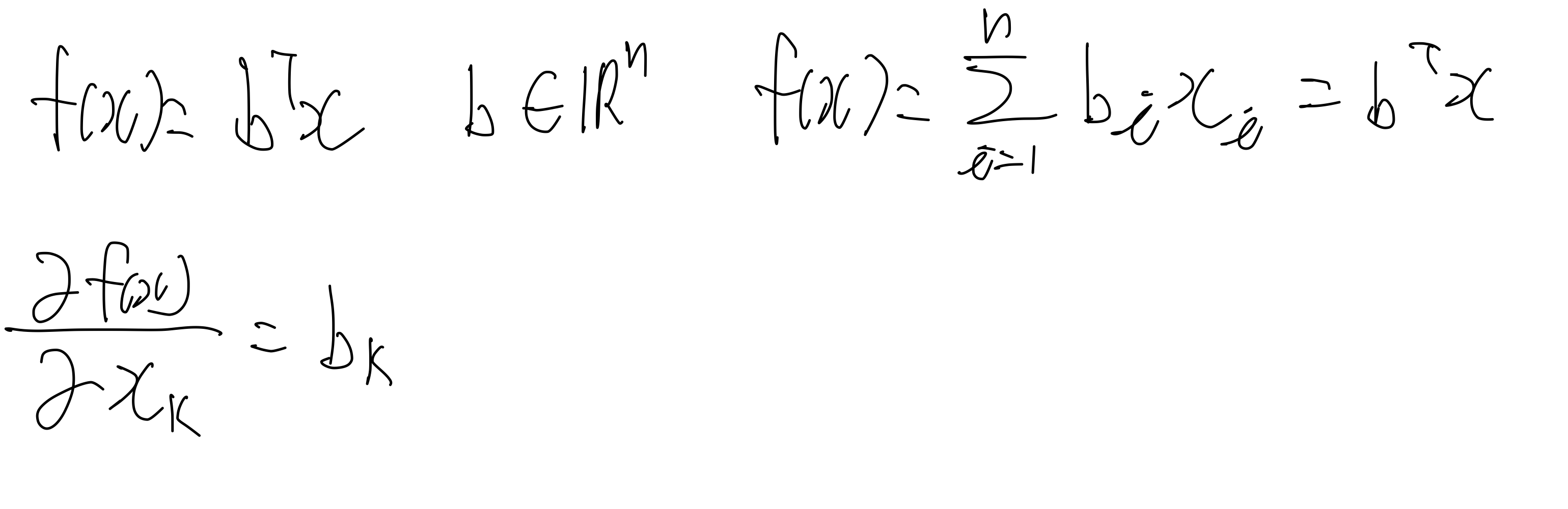
위와 같이 미분이 된다. 위에서는 $x_k$ 에 대한 미분만을 나타낸 것이고, 전체 미분은 또 다시 행렬 형태로 나타낼 수 있다. 이것을 야코비안이라고 부른다.

이차방정식도 이와 비슷하게 미분을 수행할 수 있다. 그러나 조금 더 까다롭다.
위에서 유도한 식들을 사용한다.

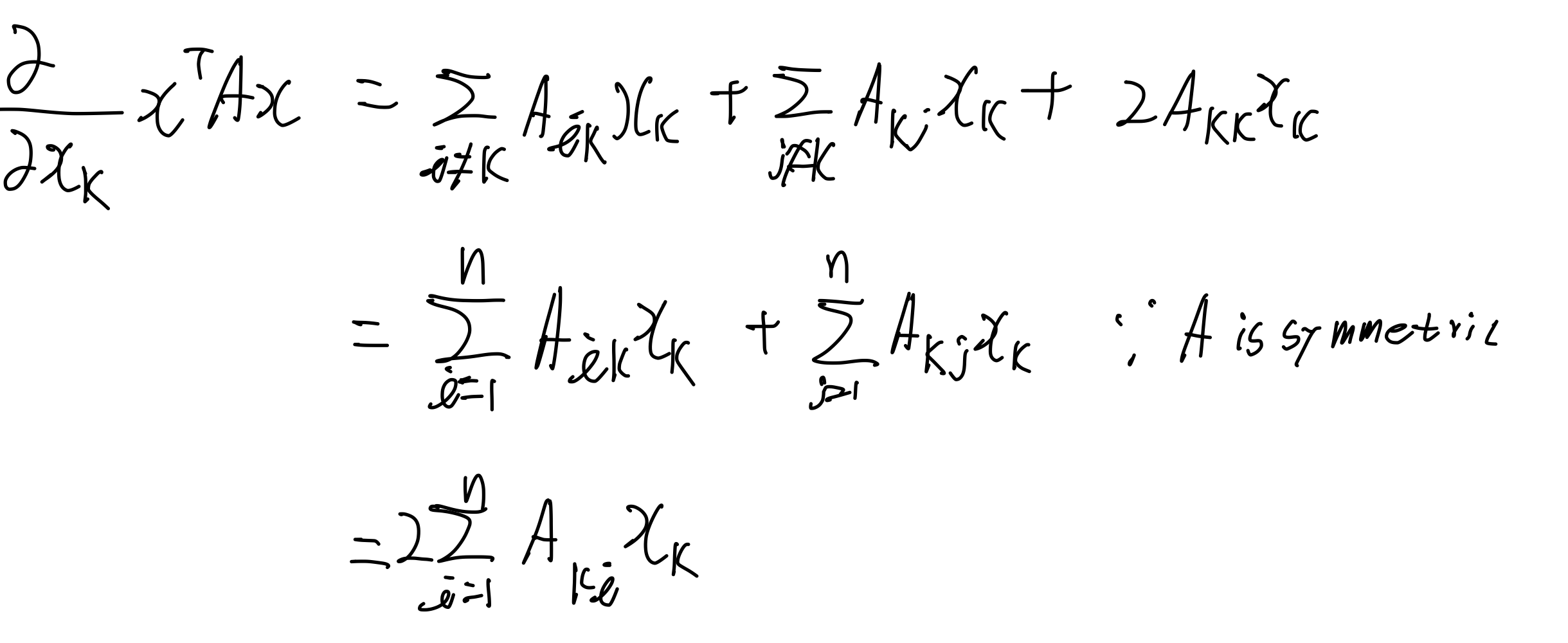
위는 하나의 $x_k$ 에 대한 미분이다.

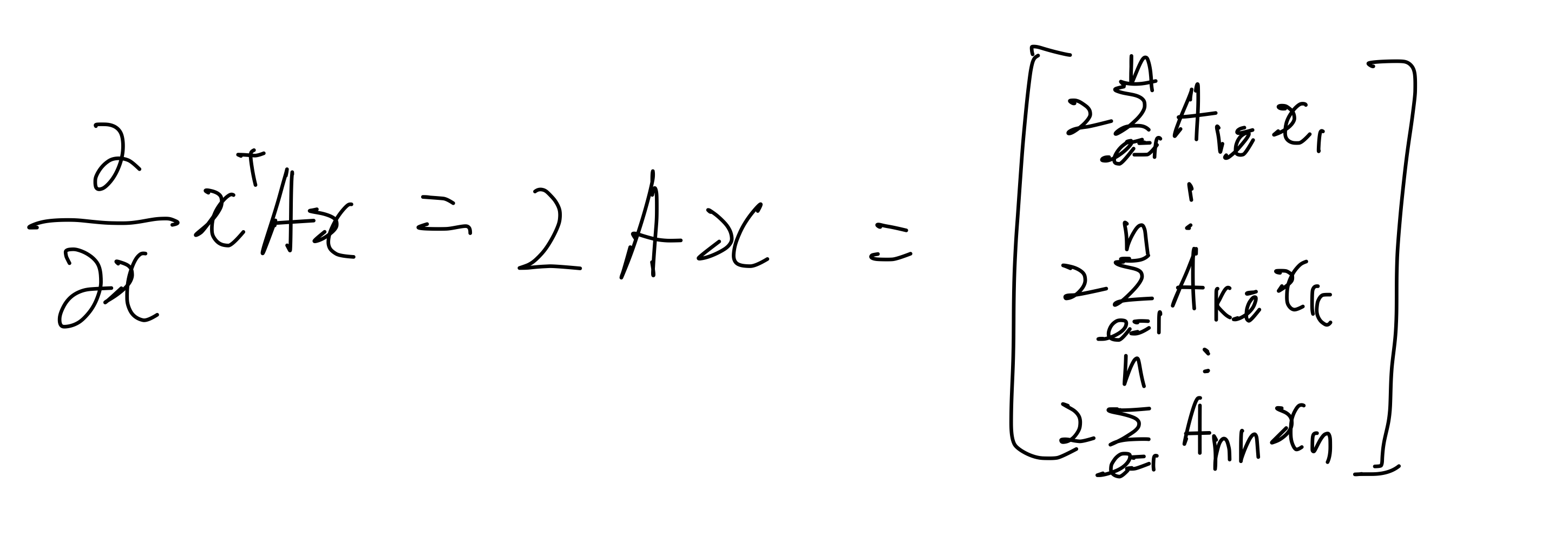
전체 $x$행렬에 대한 미분은 다음과 같이 표현할 수 있다.

한번더 미분을 해보자! 도도함수를 구하는 것과 같다. 행렬의 경우에는 이것을 헤시안 이라고 부른다.

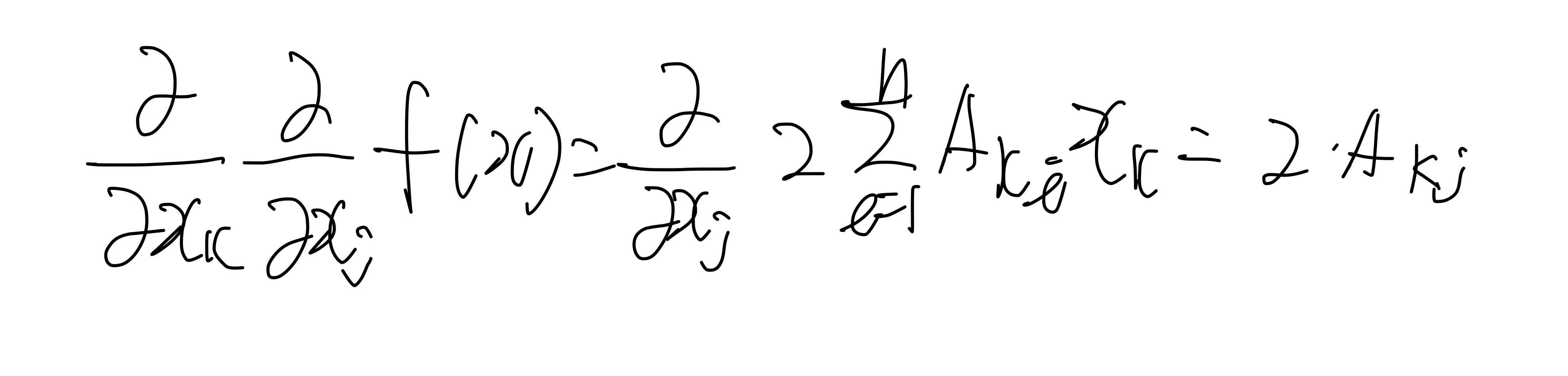
$x_k$ 로 미분 한 것을 $x_j$로 미분 했을 때의 값이다.

이것을 행렬로 표현하면

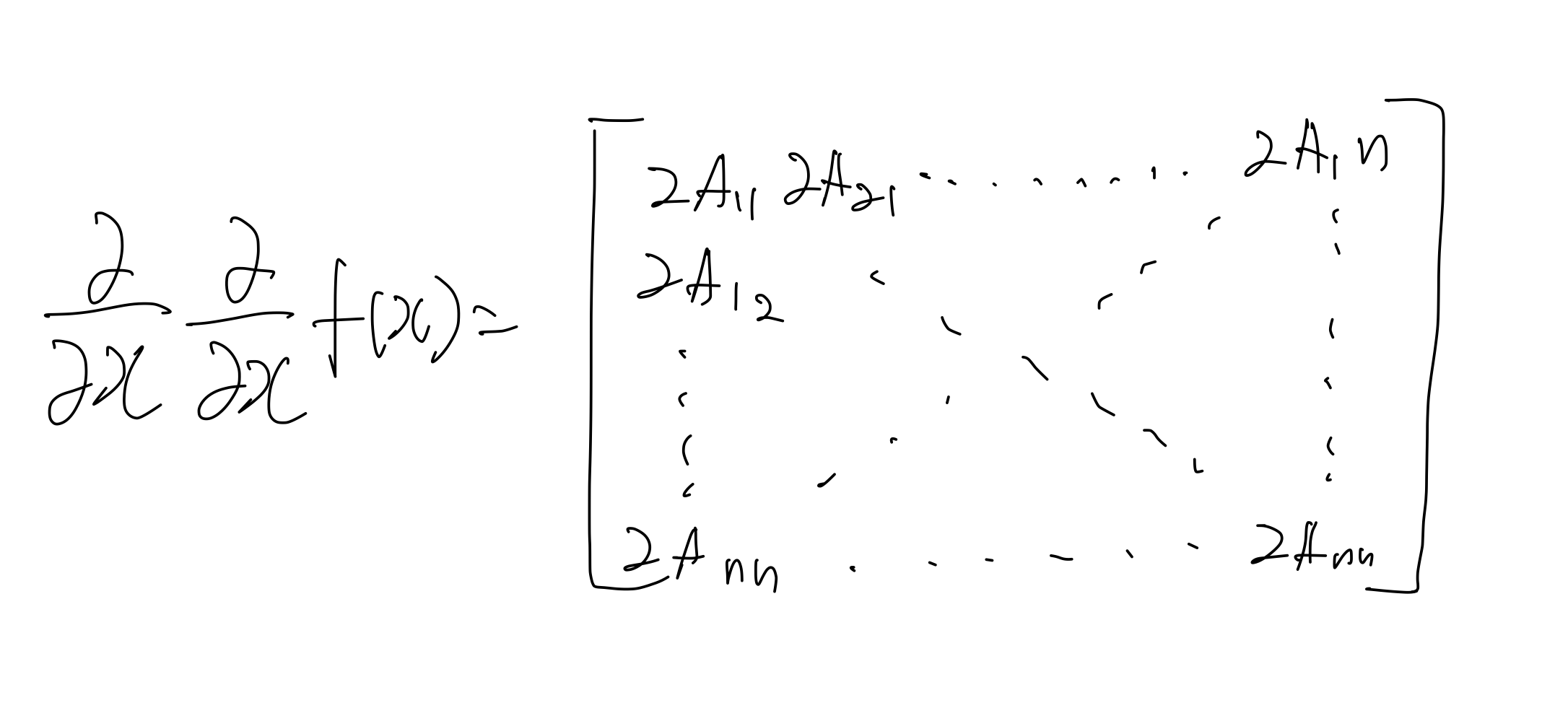
이렇게 표현이 된다.

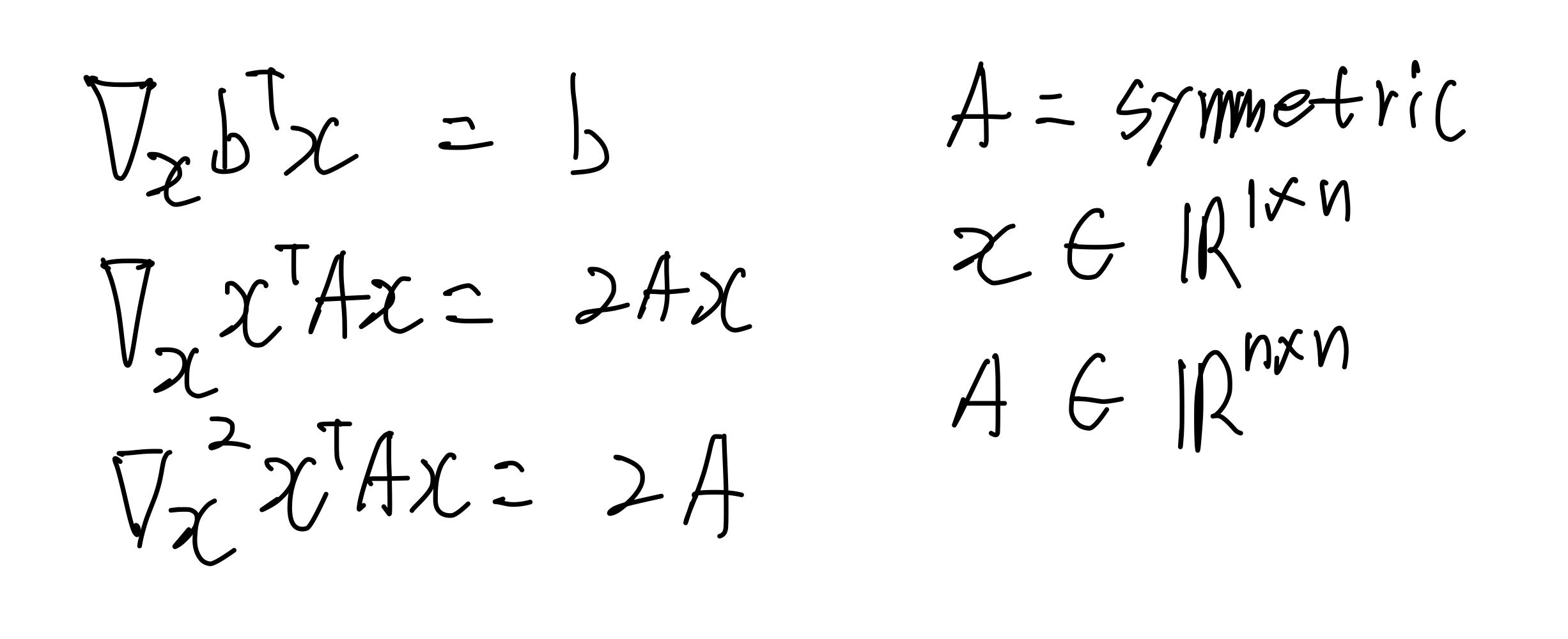
다음과 같은 귀중한 식을 도출할 수 있다.

이제 우리가 2장에서 배웠던 목적함수를 미분해보자.

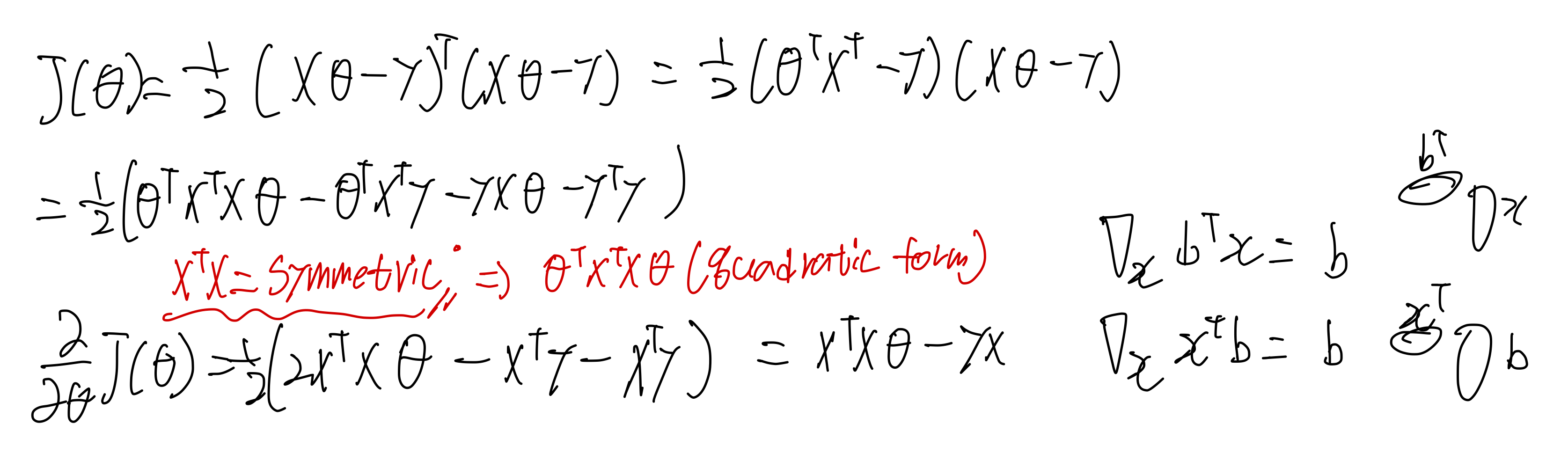
$\frac {\partial} {\partial x} b^\intercal x = \frac {\partial} {\partial x}x^\intercal b = b$ 라는 사실을 유의하자!

이제 도함수를 구했으니 지난 도함수가 0 인 지점을 찾으면 된다.
$X^\intercal X\theta - X^\intercal y =0$
$\theta = (X^TX)^{-1}X^{\intercal}y$