Encoding

인코딩이란 부호화라고도 하며, 사람이 인지할 수 있는 형태의 데이터를 컴퓨터가 이용할 수 있도록 코드화하고 압축하는 것이다.

목적

• 처리 속도 향상
• 데이터 형식 표준화
• 보안
• 저장 공간 절약 등

Decoding

인코딩한 데이터를 원래의 데이터로 변환하는 것을 디코딩(복호화)라고 한다.

Base64

바이너리 데이터를 공통 ASCII 영역의 문자들로만 이루어진 문자열로 변환하는 인코딩 방식이다.

문자열을 ASCII 코드로 변경한 뒤 6bit씩 끊어 변환한다.

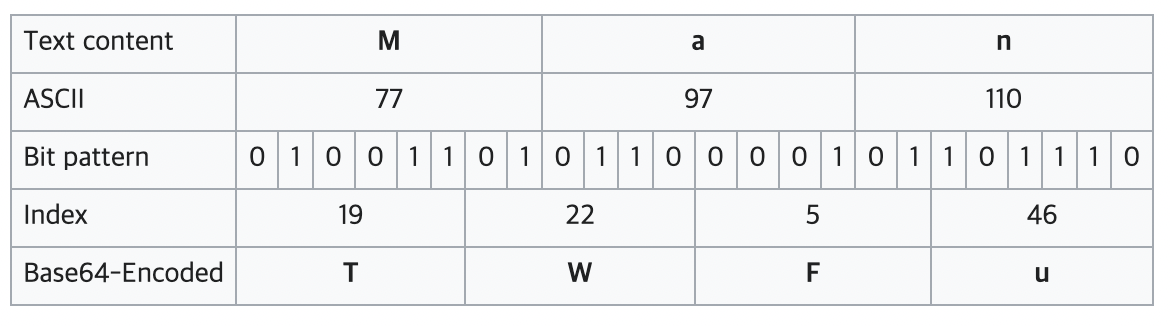
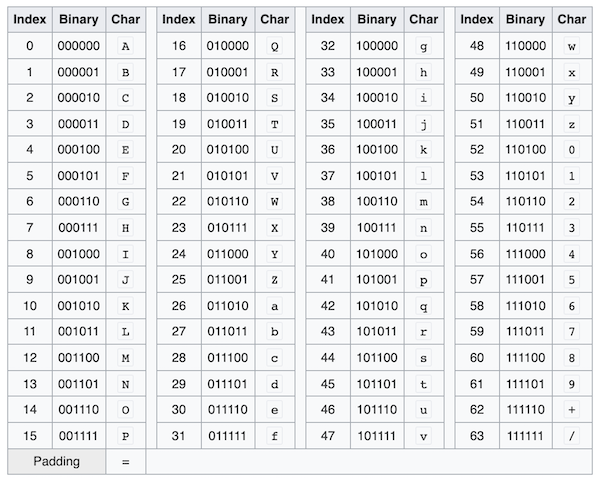
Base64 테이블

Base64 Padding 전략

Huffman coding

고정 길이 코드

ASCII 코드가 대표적이다.
8비트 길이를 고정하기 때문에 저장공간을 차지한다는 단점이 있다.

접두어 코드

다른 코드의 접두어가 되지 않는 코드이다.
00, 010, 100, 101 의 경우 00010100101로 표현이 가능하다. (11bit)

Huffman coding은 문자들의 빈도로부터 접두어 코드를 만들어 내는 알고리즘이다.

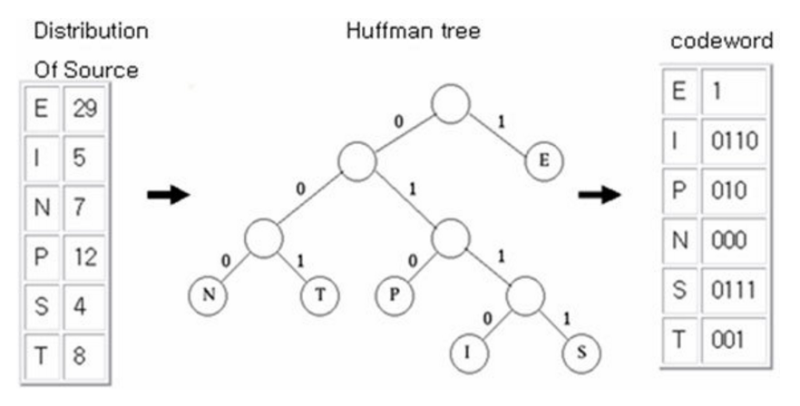
• 빈도 수가 높은 문자에는 짧은 접두어 코드를 부여한다.
• 빈도 수가 낮은 문자에는 긴 접두어 코드를 부여한다.
• 트리의 왼쪽 자식 노드는 0, 오른쪽 자식 노드는 1로
  루트 노드에서 리프 노드(문자가 기록된 노드)까지 가는 경로가 접두어 코드가 된다.

알고리즘

1. 빈도수가 적은 두 노드 삭제
2. 두 노드 중 빈도수 적은 것을 왼쪽으로 하는 노드 삽입
3. 반복

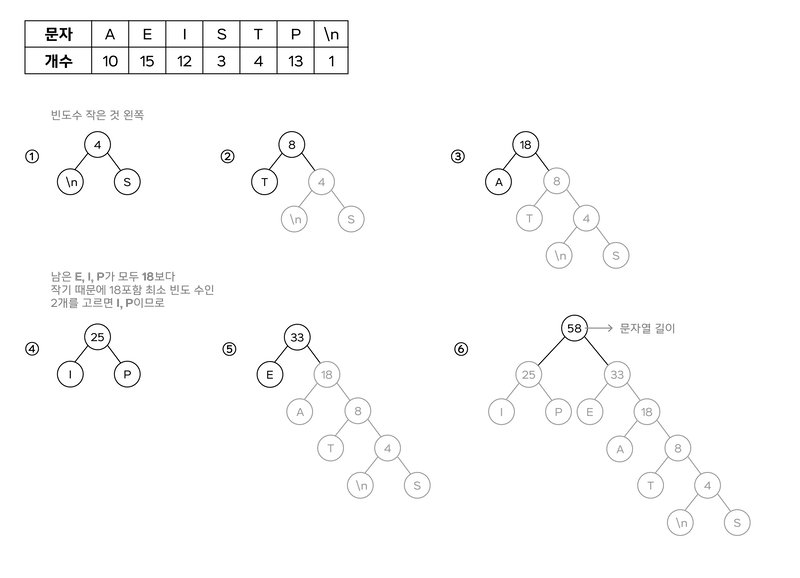
위 사진의 결과는 아래와 같습니다.

A	E	I	S	T	P	\n
110	10	00	11111	1110	01	11110

UTF-8

유니코드를 위한 가변 길이 문자 인코딩 방식 (1~4바이트)
앞에 U+를 붙여 표현한다

코드포인트 범위	인코딩 방법	크기
U+0000 ~ U+007F	그대로	1byte
U+0080 ~ U+07FF	110xxxxx 10xxxxxx	2byte
U+0800 ~ U+FFFF	1110xxxx 10xxxxxx 10xxxxxx	3byte
U+10000 ~ U+1FFFFF	11110xxx 10xxxxxx 10xxxxxx 10xxxxxx	4byte

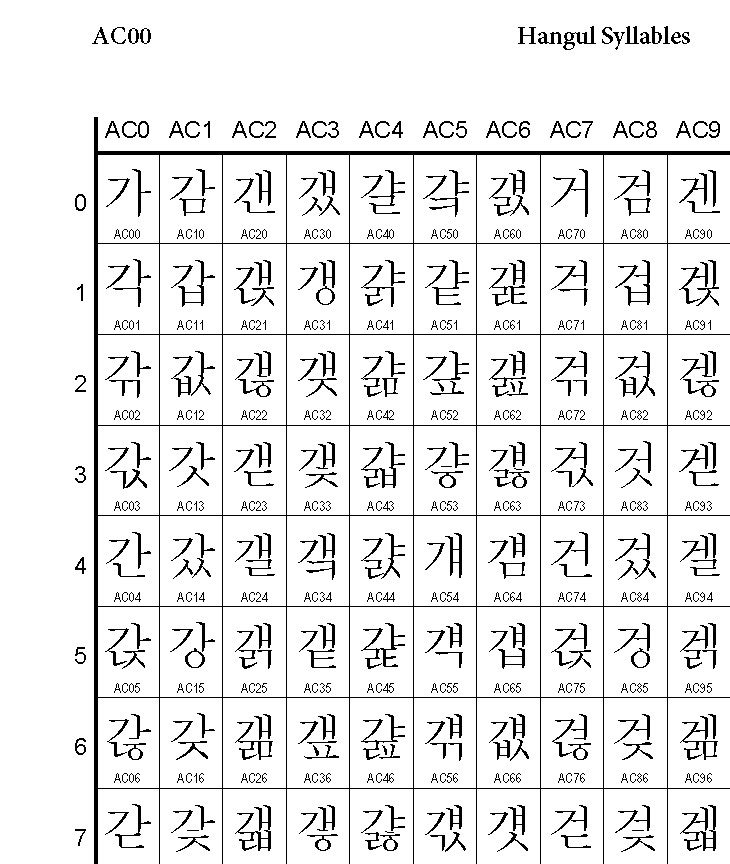
왼쪽의 유니코드 표에서 ‘가'의 코드포인트를 찾아보면 U+AC00이다.
이를 2진수로 표현하면 1010110000000000이다.

U+AC00은 위 표에 나온 인코딩 방법 중
1110xxxx 10xxxxxx 10xxxxxx에 해당한다.

따라서 x의 자리에 2진수를 채우면
11101010 10110000 10000000 (EA B0 80)
이 된다.