[DBMS] B-Tree

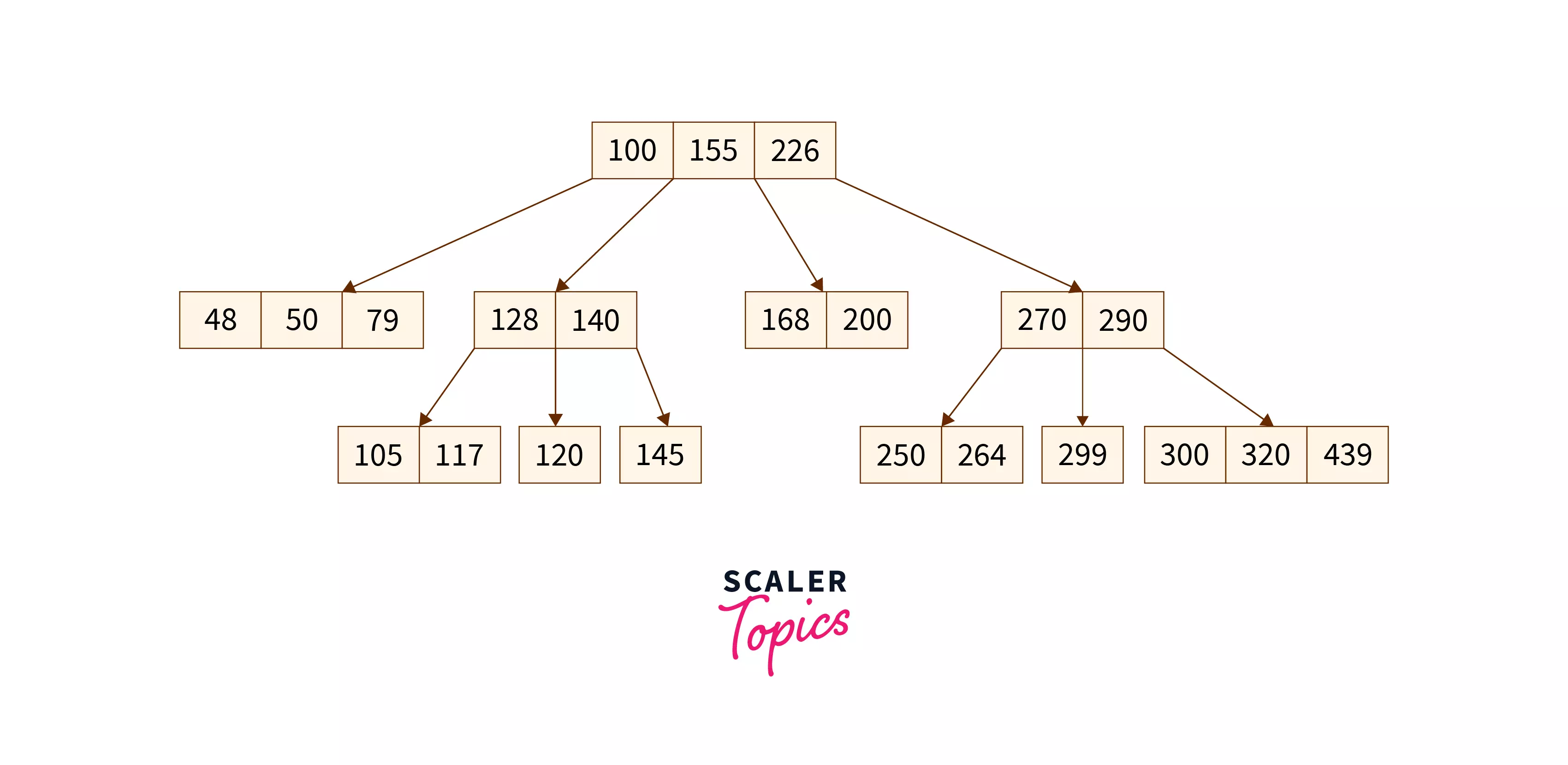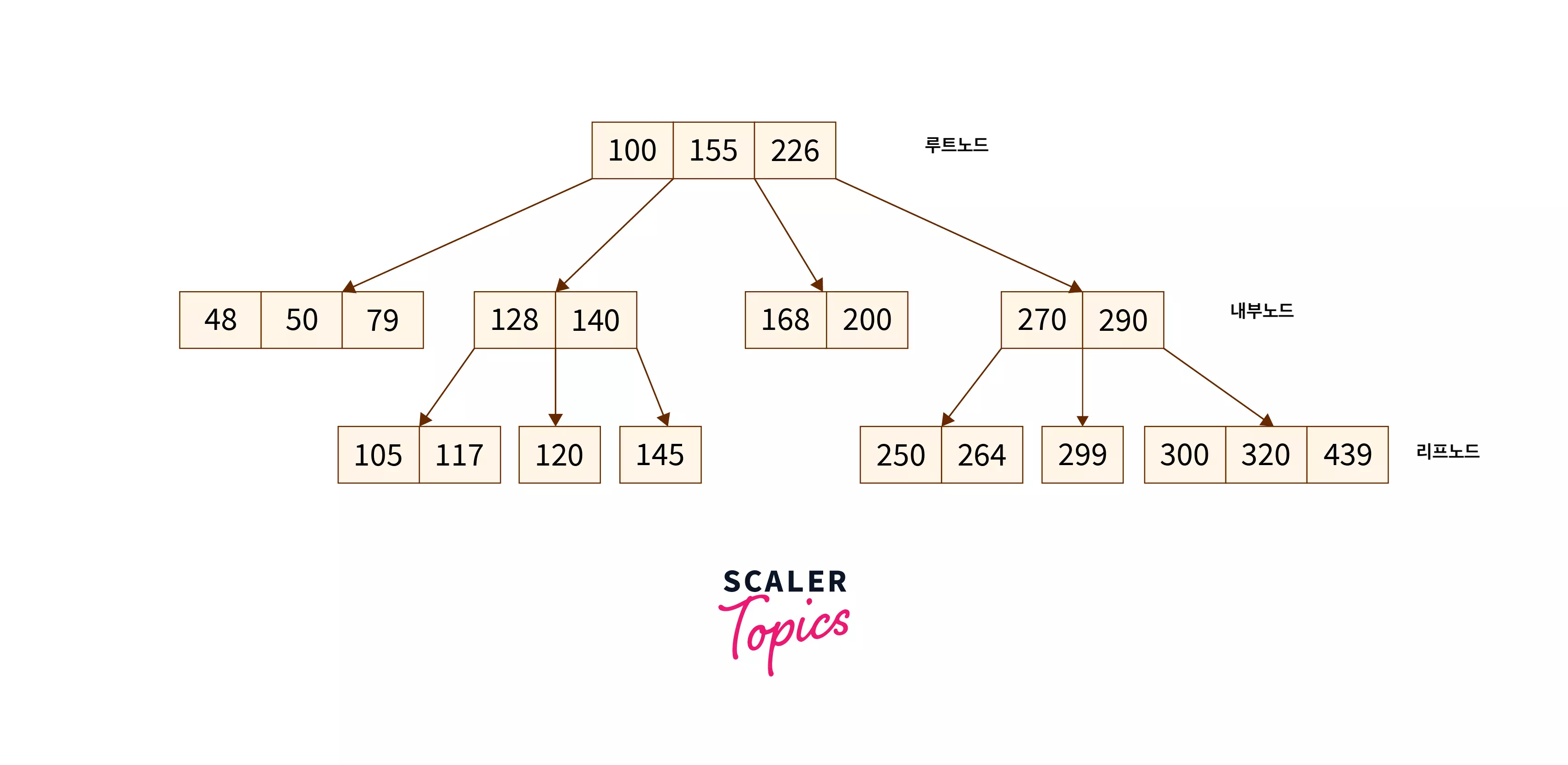
B-Tree

특징

• 각 노드는 키 값과 포인터를 가짐
• 키 값은 오름차순으로 저장됨
• 모든 리프노드는 같은 레벨에 존재함
• 각 노드가 여러 키와 자식 노드를 가질 수 있음
  ➡️ 트리의 높이가 낮으므로 더 빠른 검색이 가능함
• 검색, 삽입, 삭제 모두 O(log N)의 성능

B-Tree vs 이진 트리

1. 노드 구조
   • B-Tree : 각 노드가 여러 키와 자식 노드를 가질 수 있음
   • 이진 트리 : 각 노드가 최대 두개의 자식 노드를 가짐
2. 트리 높이
   • B-Tree : 트리의 높이가 낮아 더 빠른 검색이 가능함
   • 이진 트리 : 자식 노드가 두 개 뿐이므로 트리의 높이가 상대적으로 높음
3. 탐색 경로
   • B-Tree : 탐색 시 노드에서 여러 키를 비교하여 적절한 자식으로 내려감
   • 이진 트리 : 노드 하나의 키를 기준으로 왼쪽 또는 오른쪽 자식으로 이동
4. 균형
   • B-Tree : 항상 균형 잡인 상태를 유지해 검색, 삽입, 삭제 모두 O(log N)의 성능 보장
   • 이진 트리 : 균형 상태를 보장하지 않아 최악의 경우 선형 시간
5. 비교
   • B-Tree : 한 노드에서 여러 개의 키를 비교한 후, 적절한 자식 노드로 이동함. 비교 횟수가 많지만, 트리의 높이가 낮아 전반적인 탐색 성능이 효율적
   • 이진 트리 : 한 노드에서 하나의 키와 비교하고 자식 노드로 이동함. 비교 횟수는 적지만, 트리가 불균형해지면 탐색 성능이 떨어질 수 있음

B-Tree 에서 키 값 비교

• 과정
  1. 새로운 키를 탐색할 때 정렬된 노드의 키 값들과 순차적으로 비교함
  2. 적절한 위치를 찾아 적절한 자식 노드로 내려감

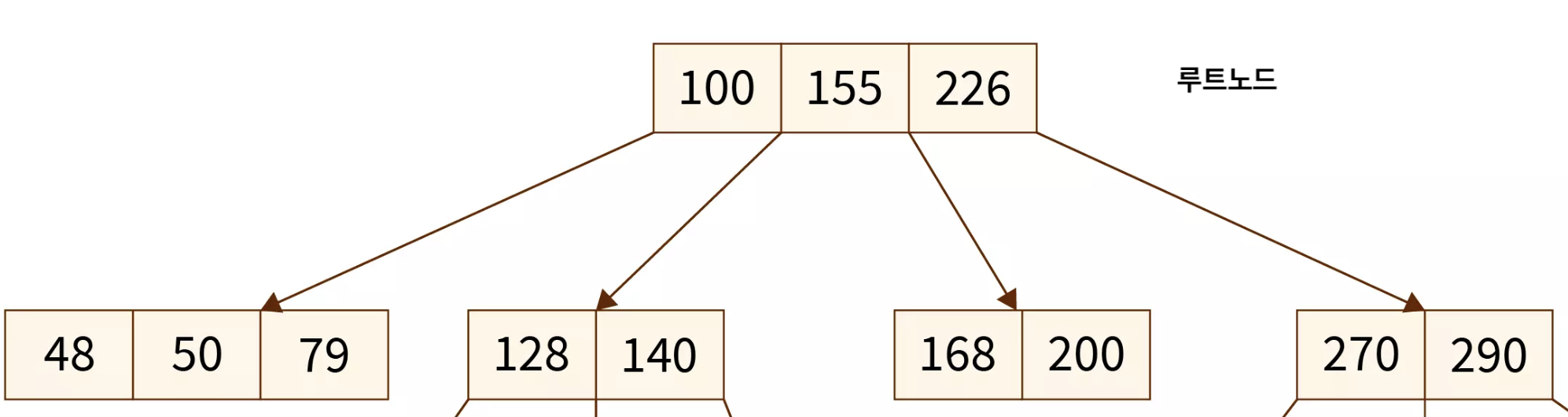
• 예시 : B-Tree 의 한 노드에 [100, 155, 226] 이라는 세 개의 키 값이 있다면 ?
  • 찾으려는 값이 100보다 작으면 ? ➡️ 첫번째 자식으로 이동함
  • 찾으려는 값이 100과 155 사이에 있으면 ? ➡️ 두번째 자식으로 이동함
  • 찾으려는 값이 155와 226 사이에 있으면 ? ➡️ 세번째 자식으로 이동함
  • 찾으려는 값이 226보다 크면 ? ➡️ 네번째 자식으로 이동함

B-Tree 의 삽입 과정

1. 초기 상태
   

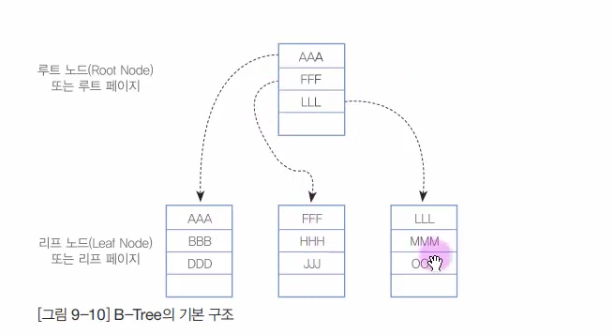
2. III 삽입
   

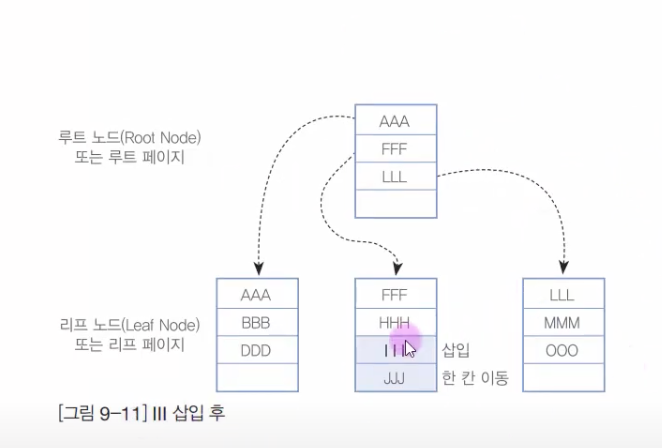
• B-Tree 에서 III 가 삽입될 적절한 노드를 찾음
• JJJ 를 한 칸 이동 후 III 삽입함

3. GGG 삽입
   

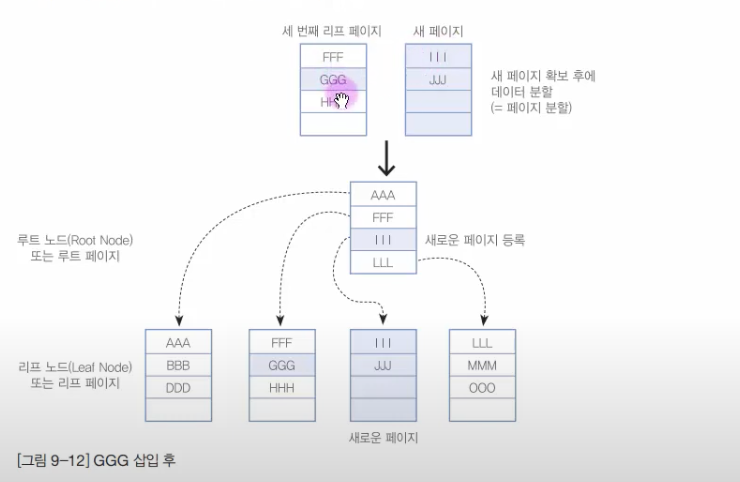
• B-Tree에서 GGG 가 삽입될 적절한 위치를 찾음
• 해당 노드가 Full 상태이므로 적절하게 페이지 분할함
• III 와 JJJ 를 새로운 페이지로 저장함
• III 를 새로운 페이지로 등록함

4. PPP 삽입

• B-Tree에서 PPP 가 삽입될 적절한 위치를 찾음
• PPP 삽입함

5. QQQ 삽입

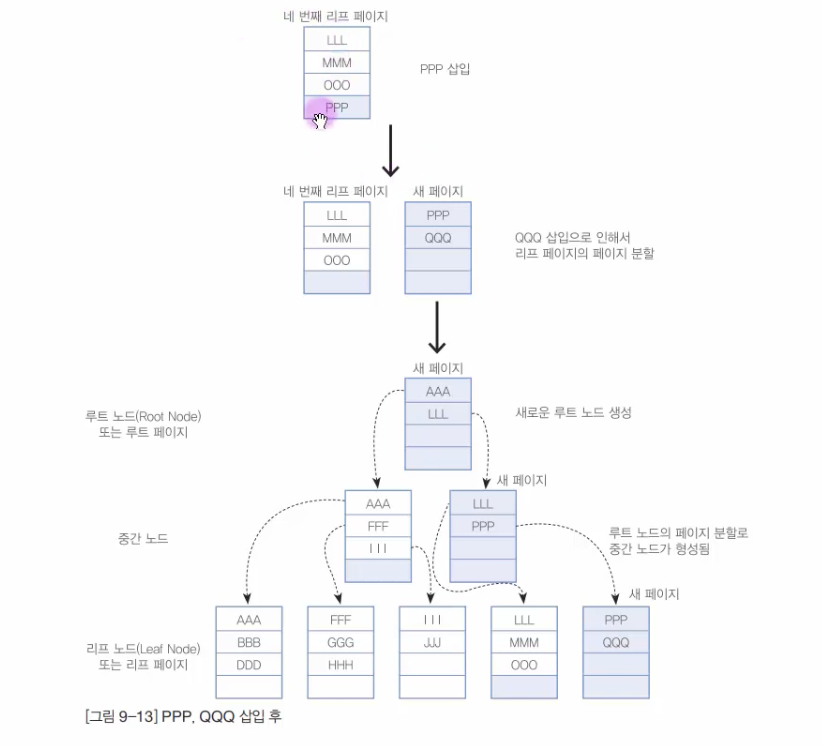
• B-Tree에서 QQQ 가 삽입될 적절한 노드를 찾음
• 해당 노드가 Full 상태이므로 적절하게 페이지 분할함
• PPP 와 QQQ 를 새로운 페이지로 저장함
• 중간 노드가 Full 이므로 페이지 분할하고 PPP 를 새로운 페이지로 등록함