[LeetCode] 909. Snakes and Ladders

https://leetcode.com/problems/snakes-and-ladders

개요

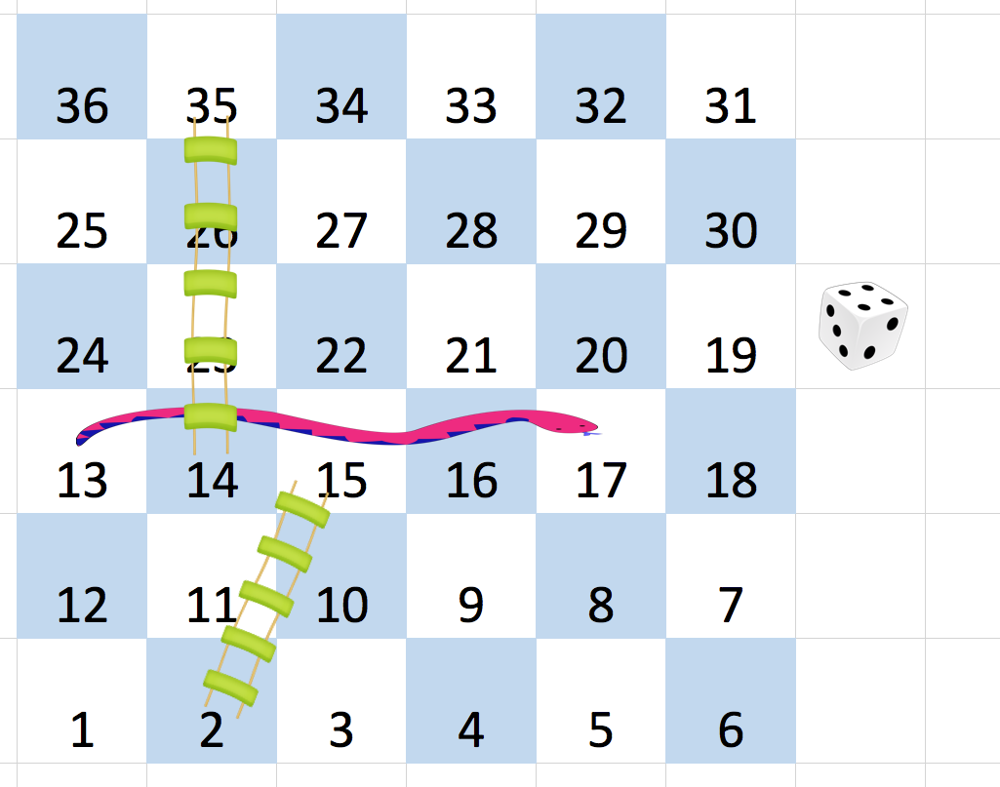
1. 정사각 테이블이 주어진다.
   • 모든 노드가 가진 val은 노드의 인덱스와 동일하다.
   • [n-1][0] 컬럼이 1번 컬럼이고, n^2번 컬럼은 Boustrophedon 규칙에 의한 컬럼이다.
2. 1번 컬럼에서 n^2번 컬럼으로 이동할 때 최소 이동 횟수를 반환해라.
   • n^2번 컬럼에 도달할 수 없는 경우 -1을 반환하라
3. 각 컬럼에서 이동 가능한 범위는 (컬럼 인덱스 + 1, 컬럼 인덱스 + 6) 이다.

문제 해결 아이디어

• 아래와 같이 Boustrophedon 규칙을 따른다.
  ➡️ 해당 규칙에 맞게 인덱스를 재정의하자.
  ➡️ 새로운 인덱스로 board에 해당하는 인덱스를 참조할 수 있게 하자. ex> (새로운 인덱스, board 내 인덱스)
  
• 각 컬럼에서 이동 가능한 범위와 경우의 수는 정해져 있다.
  ➡️ 그래프에서 이웃이 결정되어 있는 구조를 떠올릴 수 있다.

🧐 그래프 BFS를 이용하자

의사 코드

1. do Boustrophedon 규칙에 맞게 새로운 인덱스를 만든다.
2. 큐에 인덱스를 삽입한다.
3. 맵에 <인덱스, 1번 인덱스로부터 거리>를 삽입한다.
4. 큐에서 인덱스를 하나 빼온다.
5. 현재 인덱스로부터 이동 가능한 범위 (인덱스 + 1, 인덱스 + 6) 를 순회한다. (반복)
6. 이동할 인덱스가 snake나 ladder에 해당한다. (분기)
   6-1. (true) 이동할 인덱스 = snake or ladder
   6-2. (false) 이동할 인덱스 = 원래 인덱스
7. 맵이 이동할 인덱스를 키로 갖고 있지 않다. (분기)
   7-1. (true) 맵에 <이동할 인덱스, 1번 인덱스로부터 거리>를 삽입한다.
   7-2. (true) 큐에 이동할 인덱스를 삽입한다.

do 인덱스 to Boustrophedon 인덱스

while(큐가 비어있지 않음){
	int 현재인덱스 = 큐.poll();
    
    if(현재인덱스 == n * n) return map.get(현재인덱스)
    
    
    for(i = 1 to i <= 6){
    	int 다음인덱스 = 현재인덱스 + i;
        if(board[다음인덱스] != -1) next = board[다음인덱스]
        if(!map.containsKey(다음인덱스)){
     		int 현재인덱스까지최소이동거리 = map.get(현재인덱스);
        	map.put(다음인덱스, 현재인덱스까지최소이동거리 + 1);
           	q.offer(다음인덱스)
        }
        
    }
  
}

실제 코드

public static int snakesAndLadders(int[][] board) {
        // 인덱스 처리
        int n = board.length;
        int[][] indexes = new int[n * n + 1][2]; // 인덱스 : [x, y]
        int index = 1;
        boolean isForward = true;

        for (int i = n - 1; i >= 0; i--) {
            if (isForward) {
                for (int j = 0; j < n; j++) {
                    indexes[index][0] = i;
                    indexes[index][1] = j;
                    index++;
                }
                isForward = false;
            } else {
                for (int j = n - 1; j >= 0; j--) {
                    indexes[index][0] = i;
                    indexes[index][1] = j;
                    index++;
                }
                isForward = true;
            }
        }


        Queue<Integer> q = new LinkedList<>();
        Map<Integer, Integer> distances = new HashMap<>();


        int cur = 1;
        q.offer(cur);
        distances.put(cur, 0);
        while (!q.isEmpty()) {
            cur = q.remove();

            int distance = distances.get(cur);
            if (cur == n * n) return distance;
            for (int i = 1; i <= 6; i++) {
                int next = cur + i;
                if (next > n * n) break;
         
                int r = indexes[next][0];
                int c = indexes[next][1];
                if (board[r][c] != -1) {
                    next = board[r][c];
                }


                if (!distances.containsKey(next)) {
                    distances.put(next, distance + 1);
                    q.offer(next);
                }
            }
        }

        return -1;

    }

결과

전체 코드 github 링크

다른 풀이

public int snakesAndLadders(int[][] board) {
        int boardLength = board.length;
        int boardArea = boardLength * boardLength;
        int[] flatten = new int[boardArea];
        boolean[] visisted = new boolean[boardArea];

        boolean right = true;
        int counter = 0;
        // flatten the board into a single dimension
        for (int y = boardLength - 1; y >= 0; y--) {
            for (int x = 0; x < boardLength; x++) {
                int actualX = right ? x : boardLength - 1 - x;

                flatten[counter] = board[y][actualX];
                counter++;
            }
            right = !right;
        }

        int moves = 0;
        Queue<Integer> q = new LinkedList<>();
        q.add(0);
        q.add(null);

        while (!q.isEmpty()) {
            Integer current = q.poll();

            // if null and there are more elements increment and add another null
            if (current == null) {
                if (!q.isEmpty()) {
                    q.add(null);
                    moves++;
                }
            } else {
                // we made it to the end, because this is BFS we can assume this is the best case since we take the values layer by layer
                if (current == boardArea - 1) {
                    return moves;
                }

                // loop through current + 1 to current + 6 or the end of the board
                for (int i = current + 1; i <= Math.min(current + 6, boardArea - 1); i++) {
                    // if the current space has something other than -1 replace with the actual move
                    int actualMove = flatten[i] == -1 ? i : flatten[i] - 1;

                    if (visisted[actualMove]) continue;
                    visisted[i] = true;
                    visisted[actualMove] = true;
                    q.add(actualMove);
                    
                }
            }
        }


        return -1;
    }

이 문제를 풀면서 가장 고민한 부분은 Boustrophedon 테이블이라는 인덱스 규칙의 특이한 부분을 어떻게 표현할지였다.
나는 그래서 isForword 플래그를 만들어서 해당 두가지 경우에 대한 분기로 For 문을 두 개 정의했다.
그런데 이 풀이는 그렇게 하지 않고 동일한 For문 내에서 연산 규칙을 활용하는 방법으로 풀이했는데, 매우 좋은 배울 점인 것 같다.
나도 이 부분을 꼭 기억해서 다음에 이런 풀이가 필요하면 비슷하게 구현해봐야겠다.

나눗셈 연산으로 표현하기 어려워서 인덱스 규칙을 재구현한것이기 때문에, 나는 이런 풀이가 바람직하지 못한 부분인 줄 알았는데 평탄화 라는 이름도 붙여져 있는 스킬이었다..!
평탄화에 대해 좀 더 알아보고 꼭 머릿속에 담아둬야겠다.