[백준 7576] 토마토

문제 바로가기

문제 분류

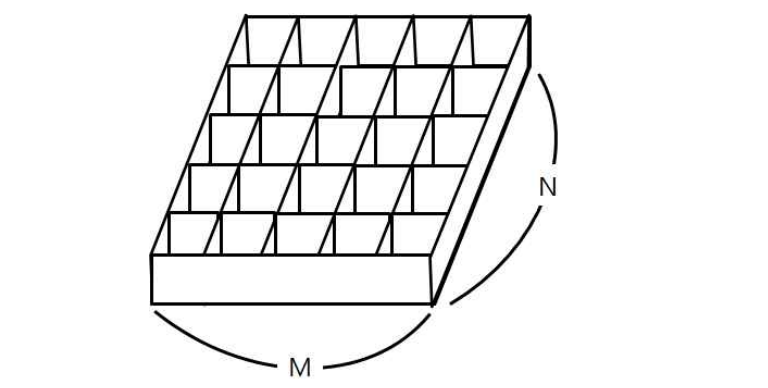
가중치가 없는 그래프에서 다중 시작점에서부터 모든 칸까지의 최단 거리를 구하는 문제
출처 - https://solved.ac/contribute/7576

bfs

알고리즘

1. 익은 토마토의 위치를 queue에 삽입
2. queue의 익은 토마토들을 dfs로 순회하며 주변의 안익은 토마토를 익음 처리하고 queue에 삽입. 순회할 때마다 날짜 변수 date를 갱신한다.
3. date를 반환

Time Complexity: $O(mn)$
Space Complexity: $O(mn)$

from collections import deque

m, n = map(int, input().split())
board = []
for i in range(n):
    board.append(list(map(int, input().split())))


def dfs(r_len, c_len, board, q):
    date = -1
    while q:
        date += 1
        same_depth = len(q)
        for i in range(same_depth):
            r, c = q.popleft()
            for r_next, c_next in [(r - 1, c), (r, c + 1), (r + 1, c), (r, c - 1)]:
                if 0 <= r_next < r_len and 0 <= c_next < c_len and board[r_next][c_next] == 0:
                    board[r_next][c_next] = 1
                    q.append((r_next, c_next))
    return date


def solution(m, n, board):
    for row in range(n):
        if 0 in board[row]:
            break
    else:
        # 이미 다 익어있는 경우
        return 0

    q = deque()
    for row in range(n):
        for col in range(m):
            if board[row][col] == 1:
                q.append((row, col))

    answer = dfs(n, m, board, q)

    for row in range(n):
        if 0 in board[row]:
            # 토마토가 모두 익지는 못하는 상황
            return -1
    return answer


print(solution(m, n, board))