Non-Local Neural Networks 논문 정리

이번에 리뷰해볼 논문은 작년 초쯤에 읽었지만 사실 그때가 학기중이었어서 거의 이해를 하지 못했던 Non-local Neural Network이다.

---

1. Introduction

Neural network에서 주로 많이 사용하는 network의 종류에는 recurrent neural network와 convolutional neural network가 있다. 사실 computer vision 관련 모델에서 convolution 연산을 하지 않고 만들어져있는 네트워크 구조는 찾아보기 어렵다. 마찬가지로 RNN 역시 굉장히 많은 아키텍쳐에서 자주 쓰이는 기본 연산 중 하나이다.

하지만 두 연산 모두 근본적인 한계를 가지고 있는데, local neighborhood만 processing하는 연산이라는 것이다. CNN을 생각해보면, 아무리 atrous convolution이나 큰 kernel size를 사용하더라도 필터가 한번에 볼 수 있는 영역은 제한적이다. (물론 3x3 conv filter로도 충분하다고는 하지만..) 그리고 RNN의 경우에도 바로 이전의 시간만 볼 수 있다. (gateway나 memory cell을 쓸 수는 있지만)

이렇게 시간축, 또는 공간축으로 local한 정보만 알 수 있는 operation들은 보통 global하게 보기 위해서 반복적으로 연산을 수행한다. (7x7 conv나 9x9 conv 대신 3x3 conv 여러개 쓰는 것 처럼) 하지만 이런 반복 연산들도 문제를 가지는데, 일단 global한 영역을 보기 위해서 반복연산을 수행하기 때문에 비효율적이고, 최적화하기도 힘들며, 모델링할 때 multi-hop dependency가 생긴다.

그래서, 이 논문에서는 non-local means filter를 응용한, long-range dependency 문제를 해결할 수 있는 새로운 operation을 제안한다. Non-local operation은 input feature map에서의 모든 position의 feature를 weighted sum 형태로 더해준다.

이런 non-local neural operation을 사용하면 굉장히 많은 장점이 존재하고, 비디오 분류 문제에서는 2D나 3D convolutional network보다 더 좋은 성능을 보인다. 그리고 비디오 분류 문제 뿐만 아니라 object detection / segmentation, pose estimation 문제에도 이 operation을 적용하면 성능이 전반적으로 향상되기 때문에, 이 operation이 generality를 가진다는 것도 증명할 수 있다.

2. Non-Local Neural Networks

1) 장점 및 설명

• 기존의 RNN이나 CNN과는 다르게, 임의의 두 포인트의 interaction을 계산하기 때문에 long range dependency를 직접적으로 계산할 수 있다.
• 기존의 필터들 처럼 굳이 중첩해서 쌓을 필요가 없기 때문에 레이어 조금만 있어도 성능이 좋은 효율적인 네트워크이다.
• input size를 유지하고, 다른 operation과의 결합이 쉽게 때문에 확장성이 좋다.

상단의 수식에서 볼 수 있듯이, output $y$의 position $i$는 input x의 position $i$와, 다른 모든 position들에 대해서 계산된 결과이다. 말이 너무 이상한 것 같은데 여기에서 제일 중요한거는 $\forall j$ 와 같이 모든 다른 position에 대해서 계산한다는 점이다. CNN처럼 근처 몇개의 픽셀이나, RNN처럼 시간축으로의 최근 몇 개만 보는게 아니라 모든 position을 고려할 수 있는 연산이다. 그리고 모든 position에 대한 연산을 하지만 fc와도 다른점이, fc는 단순 weight을 학습할 뿐이지만 이 연산은 다른 location간에 relationship을 학습할 수 있다.

그리고 $f$는 pairwise function으로 position x와 y와 관계를 계산하고, unary function $y$는 position j에서의 representation을 계산한다. 그리고 모든 position에 대한 연산 값을 더해서 normalize factor로 나눠준다.

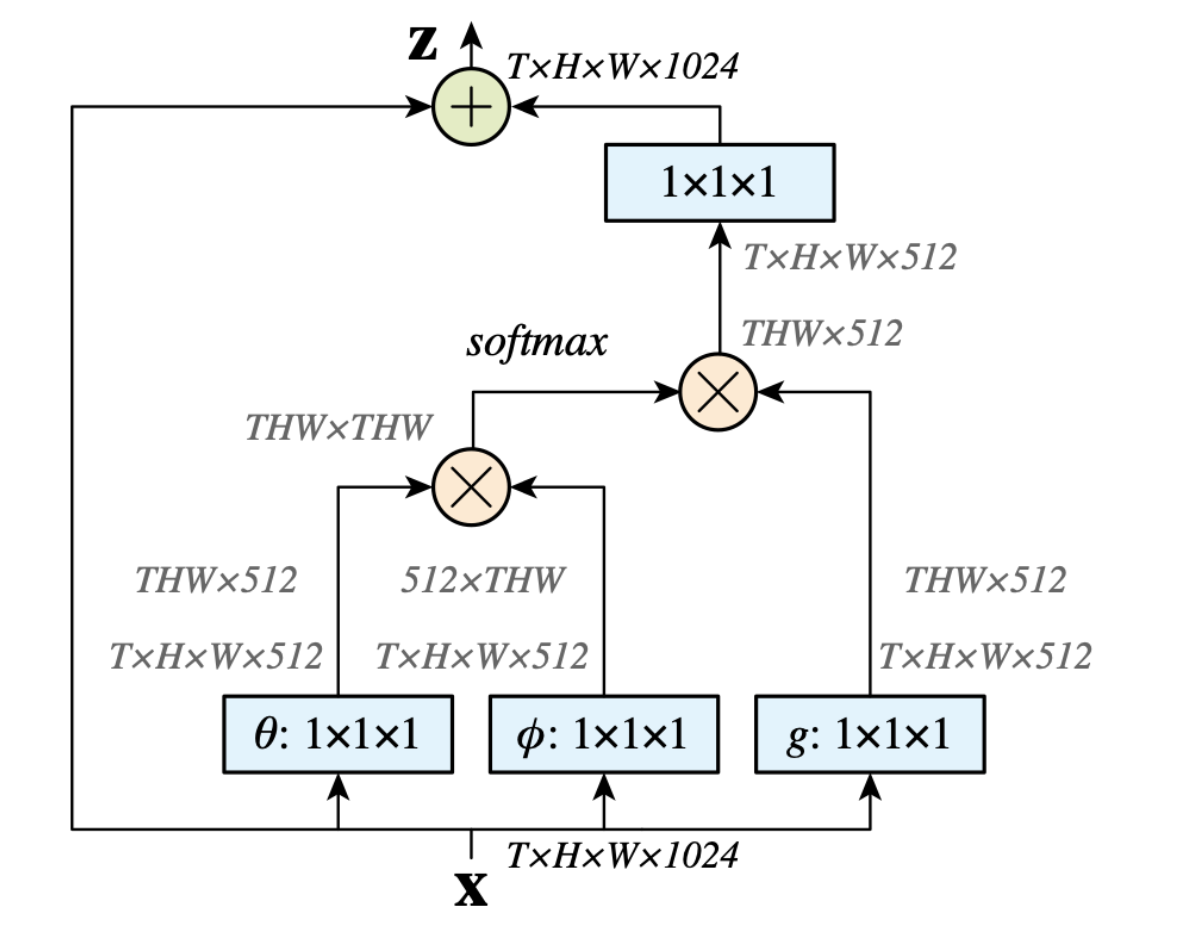
Time 축까지 고려한 non-local block 도식화이다. 시간축을 고려하지 않으려면 $T$를 빼면 된다. 아래에서 다양한 $f$와 $g$에 대해서 고려할텐데, 그 중 embedded Gaussian 버전이다.

2) Instantiations

pairwise function $f$와 unary function $g$는 다양한 버전이 있다. 하지만 어떤 버전을 사용하던지 성능은 그렇게 크게 변하지 않고, 중요한 것은 non local behavior 그 자체라고 한다.

Pairwise function $f$ 비교

$f$만의 성능 변화를 제대로 관찰하기 위해서, unary function $g$를 $g(x_j) =W_g x_j$로 고정했다. 여기에서 $W$는 learnable weight matrix로 1x1 convolution, time 축이 껴있으면 1x1x1 convolution이다.

• Gaussian - $f(x_i, x_j) = e^{{x_i}^T x_j}$

여기에서 $e^{{x_i}^T x_j}$ 은 dot-product similarity를 의미한다. 물론 Euclidean distance를 사용할 수도 있겠지만, 딥러닝에서 dot product를 더 많이 쓰고 구현하기도 쉬워서 선택했다고 한다.

• Embedded Gaussian - $f(x_i, x_j) = e^{\theta({x_i})^T \phi(x_j)}$

앞의 Gaussian에서 조금 더 확장을 하면 Embedded Gaussian이 되는데, 이 Embedded Gaussian의 special case가 self attention module이라고도 해석할 수 있다고 한다. 이 버전에서 연산이 어떻게 수행되는 지는 위에 그림으로 자세하게 나와있다.

• Dot product - $f(x_i, x_j) = \theta({x_i})^T \phi(x_j)$

위의 Embedded Gaussian과 비슷해보이지만, 가장 큰 차이점은 softmax function의 유무라고 한다..!

• Concatenation - $f(x_i, x_j) = ReLU({w_f}^T \lbrack \theta({x_i}), \phi(x_j) \rbrack)$

여기에서 $\lbrack \quad \rbrack$ 은 concat 연산을 의미한다.

3) Non-local Block

저자는 Non-local operation이 다른 아키텍처에도 쉽게 더해질 수 있도록 하기 위해서 non-local operation을 한단계 wrap up한 Non-local Block을 만들었다.

$y_i$는 아까 위에서 나왔던 $y_i =\frac { 1 }{ \complement (x) } \sum _{ \forall j }f(x_i , y_i)g(x_j)$ 에서의 $y_i$ 이고, $+x_i$는 residual connection을 의미한다.

residual connection이 있어서 이 non-local block을 이미 학습된 모델이라도 중간중간에 끼워 넣을 수 있다. 그리고 pairwise로 계산하는 것도 high-level, sub-sampled feature map에서는 그렇게 연산량이 크지 않다고 한다.

3. Experimental

non-local network가 동영상 데이터에서 어느어느 부분이 높은 관련을 가지고 있는지 시각화 한 것이다. 상단의 표는 다양한 실험 결과를 보여준다. 제일 먼저 (a) instantiations에서는 아까 언급했던 다양한 pairwise function들이 최종 성능에 있어서 그렇게 큰 차이를 보이지 않음을 알려준다. 그리고 (b) ~ (d)는 각각 어느 스테이지에 block을 더하는게 좋을지, 더한다면 몇개를 더하는게 좋을지, 시간축/공간축/시공간축 중 어디에 더하는게 좋을지 실험 비교를 하고 있다.

4. Conclusion

이 논문에서는 long-range dependency를 잡을 수 있는 새로운 non-local operation을 제안한다. 이 operation을 wrap up한 block은 기존에 학습되어 있는 네트워크의 중간중간에 들어갈 수 있으며, 이미 학습되어있는 baseline network에 이 block을 더했을 때 유의미한 성능향상이 있었음을 확인할 수 있었다.

(+ 포스트를 쓰는 절반 이상의 시간을 아마 수식쓰는데 쓴 것 같다.. 그래도 작년에 읽었을 때보다는 이해가 잘 돼서 좋았다..! )

Reference

• https://arxiv.org/abs/1711.07971