해당 포스팅은 '트리' 및 '이진 트리' 자료구조에 대한 이해를 전제로 합니다.
이진 탐색 트리 등장 배경
이진 탐색 : 탐색 시간복잡도 O(logN), 삽입이나 삭제 불가능
연결 리스트 : 탐색 시간복잡도 O(N), 삽입이나 삭제 시 O(1) 소요
이 둘의 장점을 챙긴 자료구조가 이진 탐색 트리이다. 탐색 효율을 높이고 자료의 삽입과 삭제도 가능케 하는 것이 핵심이다.
이진 탐색 트리는 트리 구조로써 한 노드가 자신보다 작은 값을 가진 노드와 자신보다 큰 값을 가진 노드를 가지는 구조를 갖게 된다.
이진 탐색 트리의 특징
- 각 노드의 자식이 2개 이하
- 각 노드의 왼쪽 자식은 부모보다 작고, 오른쪽 자식은 큼
- 부모 노드의 왼쪽과 오른쪽 서브트리도 이진 탐색 트리
- 모든 노드는 유일한 키를 갖게 됨 → 검색 목적 자료구조이므로
.png)
이진 탐색 트리를 순회할 땐 중위순회 방법을 사용하는데, 중위순회를 하게 되면 결국 정렬된 일련의 데이터가 나오게 된다. 위 예시의 경우 중위 순회 결과가 '3-7-12-18-26-27-31' 이 나오는데, 이는 정렬된 데이터임을 알 수 있다.
이진 탐색 트리의 연산
검색
타겟 데이터가 존재하는 지
찾고자하는 값과 현재 루트 노드의 값 비교
→ 타겟 값이 더 크다면 오른쪽 서브 트리로
→ 타겟 값이 더 작다면 왼쪽 서브 트리로
위 로직을 재귀적으로 반복 수행하여, 루트 노드의 값이 타겟 데이터일 때 까지 탐색한다.
삽입
원하는 데이터를 삽입
- 새로운 데이터가 들어갈 자리가 비어있으면 그대로 값을 대입하면 됨
- 비어있지 않은 경우 해당 자리의 노드 값과 비교
→ 삽입할 데이터보다 작다면 왼쪽 자식트리로 이동시키고
→ 삽입할 데이터보다 크다면 오른쪽 자식 트리로 이동하면 된다.
삭제
타겟 데이터를 삭제
중간에 있는 노드를 삭제하는 경우 트리가 중간에 끊기는 등의 상황이 발생할 수 있기 때문에 이를 처리하는 방안이 있어야 한다. 삭제는 세 가지 경우가 있을 수 있는데, 이에 따라 다르게 대처한다.
1. 리프 노드를 삭제하는 경우
→ 그냥 삭제하면 됨
2. 자식 노드가 하나인 노드를 삭제하는 경우
→ 해당 자식 노드를 삭제할 노드의 위치로 끌어올림
3. 자식 노드가 두 개인 노드를 삭제하는 경우
→ 오른쪽 서브 트리의 MIN 값 OR 왼쪽 서브 트리의 MAX 값 중 하나를 삭제할 노드의 위치로 끌어올림
이진 탐색 트리의 연산 시간 복잡도
이진 탐색 트리의 세 개 연산 (검색, 삽입, 삭제) 는 결국 트리를 순회하며 타겟 데이터의 위치를 찾는 연산이 공통적으로 필요하므로, 트리의 높이에 비례하여 시간 복잡도가 증가 하게 된다.
따라서 균형적으로 생성되어 있는 트리의 높이를 H 라고 한다면 H 에 비례하여 O(H) 시간 복잡도를 가지게 되는데, 이는 O(logN) 이라고도 표기할 수 있다. 이유를 살펴보자,
모든 노드가 빈 자리 없이 꽉꽉 채워져있는 이진 탐색 트리를 포화 이진 탐색 트리라고 하는데, 이렇게 트리가 구성되어 있는 경우가 가장 최적의 상황이다.
포화 이진 탐색 트리를 구성하고 있는 노드의 개수를 N 이라고 했을 때, 트리 높이와의 관계는 다음과 같다.

따라서 노드의 개수를 통해 아래와 같이 트리의 높이를 계산할 수 있다.
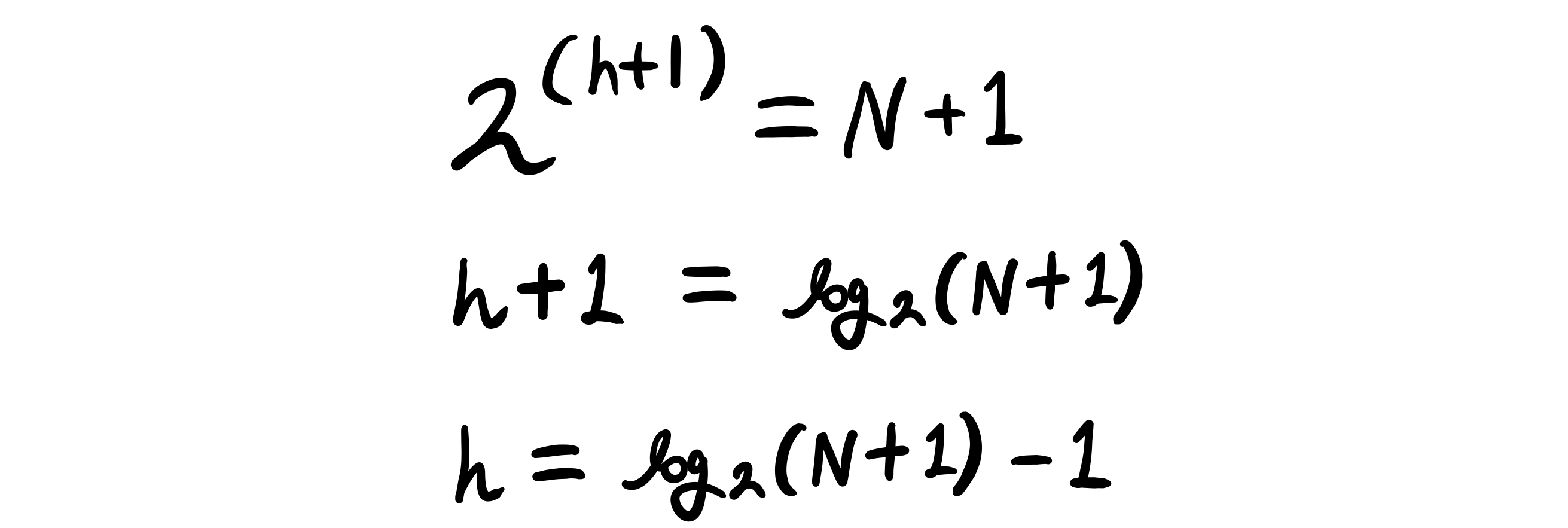
H = log2(N + 1) - 1라는 식을 유도해낼 수 있다.
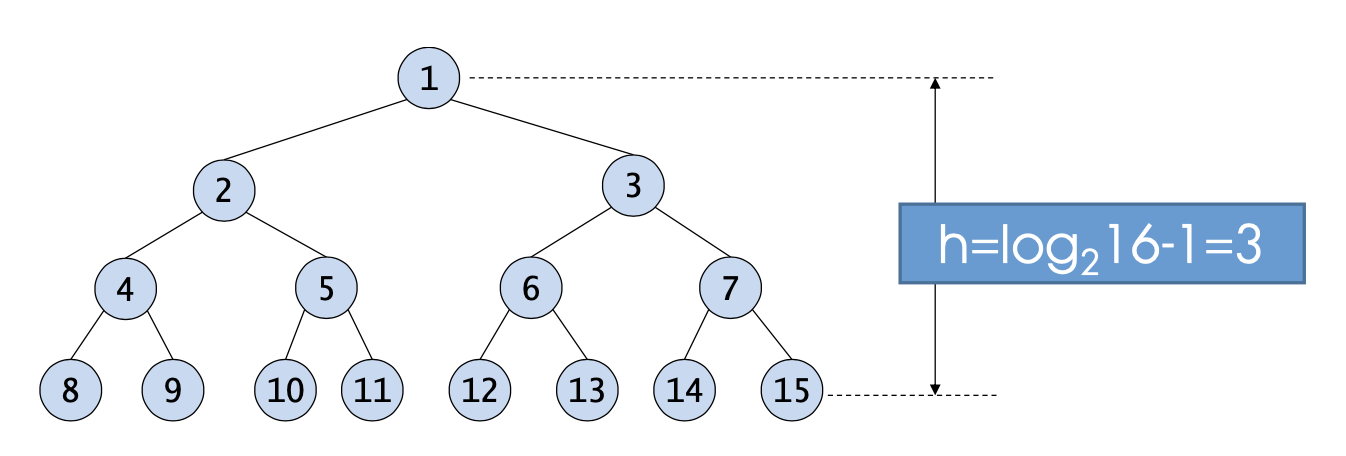
위 예제 사진을 보면, 노드의 개수가 15개이다. 아까 H = log2(N + 1) - 1 식에 '15'를 대입해보자. 계산 결과는 '3'이고, 예제에서 보이는 트리의 높이와 같다.
이진 탐색 트리의 검색, 삽입, 삭제는 트리의 높이에 비례하여 시간 복잡도가 증가한다고 했다. 따라서, 이를 일반적인 Big-O 시간 복잡도로 표현하자면 위 식을 간소화한 O(logN) 으로 표현할 수 있는 것이다.
.png)
