#Hash #HashTable #HashCollision

H43RO·2021년 10월 4일

CS Chaining Hash Collision HashMap HashTable Hashing Open Addressing hash function 자료구조

CS 뿌셔먹기

목록 보기

6/17

Hash

데이터를 다루는 기법 중 하나이다. 우리는 이미 해시라는 단어에 익숙하다. 인스타그램의 '해시태그' 기능 역시 해시 기법을 이용하여 게시물들을 구분하는 것이다.

아래처럼 #맛집 이라고 검색하게 되면, #맛집이라는 해시태그가 달려있는 게시물들이 한 뭉탱이로 묶여서 보여지게 된다. '#맛집' 이라는 데이터로 매핑된 게시물들이다.

Hash Function

데이터를 효율적으로 관리하기 위해 어떤 길이의 데이터든 하나로 고정된 길이의 데이터로 매핑하는 함수
매핑 전 원래 데이터를 Key, 매핑 된 후 데이터 값을 Hash Value 혹은 해시코드 라고 한다.
→ Key-Value 타입으로 매핑되는 과정 자체를 Hashing 이라고 함

Hash Table

Key-Value 쌍으로 이루어지는 데이터 구조다. 키와 배열의 인덱스를 이용하여 데이터를 저장하는 자료구조이다. HashTable 은 Hash Function 을 통해 Key 를 계산하여, 그 값을 배열의 인덱스로 사용한다. 이 때 Hash Function 에 의해 반환된 고유 값을 Hash Value 또는 Hash Code 라고 부른다.

때문에, 보통의 데이터 삽입이라 함은 아래와 같은 과정을 거친다.

삽입할 데이터의 Key 값을 Hash Function 에 대입

Hash Function 의 반환값 (해시 코드) 을 인덱스로 사용

해당하는 인덱스에 원하는 데이터 삽입

사람 이름을 Key 로 하고 해당 사람의 전화번호를 저장하는 전화번호부를 만든다고 가정해보자. 전체 데이터 크기가 10 이라고 한다면, John Smith 의 데이터를 저장할 때, 배열의 인덱스는 HashFuntion("John Smith") % 10 을 통해 인덱스 값을 계산하게 된다. 해당 예시에서는 해시코드 값으로 2가 나온 것이다.

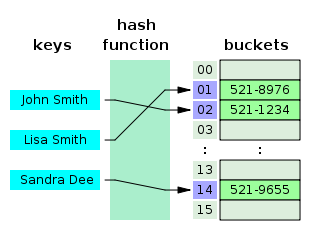
이런식으로 각각의 키 값에 대한 해시코드를 인덱스 삼아 데이터를 저장하게 되면, 데이터를 참조할 때에도 마찬가지로 HashFunction("John Smith") % 10 을 통해 해당 Key (여기서는 John Smith) 에 매핑되는 Value (전화번호) 를 얻을 수 있다. 결국 배열 형태의 자료구조에 인덱스 형태로 참조하는 것이기 때문에, 시간 복잡도가 O(1) 로 매우 우수하다.

하지만, HashFunction 의 설계 로직에 따라 계산된 해시코드 값, 즉 인덱스 값이 중복될 수 있다.

예를 들어 저장하고자 하는 Key 가 정수형이고 Hash Function 의 로직이 key % 10 이며 전체 사이즈가 10이라고 가정해보자. 이 경우 1, 11, 21 에 대한 해시코드 값이 모두 1 로 나오게 된다. 이 경우 해시 충돌 (Hash Collision) 이라고 한다.

아래 예시를 살펴보자. Sandra Dee 라는 사람의 전화번호를 저장하는 상황이다. Hash Function 에 의해 Sandra Dee 의 해시코드를 얻어본 결과 152 라는 Key 값이 나왔다. 따라서 152 를 통해 배열을 참조해보았는데, 이미 John Smith 라는 사람의 전화번호가 저장이 되어있는 것이다. 이 경우 어떻게 해야 할까?

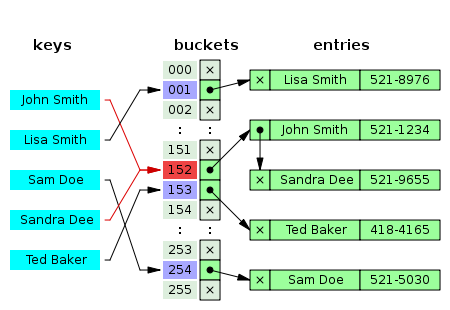
해시 충돌 상황을 해결할 수 있는 방안으로 여러 가지가 있다. 위 예제는 그 중 '체이닝 (Chaning)' 이라는 기법을 활용한 것이다. 기존 John Smith 의 데이터 뒤에 이어서 Sandra Dee 의 데이터를 저장한 것을 확인할 수 있다. 충돌 상황을 해결할 수 있는 방법 몇 가지를 알아보도록 하자.

Hash Collision Solution

1. 체이닝 (Chaining)

연결 리스트 (Linked List) 를 활용하는 것이다. 데이터를 삽입하다가 해시 충돌이 발생하면 연결 리스트로 데이터를 이어놓는 방식이다.

장점

연결 리스트만 사용하면 되기 때문에 복잡한 계산식이 필요 없음

해시 테이블이 채워질 수록 선형적으로 성능 저하 발생 (데이터 많은 경우 유리)

2. 개방 주소법 (Open Addressing)

체이닝 기법은 연결 리스트로 데이터를 이어놓을 뿐, 데이터의 주소값 (인덱스) 은 결국 바뀌지 않는 Closed Addressing 기법이다. 반면 개방 주소법은 해시 충돌이 일어나게 되면 비어있는 다른 인덱스를 찾아 데이터를 삽입하는 방식을 택한다. 이 때 다른 인덱스를 선택하는 로직으로는 대표적으로 3가지 로직 중 하나를 따른다.

선형 탐색 (Linear Probing)
→ 해시 충돌시 다음 인덱스, 혹은 몇 칸 뒤 인덱스에 데이터 삽입
제곱 탐색 (Quadratic Probing)
→ 해시 충돌시 제곱만큼 건너뛴 인덱스에 데이터 삽입
이중 해시 (Double Hasing)
→ 해시 충돌시 다른 해시 함수를 한 번 더 적용한 해시코드 이용

장점

체이닝 기법과 달리 포인터가 필요 없고, 때문에 포인터를 위한 추가적인 추가 공간도 필요 없음

데이터 삽입 및 삭제 시 오버헤드가 적은 편

저장할 데이터가 적을 때 유리한 전략

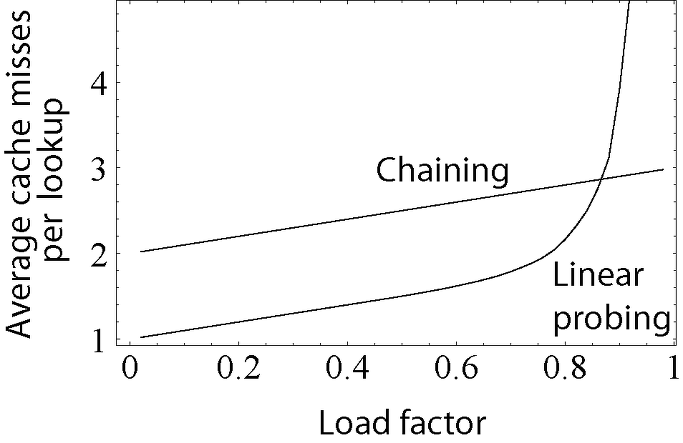
체이닝 vs 개방 주소법 성능 비교

체이닝은 선형적으로 성능이 저하되는 반면, 선형 탐색 로직을 채택한 개방 주소법의 경우 지수적으로 성능 저하가 발생하는 것을 알 수 있다. 어찌보면 데이터가 많아질수록 순차적으로 다른 인덱스를 참조하는 상황이 그만큼 빈번해지니 당연한 이야기이다. 따라서 데이터의 크기에 따라 전략적으로 선택하는 것이 좋다.

물론, 해시 함수를 잘 설계하여 충돌을 최소화하는 것이 가장 이상적이다.

Hash Table 장점과 단점 알아보기

장점

적은 리소스로 많은 데이터를 효율적으로 관리 가능
배열의 인덱싱 원리를 사용하기 때문에 탐색, 삽입, 삭제가 매우 빠름
Key ↔ Value 간에 연관성이 일절 없기 때문에 보안에도 많이 사용됨
데이터 캐싱에 많이 사용됨 (자주 Hit 하는 데이터를 O(1) 시간 복잡도로 얻어올 수 있음)

단점

Collision 발생 시 성능 저하가 발생함 + 공간 복잡도가 커질 수 있음
순서가 있는 데이터에는 적합하지 않음 (Key 는 순서와 무관하기 때문)
Hash Function 에 대한 의존도가 높음 (해시 함수 복잡해질 수록 성능 저하 우려)

번외) 자바에서의 HashTable 관련 Collection

자바 역시 Key-Value 타입으로 데이터를 저장하는 녀석들로 HashTable, HashTable 등이 있다. 이 둘의 차이는 동기화 지원 여부이다. 자바는 동기화 지원 여부를 차이점으로 두는 서로 비슷한 자료구조가 꽤 있는 편이다. 대표적으로 Vector 와 ArrayList 도 같은 맥락이다.