부동소수점에서 발생하는 오차

실수를 다룰 때, 계산 값에 오차가 생기는 경험을 해봤을 것이다.
이번에 실수 계산 로직을 다루면서 실수에 대해 자세히 알아보려한다.

실수 표현 방식

1. 고정 소수점(fixed point) 방식

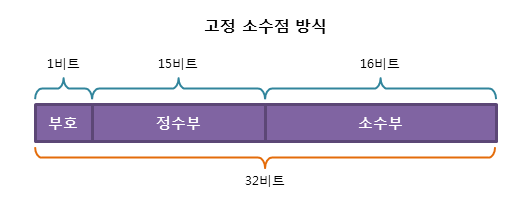
• 실수를 정수부와 소수부로 나누어 표현
• 소수부의 자릿수를 미리 정하여 고정된 자릿수의 소수를 표현하는 방식
• 구현하기 편리하지만, 표현 가능한 범위가 낮기에 소규모 시스템에서만 사용된다.

2. 부동 소수점(floating point) 방식

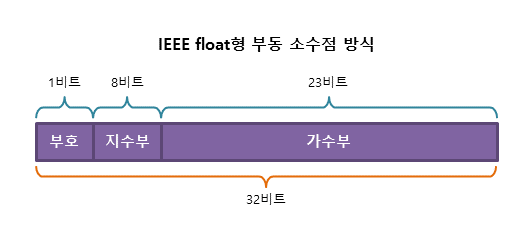
• 실수를 지수부와 가수부로 나누어 표현
• ±(1.가수부)×2지수부-127
  - 이 수식을 이용하여 넓은 범위의 실수를 표현할 수 있다.
  

부동 소수점 방식의 오차

• 고정 소수점 방식보다 더 넓은 범위의 실수를 표현할 수 있으나, 항상 오차가 존재한다.
• 실수는 무한한데 유한 개의 비트로 표현하기 위해서는 근삿값으로 표현할 수 밖에 없다.
  - 1/7(0.142857....) 은 결국 어디선가 반올림된 근삿값에 불과하고, 정확한 1/7라는 값을 표현할 수 없다.
  -> 실수 변수는 절대 정확한! 값을 갖고 있을 수 없다.(어느 정도의 정보 손신일 일어날 수 밖에 없다...)

예시

let a = 0.1;

for(let i = 0; i < 1000; i++) {
    a += 0.1;
}

console.log(a);	// 100.09999999999859

• 0.1을 1000번 더한 합계는 100이 되어야 하지만, 실제로는 100.09999999999859가 출력된다.

해결 방안

(JS에 국한된 이야기가 아님.)
1. float 보다는 double 자료형을 선택하자.

• double의 상대오차가 훨씬 작다
  - float: 10^-7 > double: 10^-15

2. 비교 연산을 할 때, 등호를 사용하면 안된다.

• 오차가 존재하기에 같은 값을 가져야 할지라도 실제는 다른 값일 때가 많다.
• abs(A-B) < EPS 을 통해 오차가 엡실론 보다 작을 경우, 같다고 판단

참고 자료

[CS] 부동 소수점 오차