정수론

소수 구하기

소수는 1과 자기 자신 외에 약수가 존재하지 않는 수를 말한다. 소수를 구하는 대표적인 판별법으로는 에라토스테네스의 체가 있다.

에라토스테네스의 체의 원리

에라토스테네스의 체의 원리를 이용하면 시간 복잡도는 최적화의 정도에 따라 다르겠지만, 일반적으로 O(nlog(logn)) 이다. 그 이유는 배수를 삭제하는 연산으로 실제 구현해서 바깥쪽 for문을 생략하는 경우가 빈번하게 발생하기 때문이다.
예를 들어, 2의 배수를 삭제한 후 3의 배수를 삭제하면 2의 배수이자 3의 배수인 6, 12, ... 등은 2의 배수를 삭제하는 연산에서 이미 삭제된 값이므로 3의 배수를 삭제하는 연산 시 삭제가 생략된다.

오일러 피

오일러 피 함수 P[n]의 정의는 1부터 n까지 범위에서 n과 서로소인 자연수의 개수를 뜻한다. 오일러 피의 개념을 알아야 관련 문제가 출제됐을 때 문제에 접근이 가능하기 때문에 간단히 집고 넘어가는게 좋다.

유클리드 호제법

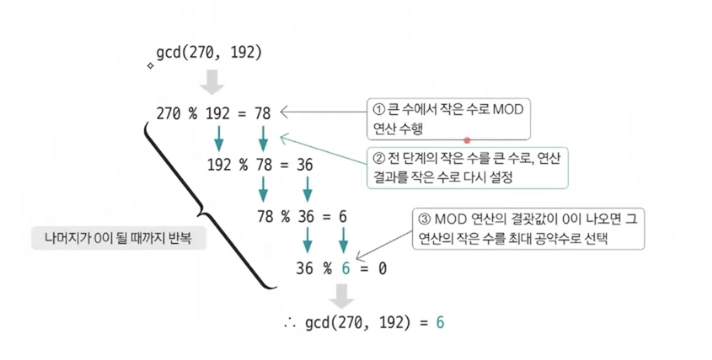
유클리드 호제법은 두 수의 최대 공약수를 구하는 알고리즘이다. 유클리드 호제법을 수행하려면 먼저 최대 공약수를 구하는데 사용하는 핵심 연산인 MOD 연산을 이해하고 있어야 한다.

MOD

유클리드 호제법 원리

실제 유클리드 호제법을 구현할 때는 재귀함수를 사용한다.

• 최대 공약수 구하기
  

• 최소 공배수 구하기
  최소 공배수는 a와 b가 주어졌을 때 a + b / 최대 공약수를 계산해서 구할 수 있다. 예를 들어, a = 36, b = 48일 때 a = 2 * 2 * 3 * 3이고 b = 2 * 2 * 3 * 4 이다. 여기서 최대 공약수 2 * 2 * 3으로 a + b를 나누면 중복으로 들어간 최대 공약수를 제외한 최소 공배수가 나오게 된다.

최소공배수 : 1934

문제

예제

나의 풀이

유클리드 호제법을 이용해서 두 수의 최대 공약수를 구하고 두 수를 곱한 값을 최대 공약수로 나누면 최소 공배수가 된다는 원리를 이용하는 문제이다.

# 최대 공약수 구하는 함수
def gcd(a, b):
    if b == 0:
        return a
    else:
        return gcd(b, a%b)
        
t = int(input())
for _ in range(t):
    a, b = map(int, input().split())
    c = gcd(a, b)
    print(a * b // c) # 정수로 결과값 리턴