[Algorithm] 탐색 + 그리디

HAHAHELLO·2025년 2월 1일

CS

목록 보기

6/14

탐색

깊이 우선 탐색 (DFS)

깊이 우선 탐색은 그래프 완전 탐색 기법 중 하나이다. 깊이 우선 탐색은 그래프의 시작 노드에서 출발하여 탐색할 한 쪽 분기를 정하여 최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동하여 다시 탐색을 수행하는 알고리즘이다.

깊이 우선 탐색 정리

깊이 우선 탐색은 실제 구현 시 재귀 함수를 이용하므로 스택 오버플로에 유의해야 한다. 깊이 우선 탐색을 응용하여 풀 수 있는 문제는 단절점 찾기, 단절선 찾기, 사이클 찾기, 위상 정렬 등이 있다.

스택 오버플로란 스택 메모리가 초과될 때 발생하는 오류를 말하며 주로 무한 재귀 호출, 깊은 재귀, 큰 지역 변수 사용 때문에 발생한다.

깊이 우선 탐색 과정

DFS는 한 번 방문한 노드를 다시 방문하면 안 되므로 노드 방문 여부를 체크할 배열이 필요하다. 탐색을 위해 스택을 사용한다.

DFS를 시작할 노드를 정한 후 사용할 자료구조 초기화하기
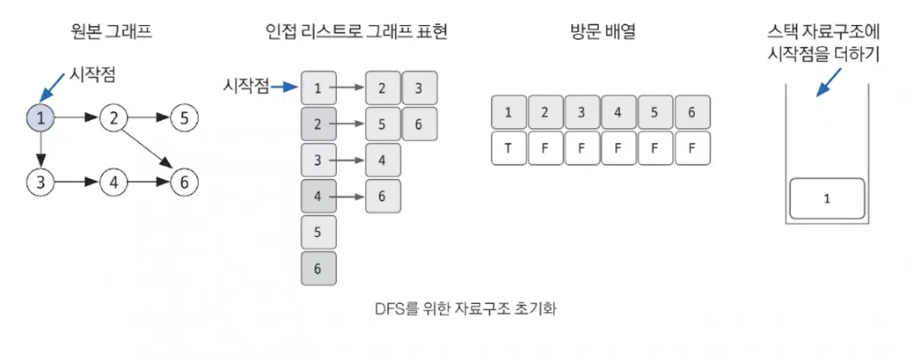
스택에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 스택에 삽입하기
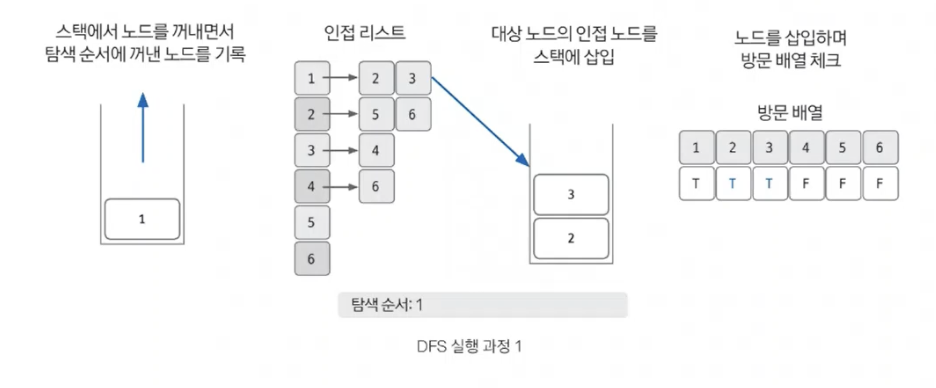
스택 자료구조에 값이 없을 때까지 반복하기
스택에 노드를 삽입할 때 방문 배열을 체크하고, 스택에서 노드를 뺄 때 탐색 순서에 기록하며 인접 노드를 방문 배열과 대조하여 살펴봐야 한다.

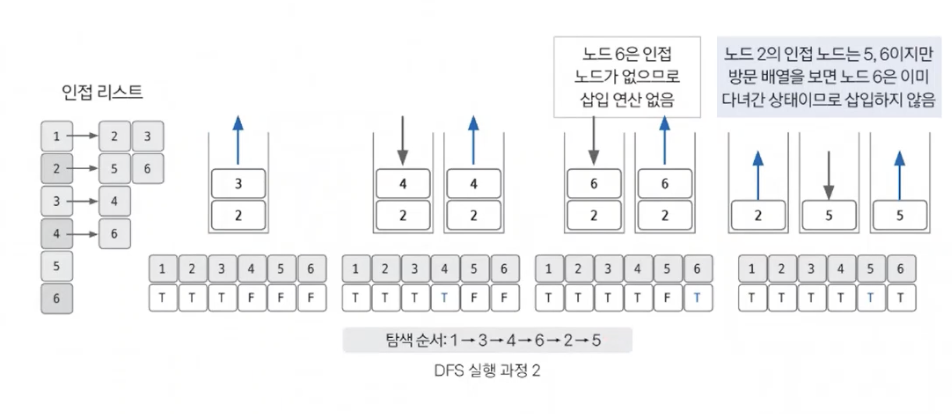
너비 우선 탐색 (BFS)

너비 우선 탐색도 그래프를 완전 탐색하는 방법 중 하나로, 시작 노드에서 출발해 시작 노드를 기준으로 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘이다.

너비 우선 탐색 정리

너비 우선 탐색 과정

BFS와 마찬가지로 방문했던 노드는 다시 방문하지 않으므로 방문한 노드를 체크하기 위한 배열이 필요하다. BFS와 차이점이 있다면 탐색을 위해 큐를 사용한다.

BFS를 시작할 노드를 정한 후 사용할 자료구조 초기화하기
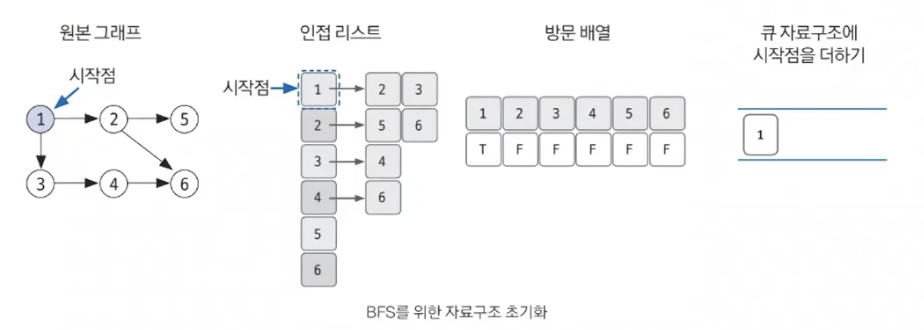
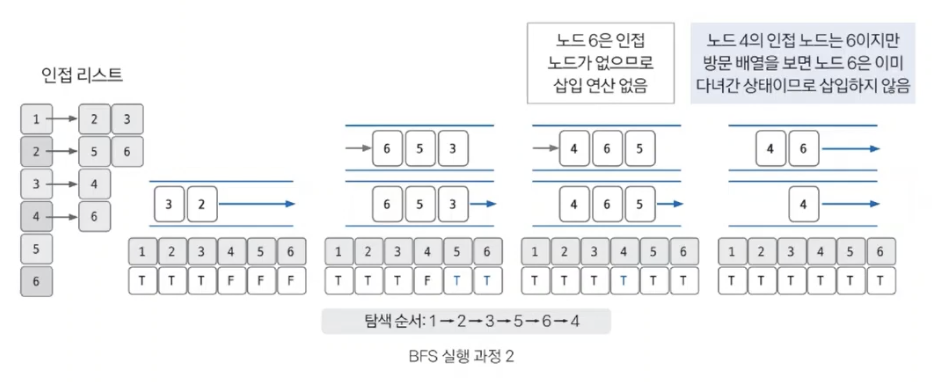
큐에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 큐에 삽입하기
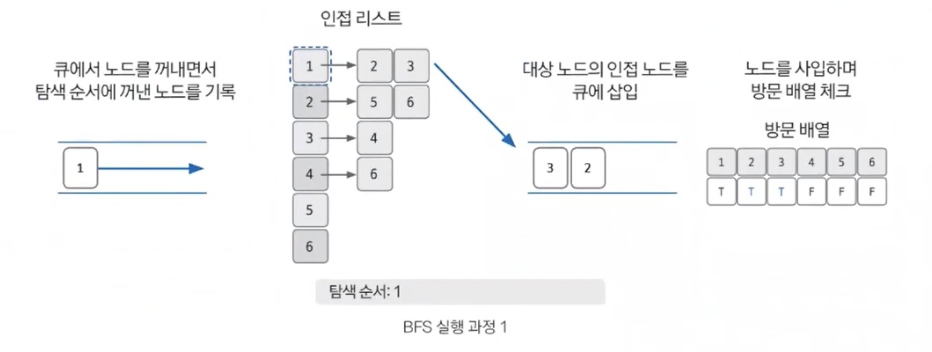
큐 자료구조에 값이 없을 때까지 반복하기

이진 탐색 (Binary Search)

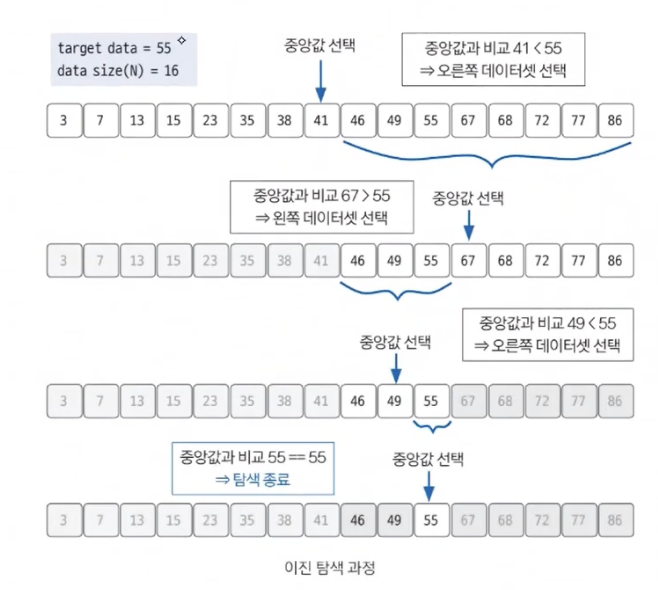
이진 탐색은 데이터가 정렬돼 있는 상태에서 원하는 값을 찾아내는 알고리즘이다. 대상 데이터의 중앙값과 찾고자 하는 값을 비교해 데이터의 크기를 절반씩 줄이면서 대상을 찾는다.

이진 탐색 정리

이진 탐색 과정

이진 탐색을 사용하면 n개의 데이터에서 logn번의 연산으로 원하는 데이터의 위치를 찾을 수 있다. 예를 들어 16개의 데이터면 최대 4번의 연산으로 원하는 데이터의 위치를 찾을 수 있다. 다만, 이진 탐색은 데이터가 정렬되어 있어야 한다.

탐욕법 (greedy)

탐욕법

그리디 알고리즘은 현재 상태에서 보는 선택지 중 최선의 선택지가 전체 선택 중 최선의 선택지라고 가정하는 알고리즘이다. 현재 상태에서 최선의 선택지를 선택했다고 해도 전체로 봤을 때는 최선의 선택이 아닐 가능성도 높다. 그래서 그리디 알고리즘으로 문제의 해법을 찾았을 때는 그 해법이 정당한지 검토해야 한다.

탐욕법 적용 가능한 조건

그리디 알고리즘을 사용할 수 있는 문제는 다음 두 가지 조건을 만족해야한다. 현재 선택이 이후의 선택에 영향을 주지 않으며, 최적의 해를 만들 수 있어야 하며, 문제의 전체 최적해가 부분 문제의 최적해로 구성될 수 있어야 한다.
예제로는 동전 거스름돈 문제(항상 가장 큰 단위의 동전을 선택하는 것이 최적의 해를 보장)와 다익스트라 알고리즘(현재까지 최단 경로가 전체 최단 경로에도 기여)가 있다.

동전 거스름돈 문제: 거스름돈을 줄 때 동전 개수를 최소화하려면? (단, 동전 단위가 500원, 100원, 50원, 10원일 때)

def min_coin_count(n, coins):
    coins.sort(reverse=True)  # 가장 큰 단위부터 정렬
    count = 0
    for coin in coins:
        count += n // coin
        n %= coin
    return count

print(min_coin_count(1260, [500, 100, 50, 10]))  # 6

활동 선택 문제: 여러 개의 회의 일정이 주어질 때, 최대한 많은 회의를 배치하는 방법은?

def max_meetings(meetings):
    meetings.sort(key=lambda x: x[1])  # 종료 시간이 빠른 순으로 정렬
    count, end_time = 0, 0
    for start, end in meetings:
        if start >= end_time:  # 새로운 회의를 추가할 수 있는 경우
            count += 1
            end_time = end
    return count

meetings = [(1, 3), (2, 5), (3, 9), (6, 8), (8, 9)]
print(max_meetings(meetings))  # 3