조합과 순열
조합은 n개의 숫자에서 r개를 뽑는 경우의 수를 뜻한다. 조합과 비교되는 순열은 n개의 숫자 중 r개를 뽑는 순서를 고려해 나열한 경우의 수를 이야기 한다. 즉, 조합에서는 데이터 1, 2, 3과 3, 2, 1을 같은 경우로 판단하고, 순열은 다른 경우로 판단한다.
알고리즘으로 조합 이해하기
-
특정 문제를 가정하기
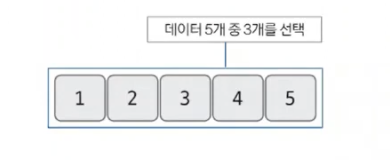
-
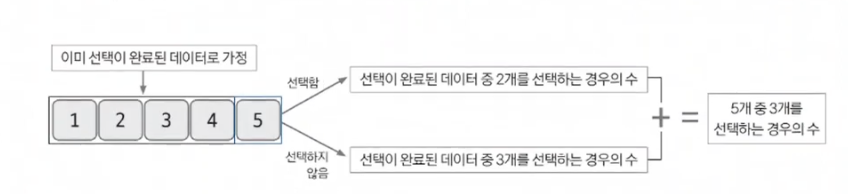
모든 부분 문제가 해결된 상황이라고 가정하고 지금 문제 생각하기
마지막 번호를 뽑지 않는다고 가정했을 때, 5개 중에 3개를 뽑는 경우의 수는 4개에서 3개를 뽑는 경우의 수와 같다. 마지막 번호를 뽑는 다면, 1개는 이미 뽑혀 있기 때문에 4개에서 2개를 뽑는 경우의 수와 같다.
-
특정 문제를 해결한 내용을 바탕으로 일반 점화식 도출하기
D[i][j] = D[i-1][j] + D[i-1][j-1]조합 파이썬으로 구현하기
반복문으로 구하기
arr = ['A', 'B', 'C']
N = len(arr)
my_comb = []
for i in range(N - 1):
for j in range(i + 1, N):
my_comb.append((arr[i], arr[j]))
print(my_comb) # [('A', 'B'), ('A', 'C'), ('B', 'C')]조합 내장 함수로 구하기
기본형은 combinations(리스트, 조합수)이며 내장 함수를 사용하기 위해서는 from itertools import combinations로 함수를 import 해야한다.
from itertools import combinations
arr = ['A', 'B', 'C']
print(list(combinations(arr, 2))) # [('A', 'B'), ('A', 'C'), ('B', 'C')]순열 파이썬으로 구현하기
반복문으로 구하기
arr = ['A', 'B', 'C']
N = len(arr)
my_permu = []
for i in range(N):
for j in range(N):
if i == j:
continue
my_permu.append((arr[i], arr[j]))
print(my_permu)
# [('A', 'B'), ('A', 'C'), ('B', 'A'),
# ('B', 'C'), ('C', 'A'), ('C', 'B')]순열 내장 함수로 구하기
기본형은 permutations(리스트, 조합수)이며 내장 함수를 사용하기 위해서는 from itertools import permutations로 함수를 import 해야한다.
from itertools import permutations
arr = ['A', 'B', 'C']
print(list(permutations(arr, 2)))
# [('A', 'B'), ('A', 'C'), ('B', 'A'),
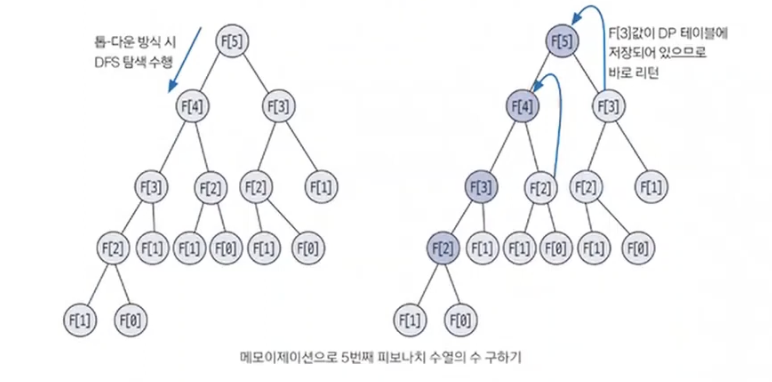
# ('B', 'C'), ('C', 'A'), ('C', 'B')]동적 계획법
동적 계획법은 Dynamic Program 혹은 DP라고도 부른다. 동적 계획법은 복잡한 문제를 여러 개의 간단한 문제로 분리하여 부분의 문제들을 해결함으로써 최종적으로 복잡한 문제의 답을 구하는 방법을 뜻한다.
동적 계획법 이해하기
피보나치 수열 점화식
D[i] = D[i-1] + D[i-2]메모이제이션 원리
메모이제이션은 부분 문제를 풀었을 때 이 문제를 DP 테이블에 저장해 놓고 다음에 같은 문제가 나왔을 때 재계산하지 않고 DP 테이블의 값을 이용하는 것을 말한다.