트리
트리는 노드와 에지로 연결된 그래프의 특수한 형태이다.
트리의 특징
- 순환 구조를 지니고 있지 않고, 1개의 루트 노드가 존재한다.
- 루트 노드를 제외한 노드는 단 1개의 부모 노드를 갖는다.
- 트리의 부분 트리 역시 트리의 모든 특징을 따른다.
- 트리에서 임의의 두 노드를 이어주는 경로는 유일하다.
트리의 구성 요소
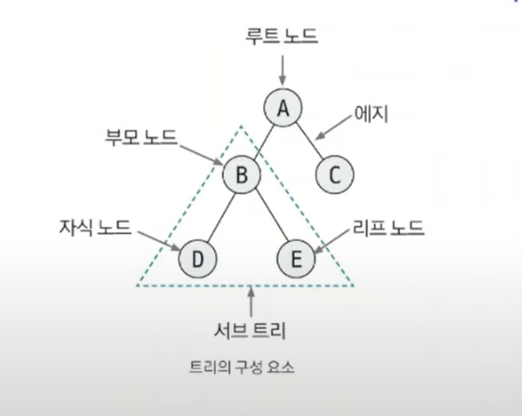
노드: 데이터의 index와 value를 표현하는 요소에지: 노드와 노드의 연결 관계를 나타내는 선루트 노드: 트리에서 가장 상위에 존재하는 노드부모 노드: 두 노드 사이의 관계에서 상위 노드에 해당하는 노드자식 노드: 두 노드 사이의 관계에서 하위 노드에 해당하는 노드리프 노드: 트리에서 가장 하위에 존재하는 노드(자식 노드가 없는 노드)서브 트리: 전체 트리에 속한 작은 트리
이진 트리
이진 트리는 각 노드의 자식 노드(차수)의 개수가 2 이하로 구성된 트리를 말한다.
이진 트리의 종류
일반적으로 코딩 테스트에서 데이터를 트리에 담는다고 하면 완전 이진 트리 형태이다.
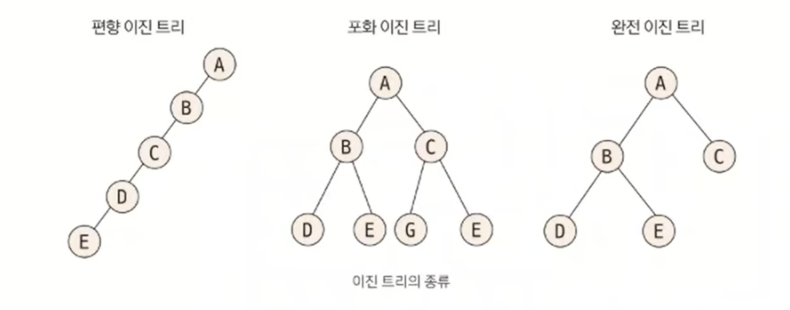
편향 이진 트리: 노드들이 한쪽으로 편향돼 생성된 이진 트리포화 이진 트리: 트리의 높이가 모두 일정하며 리프 노드가 꽉 찬 이진 트리완전 이진 트리: 마지막 레벨을 제외하고 완전하게 노드들이 채워져 있고, 마지막 레벨은 왼쪽부터 채워진 트리이다.
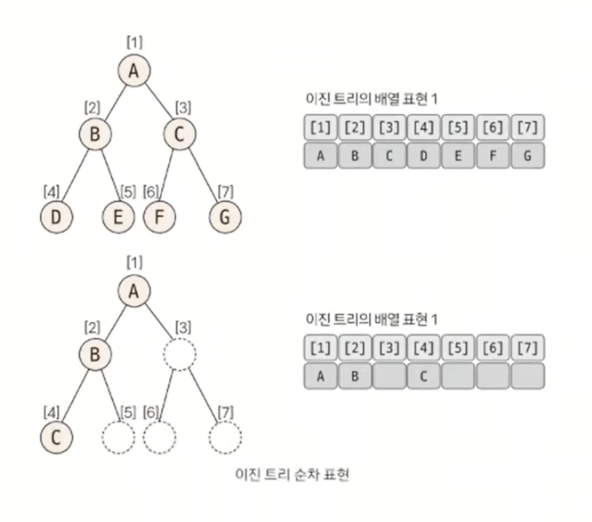
⭐️이진 트리의 순차 표현
가장 직관적이면서 편리한 트리 자료구조 형태는 배열이다. 코딩 테스트에서 트리 문제가 나오면 아래의 방식으로 데이터를 담는게 일반적이다.
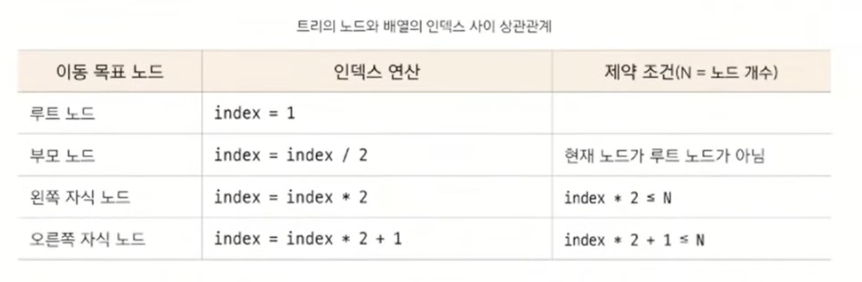
⭐️세그먼트 트리(인덱스 트리)
세그먼트 트리는 주어진 데이터의 구간 합과 데이터 업데이트를 빠르게 수행하기 위해 고안해낸 자료구조의 형태이다. 더 큰 범위는 인덱스 트리라고 불리는데, 코딩 테스트 영역에서는 큰 차이가 없다.
세그먼트 트리의 과정
- 트리 초기화하기
리프 노드의 개수가 데이터의 개수(N) 이상이 되도록 트리 배열을 만든다. 트리 배열의 크기를 구하는 방법은2ᴷ>=N을 만족하는k의 최솟값을 구한 후2ᴷ*2를 트리 배열의 크기로 정의하면 된다. 리프 노드의 시작 위치를 트리 배열의 인덱스로 구해야 하는데, 구하는 방식은2ᴷ를 시작 인덱스로 하면 된다.
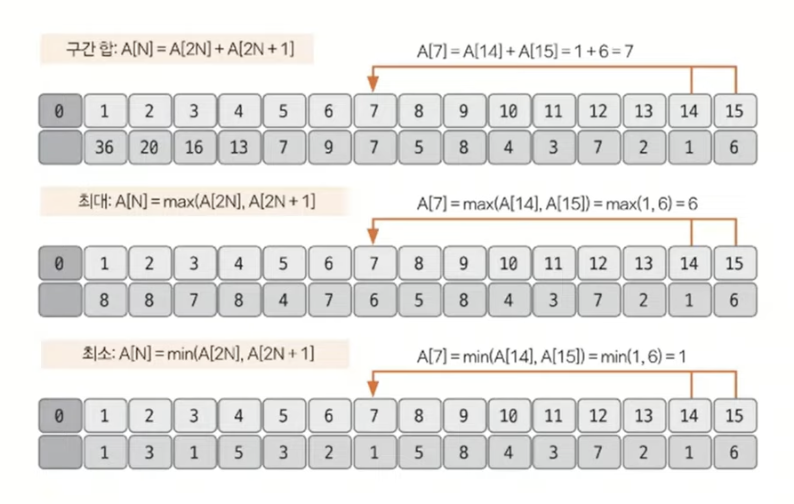
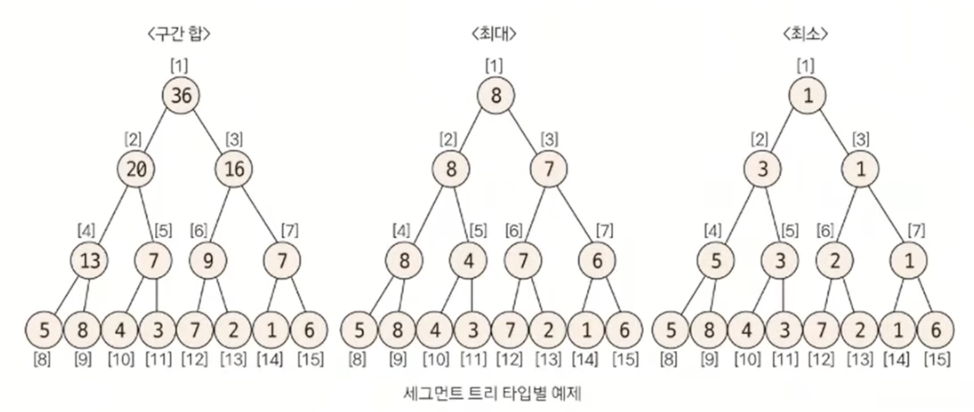
- 질의값 구하기
주어진 질의 인덱스를 세그먼트 트리의 리프 노드에 해당하는 인덱스로 변경한다. 방법은세그먼트 트리 index = 주어진 질의 index + 2ᴷ - 1이다.



end_index < start_index가 되면 종료하고 값을 구한다. 2~6번 구간 합의 값은 선택된 노드의 합인 8 + 9 + 7 = 24가 된다.
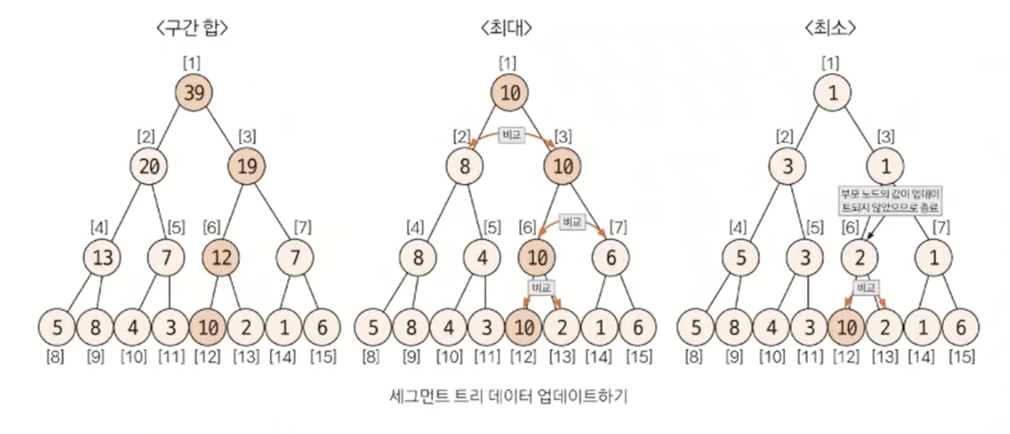
- 데이터 업데이트하기
업데이트 방식은 자신의 부모 노드로 이동하면서 업데이트한다는 것은 동일하지만, 어떤 값으로 업데이트할 것인지에 관해서는 트리 타입별로 다르다.
최소 공통 조상(LCA)
최소 공통 조상(LCA)은 트리 그래프에서 임의의 두 노드를 선택했을 때 두 노드가 각각 자신을 포함해 거슬러 올라가면서 부모 노드를 탐색할 때 처음 공통으로 만나게 되는 부모 노드를 말한다.
일반적인 최소 공통 조상 구하기
- 트리의 높이가 크지 않을 때
먼저 루트 노드에서 탐색을 시작해 각 노드의 부모 노드의 깊이를 저장한다.
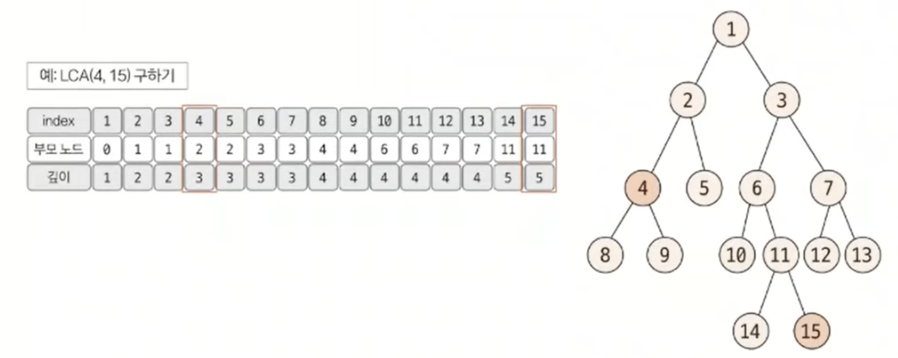
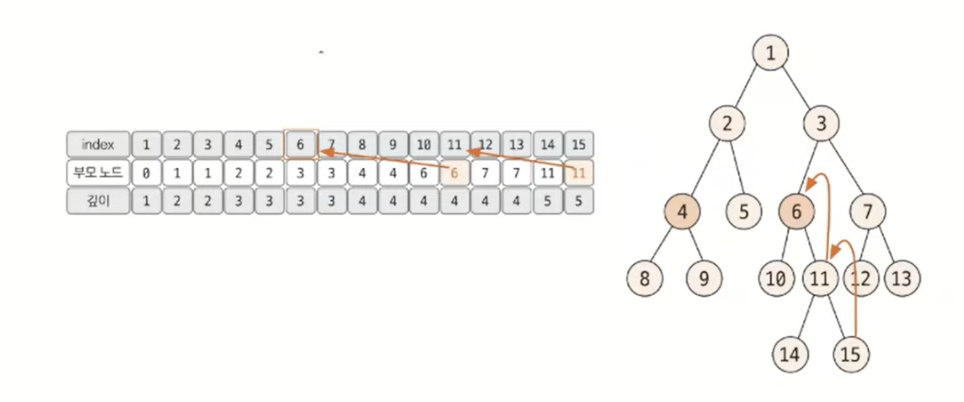
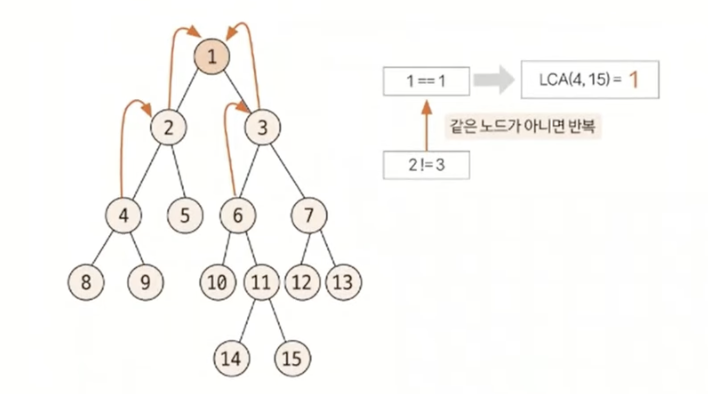
최소 공통 조상 빠르게 구하기
최고 공통 조상 빠르게 구하기의 핵심은 서로의 깊이를 맞춰 주거나 같아지는 노드를 찾을 때 기존에 한 단계씩 올려 주는 방식에서 2ᴷ씩 올라가 비교하는 방식이다. 따라서 기존에 자신의 부모 노드만 저장해 놓던 방식에서 2ᴷ번째 위치의 부모 노드까지 저장해 둬야 한다.
- 부모 노드 저장 배열 만들기
부모 노드의 배열의 정리
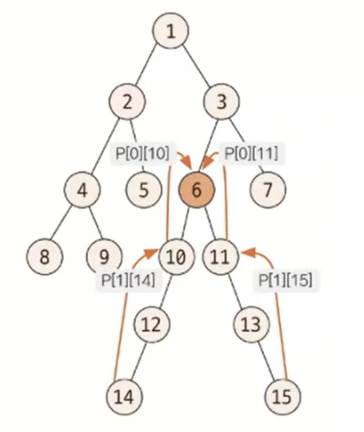
P[K][N] = N번 노드의 2ᴷ번의 부모의 노드 번호 부모 노드 배열의 점화식
점화식에서 N의 2ᴷ번째 부모 노드는 N의 2ᴷ⁻¹번째 부모 노드의 2ᴷ⁻¹번째 부모 노드라는 의미이다. 예를 들어 K = 4라고 가정하면 N의 16번째 부모 노드는 N의 여덟 번째 부모 노드의 여덟 번째 부모 노드라는 의미이다.
P[K][N] = P[K -1][P[K - 1][N]]
- 선택된 두 노드의 깊이 맞추기
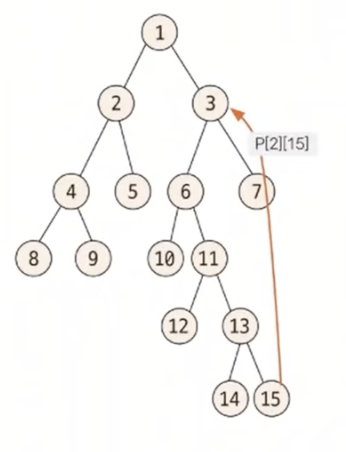
- 최소 공통 조상 찾기
K값을 1씩 감소하면서 P배열을 이용해 최초로 두 노드의 부모가 달라지는 값을 찾는다. 최초로 달라진ㄴ K에 대한 두 노드의 부모 노드를 찾아 이동한다. 이를 K가 0이 될 때까지 반복하나다. 반복문이 종료된 후 이동한 2개의 노드가 같은 노드라면 해당 노드가, 다른 노드라면 바로 위의 부모 노드가 최소 공통 조상이 된다.