PR: Quantum Neural Architecture Search

This article is a review about paper Quantum circuit architecture search for variational quantum algorithms, publised at npj Quantum Inf. in 2022 May.

1. Introduction

Variational quantum algorithms(VQAs) are widely utilized to seek quantum advantages on NISQ devices, but some problems of variational quantum algorithms have been revealed. Trainability and robustness of quantum circuits are in a trade off relationship: barren plateau and accumulated noise hinders training of high-depth quantum circuits while shallow circuits lacks expressivity and robustness. Thus it is important to maximally improve the robustness and trainability but optimal architecture of the variational quantum circuit was task- and data-dependent, highly varying across different settings. Therefore, authors presented a resource and runtime efficient scheme called quantum architecture search(QAS) which automatically seeks a near-optimal circuit architecture to balance benefits and side-effects by adding more quantum gates to achieve a good performance.

2. Method

VQA continuously updates parameter of an ansatz $U(\theta)$ to find the optimal $\theta$ that minimizes the value of objective function. VQA can be formulated with input $\mathcal{Z}$ and objective function $\mathcal{L}$, i.e. $\theta^* = \arg\min_{\theta}\mathcal{L}(\theta,\mathcal{Z})$. Architecture search space was constained under supernet, which indicates the generic structure of variational quantum circuit consists of basic building blocks. Authors suggested a variational circuit architecture which can be decomposed into products of circuits.

$U(\theta) = \prod_{l=1}^L U_l(\theta) \in SU(2^N)$

Quantum architecture search, QAS aims at noise inhibition and trainability enhancement of searched ansatz from ansatz pool. The size of ansatz pool $|S|$ is determined by the number of qubits N, the maximum circuit depth L, and the number of allowed types of
quantum gates Q, i.e. $|S|=\mathcal{O}(Q^{NL})$.

Objective of the suggested QAS algorithm can be written as $(\theta^*,a^*) = \arg\min_{\theta, a \in \mathcal{S}} \mathcal{L}(\theta, a, \mathcal{Z}, \epsilon_a)$, where $a$ is an ansatz indicator variable and $\epsilon_a$ represents quantum system noise induced by ansatz $U_a(\theta)$. Suggested objective forces to learn optimal parameter of optimal architecture determined by $a$ aware of trainability and noise effect. Due to the complex landscape of objective function over parameter and architecture space, they suggested one-stage optimization strategy that overcomes the weakness of two-stage optimization strategy which is widely utilized at previous works. Two-stage optimization strategy, individual optimization all possible ansatzes followed by ranking is computationally expensive: classical optimizer should store $\mathcal{O}(\mathcal|{S}|\cdot Q^{NL})$ parameters. However, QAS leverages the advantage of weight sharing to efficiently search over the ansatz architecture space specified by supernet. Suggested one-stage optimization strategy can be depicted as following pseudocode.

In order to assess the effectiveness of suggested QAS algorithm, benchmark VQA ansatz and QAS algorithm are both applied for classification task and ground state energy estimation of hydrogen molecule. Quantum kernel classifer with objective function $\mathcal{L} \gets MSE(\hat{y}, y)$ was utilized for binary classification of simulated dataset, while ground state energy of the hydrogen molecule was estimated by variational quantum eigensolver(VQE) with corresponding hamiltonian $H_h = g+\sum_{i=0}^3 g_iZ_i + \sum_{i=1, k=1, i<k}^3g_{i,k}Z_iZ_k+g_aY_0X_1X_2Y_3+g_bY_0Y_1X_2X_3+g_cX_0X_1Y_2Y_3+g_dX_0Y_1Y_2X_3 (g\textit{ are known scalars})$.

3. Results

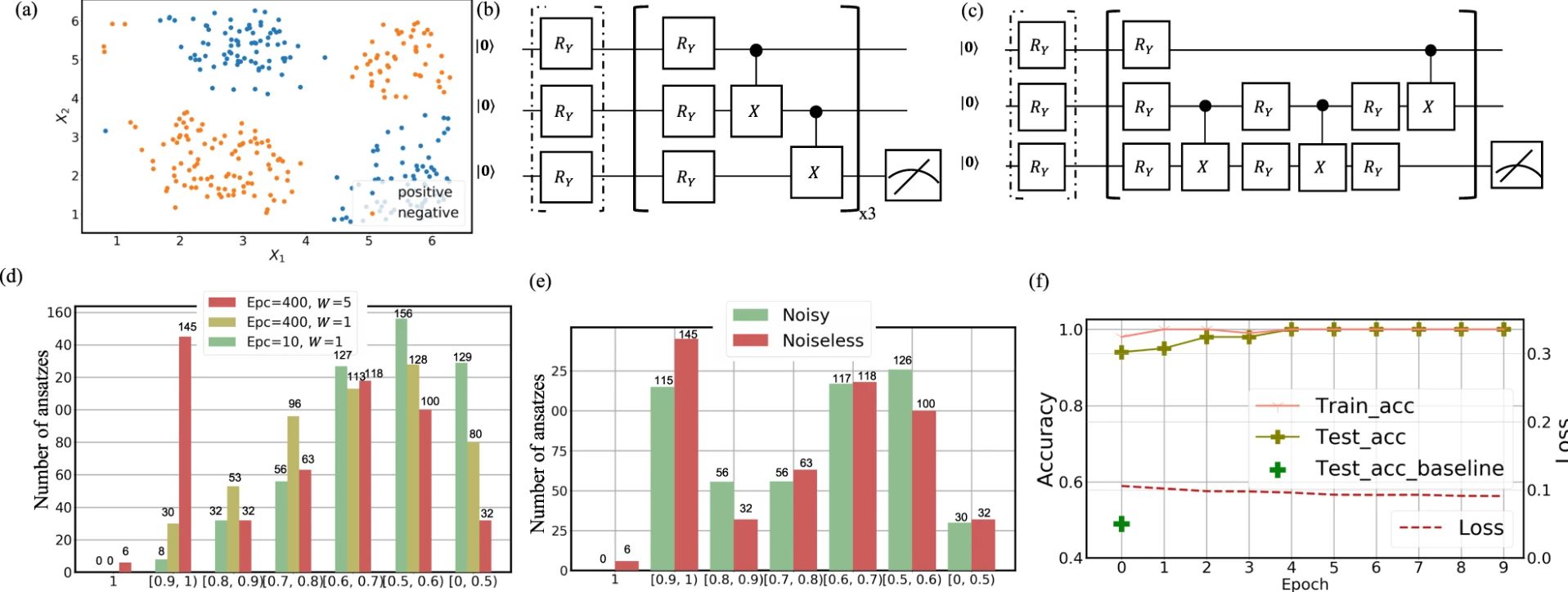
Figures below depict the simulation results for the classification of in silico dataset and ground state energy estimation of hydrogen molecule. Distribution of simulated classification dataset is visualized at Figure 1-(a). For comparison, benchmark ansatz of Figure 1-(b) was utilized as a counterpart of QAS algorithm. Under noisy setting, QAS algorithm was applied and ansatz evolution reached to the final circuit architecture depicted in Figure 1-(c). For hyperparameters, evolution time T and number of supernet W can be modified especially when QAS algorithm is parallelized. During evolution, QAS algorithm had higher chance of searching ansatz with higher accuracy as evolution time increases and number of suggested supernet increases. Figure 1-(d) and 1-(e) shows the evolutionary landscape of searched ansatz architecture based on test accuracy. Quantitative accuracy after selecting final ansatz is presented at Figure 1-(f), while test accuracy of QAS algorithm excels the counterpart of baseline ansatz.

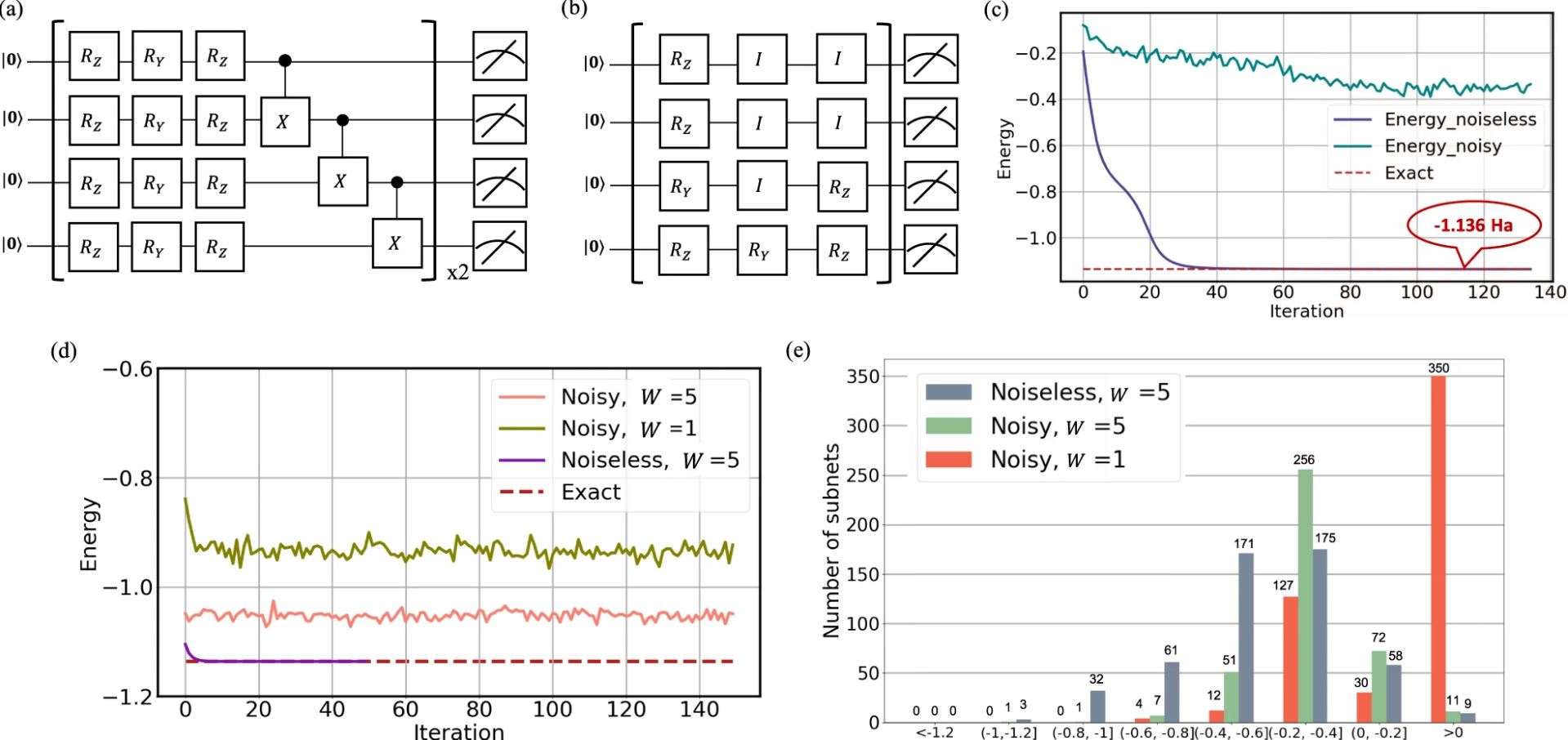
Figures below depict the simulation results for ground state energy estimation of hydrogen molecule, which is known as -1.136Ha. Figure 2-(a), 2-(b) corresponds to conventional VQE ansatz and searched ansatz architecture from QAS algorithm. According to the quantitative results from Figure 2-(c)~(e), suggested ansatz showed high accuracy on estimating ground state energy of the hydrogen molecule under noisyless condition while showed inconsistency under noisy settings.

4. Own discussion

Paper "Quantum circuit architecture search for variational quantum algorithms" suggested the first quantum analog of neural architecture search, which was known as common strategy for optimizing neural network architecture targeting various tasks. QAS, the suggested quantum circuit architecture search algorithm can search for near-optimal architecture of variational circuit by constraining the architecture search space under SuperNet. Authors verified that QAS algorithm on quantum kernel classifier and variational quantum eigensolver circuits was able to suggest near-optimal architecture for simulated data classification and ground state energy estimation of hydrogen molecule. However, there is a room for improvement targeting quantum circuit architecture search: conventional bayesian optimization and reinforcement learning based neural architecture search algorithms also have an opportunity at searching quantum circuit architectures, while sophisticated design of SuperNet which resembles QCNN also can provide a powerful prior at searching better architectures. This paper is especially interesting for me, for following two reasons.

• SuperNet design
  Suggested supernet architecture, which consists of fixed structure of building blocks restricts the architecture design space with a powerful prior assumption. Each building blocks have identical structure: for 2 qubits, each qubits are undergoing one of the following operations ${R_X, R_Y, R_Z}$ parameterized by $\theta$ which is followed by conditional gates. Recently, QCNN have been suggested as an efficient and effective ansatz design for classification, leveraging the power of weight sharing and pooling operation which is analogous to clasical CNN. Thus it is questionable that utilizing the backbone architecture of QCNN is a better prior assumption, compared to the supernet architecture which authors have suggested in this paper.

• Optimization strategy
  Authors have mentioned that optimization of QAS objective function is challenging, thus suggested a one-stage strategy that selects optimal ansatz architecture followed by parameter optimization of selected ansatz. While ranking strategy is one of the naive approach, classical neural architecture search algorithms adopt learnable parameters to configure the architecture of neural network. Reinforcement-learning based optimization has a chance to work as a powerful black-box approach for exploring through complex landscape of suggested objective function.