백트래킹 알고리즘이란,
백트래킹 알고리즘은 코딩테스트에서 출제빈도가 높은 알고리즘 중 하나로, 특정 그래프에서 완전 탐색이 가능한 알고리즘이다. 특히 모든 경우의 수를 고려해야할 때 유용하다.
일반적으로 그래프/트리의 모든 원소를 완전 탐색하기 위한 목적으로 사용할 수 있다.
백트래킹 VS DFS
- DFS : 일반적으로 완전 탐색 목적으로, 재귀 함수를 이용해 구현한다.
- 백트래킹 : 백트래킹도 재귀 함수를 이용해 구현하는 것이 일반적이지만, 단순히 완전 탐색하는 것이 아니라 조건에 따라 유망한 노드로 이동한다.
→ DFS에 비해 백트래킹이 코딩테스트 출제 빈도가 더 높다.
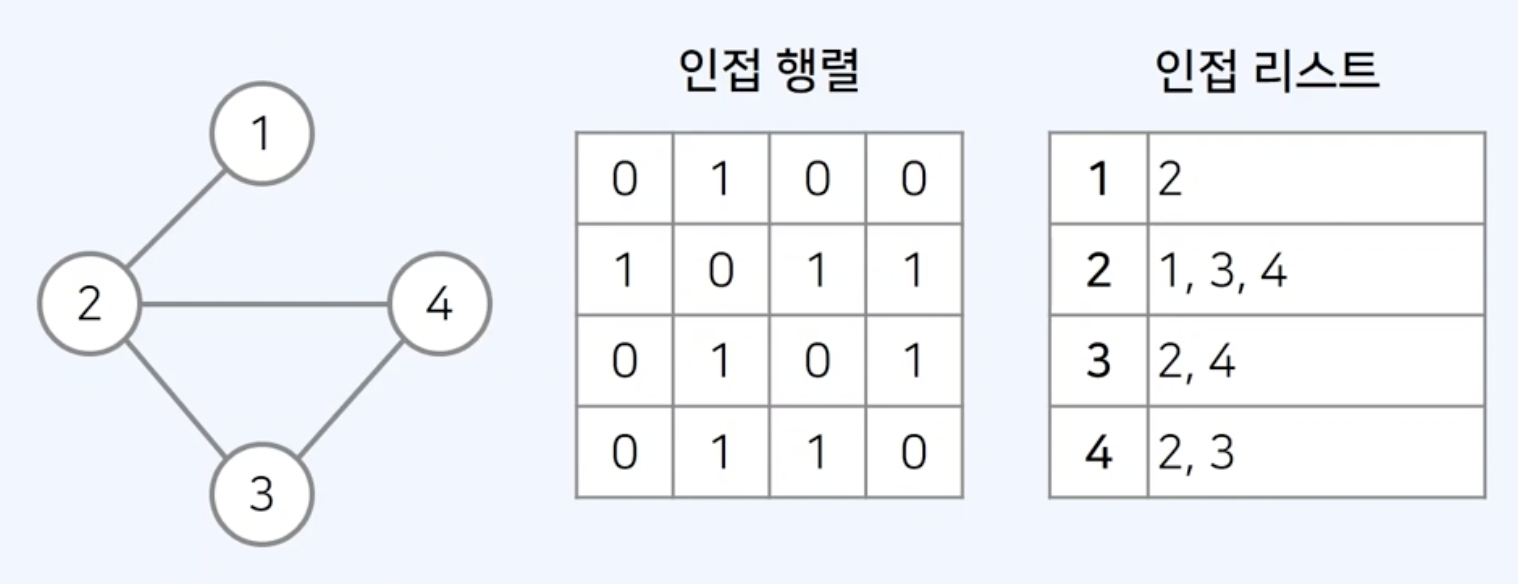
그래프 표현 방식
그래프를 표현하는 방식은 2가지로 나뉜다.
- 인접 행렬
- 인접 리스트
♟️ 백트래킹 대표 문제 : N-Queen 문제
N x N 체크 보드 위에 퀸 N 개가 서로 공격할 수 없게 놓는 문제이다.
- 예로 8 x 8에 하나의 퀸이 놓여 있는 예시로, 아래 보드에서 하얀색 칸에만 다른 퀸을 올려놓을 수 있다.
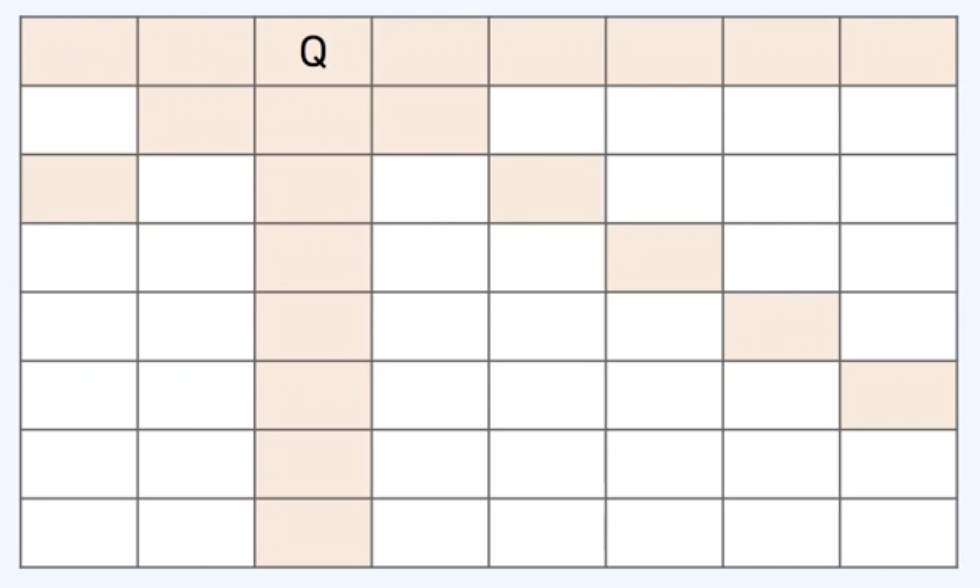
- 따라서 8 x 8 보드에서 퀸을 서로 공격할 수 없게 놓는 예시는 다음과 같으며, 해당 경우의 수를 구하는 알고리즘이 바로 백트래킹 알고리즘이다.
퀸을 놓는 규칙
- 퀸은 각 행(가로)마다 1개씩만 존재해야 한다.
- 기존 퀸의 상하좌우 + 대각선이 아닌 위치에 놓아야 한다.
→ 이는 트리 구조로 표현할 수 있다.
백트래킹을 진행할 때, 경우의 수를 최대한으로 줄이는 방법은?
이전까지 놓았던 퀸들과 상충되지 않는 조건을 만족하는 위치에 대해서만 재귀함수를 호출한다.
1) 완전 탐색 : 재귀함수를 통해 모든 경우의 수를 다 찾은 뒤에, 각 경우마다 가능한지 검사하는 방법
2) 백트래킹 : 유망한 경우에 대해서만 재귀함수를 호출하는 방법
→ 즉, 불가한 경우의 수를 우선적으로 제거하는 백트래킹 방법이 훨씬 시간복잡도가 낮고, 더 효율적이다.
백트래킹의 기본 형태
function recursive() {
if (종료 조건을 만족하면) {
처리
}
for (자식 노드를 하나씩 확인하며) {
if (잉의의 조건을 만족하면)
자식 노드 방문 처리;
재귀 함수 호출;
자식 노드 방문 처리 해제;
}
}
}
N-Queen 문제 해결 아이디어
- 백트래킹을 이용해 완전 탐색을 하더라도
유망한 경우에 대해서만 탐색을 진행해 경우의 수를 훨씬 줄일 수 있다.
따라서 가능한 노드에 대해 계속해서 재귀적으로 함수를 호출한다.
가능한 노드인지 여부는 다음 두가지 조건을 확인한다.
1. 같은 행에 존재하는지
2. 대각선에 존재하는지
N-Queen 풀이
// 전체 맵의 크기
let n = 8;
// 현재 체스판에 놓인 퀸의 위치 정보들로, (x, y)형태의 2차원 배열 형태
let queens = [];
// (x, y) 위치에 퀸을 놓을 수 있는지 확인하는 함수 (조건에 따라 완전 탐색을 수행)
function possible(x, y) {
// 현재까지 놓았던 모든 퀸의 위치를 하나씩 확인한다.
for (let [a, b] of queens) {
// 1. 행이나 열이 같다면 놓을 수 없다.
if (a === x || b === y) return false;
// 2. 대각선에 위치한 경우 높을 수 없다.
if (Math.abs(a - x) === Math.abs(b - y)) return false;
}
// 두 경우에 해당하지 않은 경우 -> 가능
return true;
}
let cnt = 0;
// 첫번째 행부터 퀸을 놓는 함수
function dfs(row) {
// 퀸을 n개 배치할 수 있는 경우를 count한다.
if (row === n) cnt++;
// 현재 행(row)에 존재하는 열을 하나씩 확인한다.
for (let i = 0; i < n; i++) {
// 1. 만약 현재 위치에 놓을 수 없다면 무시하고,
if (!possible(row, i)) continue;
// 2. 가능하다면 현재 위치에 퀸을 놓고,
queens.push([row, i]);
// 재귀 함수를 호출한다.
dfs(row + 1);;
// 확인한 현재위치의 퀸은 제거한다.
queens.pop();
}
}
dfs(0);
console.log(cnt);