
탐욕 알고리즘(Greedy Algorithm)이란 ?
흔히 그리디 알고리즘, 또는 탐욕법이라고 부른다.
현재 상황에서 당장 가장 좋아보이는 상황만을 선택하는 알고리즘 방법으로, 최적의 해를 구하기 위한 근사적인 방법으로 사용될 때가 많다.
➕ 탐욕 알고리즘은 코딩테스트에서 자주 등장하는 알고리즘 중 하나이다.
탐욕 알고리즘 vs 완전 탐색
루트에서 출발해 단말 노드까지 도착할때, 거쳐가는 노드의 합이 가장 큰 경우를 산출해라.
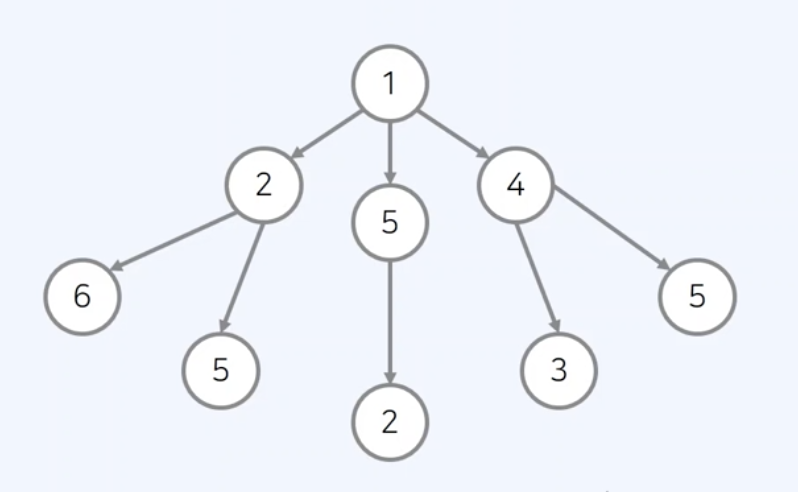
완전 탐색
완전 탐색은 전체 노드를 탐색해 루트에서 출발해 단말 노드까지 가는 경우, 노드의 합이 가장 큰 경우를 도출한다.
그래서 도출한 값은 1 -> 4 -> 5로 최적의 해는 10이다.
탐욕 알고리즘
루트에서 출발해 당장 값이 높은 수의 노드로 향하기 때문에 1 -> 5 -> 2 경로로 최적의 해로 8을 구하게 된다.
탐욕 알고리즘 장/단점
- 최적의 해를 놓칠 수 있다.
- 하지만 최적의 해가 아닌, 근사해를 구하는 목적이라면 최적의 알고리즘 방법이다.
✏️ 결론
- 탐욕 알고리즘은 최적의 해를 보장하진 못하지만, 모든 경우를 탐색하지 않아도 되기 때문에 완전 탐색과 비교해 시간 복잡도 상 효율이 높다.
- 즉 탐욕 알고리즘은 시간 복잡도를 절약하고 정확한 답이 아닌 근사해를 구할 때 사용하기 좋은 알고리즘이다.
💡 코딩 테스트에서의 탐욕 알고리즘
- 일반적인 채점 시스템은 참가자의 코드 결과가 정해진 결과와 같은지 확인한다.
- 따라서, 일반적으로 탐욕 방법으로 최적의 해가 보장되는 문제가 출제된다.
탐욕 알고리즘 알아보기
탐욕 알고리즘의 접근 방법
- 방법 고안하기 : 현재 상황에서 어떤 것을 선택할지 알고리즘을 고안한다.
- 정당성 확인하기(증명 단계) : 자신이 고안한 알고리즘이 항상 최적의 해를 보장하는지 확인한다.
✏️ 탐욕 알고리즘 예시: 거스름 돈 문제
거스름 돈 문제는 전형적인 탐욕 알고리즘 예시 문제이다.
Q. 손님에게 6,480원을 거슬러 주어야 할때, 동전 개수의 최솟값은?
(단 이때 동전 단위는 500원, 100원, 50원, 10원이다.)
S. 문제 풀이 방법
가장 큰 화페부터 거슬러준다.
500원 최대 -> 100원 최대 -> 50원 최대 -> 10원
-> 12 + 4 + 1 + 3개
A. 총 20개
거스름 돈 문제의 해법의 정당성 분석
Q. 단순히 큰 화폐 단위부터 선택해 최적의 해를 찾을 수 있는 이유는 ?
A. 각 화폐 단위가 배수 관계에 속하기 때문이다.
즉, 배수 관계가 아니라면 탐욕 알고리즘으로 최적의 해를 구할 수 없다.
이말을 반증하기 위해, 다른 예시를 들어보자.
Q. 120원을 거슬러 주어야할 때, 80원, 60원, 10원의 동전이 있다면?
A. 탐욕 알고리즘 : 80원부터 거슬러주면 총 5개 동전 필요
A. 최적의 해 : 60원 X 2개로, 총 2개의 동전 필요
→ 각 화폐 단위가 배수관계에 속하지 않기 때문에, 탐욕 알고리즘으로 최적의 해를 구할 수 없다.
💡 결론
거스름돈 문제에서 각 화폐의 단위는 서로 배수 관계였기 때문에, 탐욕 알고리즘으로 최적의 해를 보장할 수 있었다. 즉, 가치가 큰 동전은 가치가 작은 동전들의 합으로 표현될 수 있다는 뜻이다.
따라서 탐욕 알고리즘으로 풀땐, 내가 선택한 해법이 어떻게 최적의 해를 보장할 수 있는지 정당성을 분석하는 과정이 필요하다.
