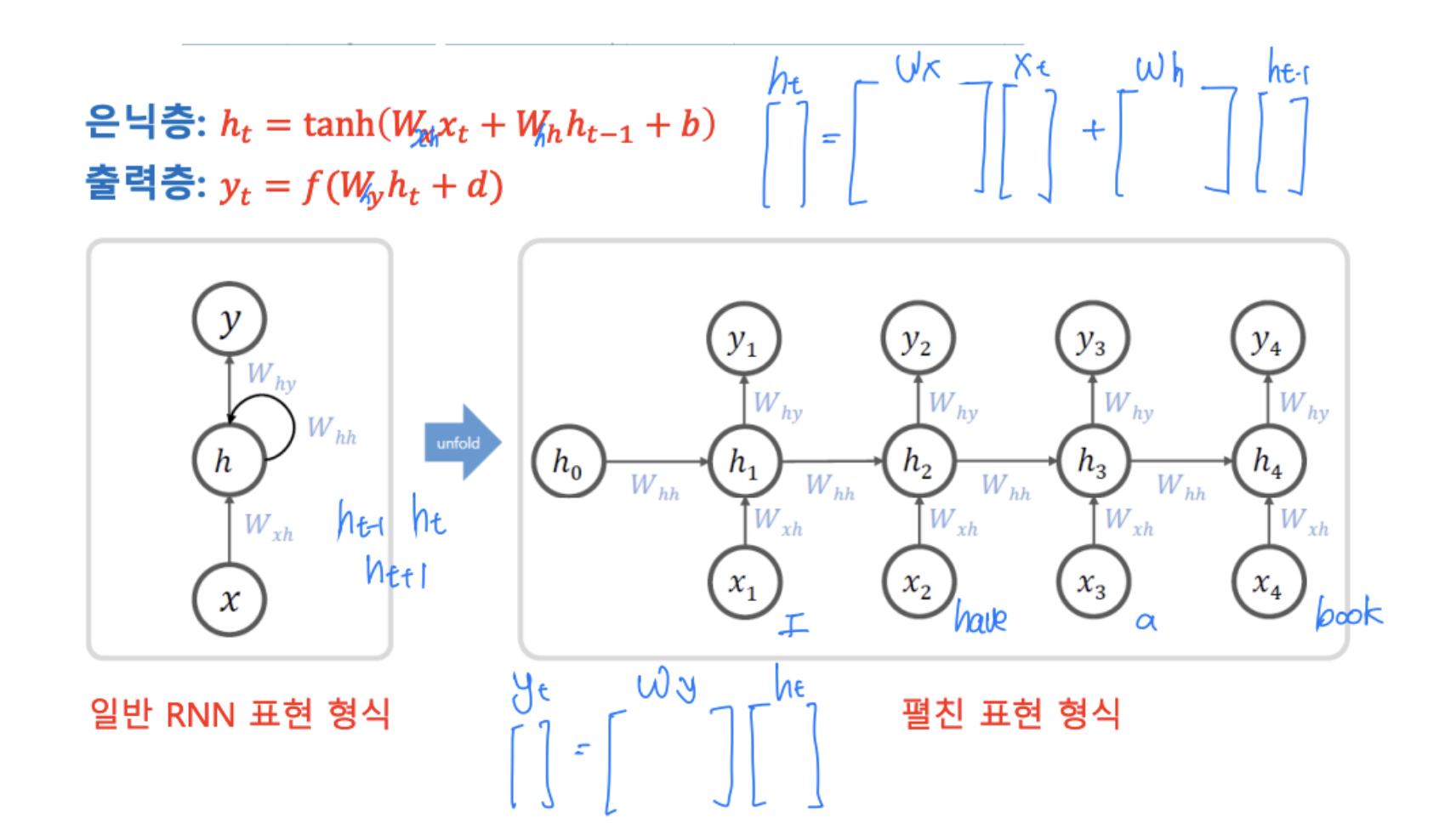
RNN
Recurrent neural network (RNN) : 입력과 출력을 sequence 단위로 처리하는 순환 신경망
- 언어는 시간상으로 펼쳐지는 데이터 형태를 가지고 있어서 RNN으로 종종 처리됨
- 개선된 형식으로는 LSTM (Long short-term memory), GRU(Gated recurrent unit) 등이 있음
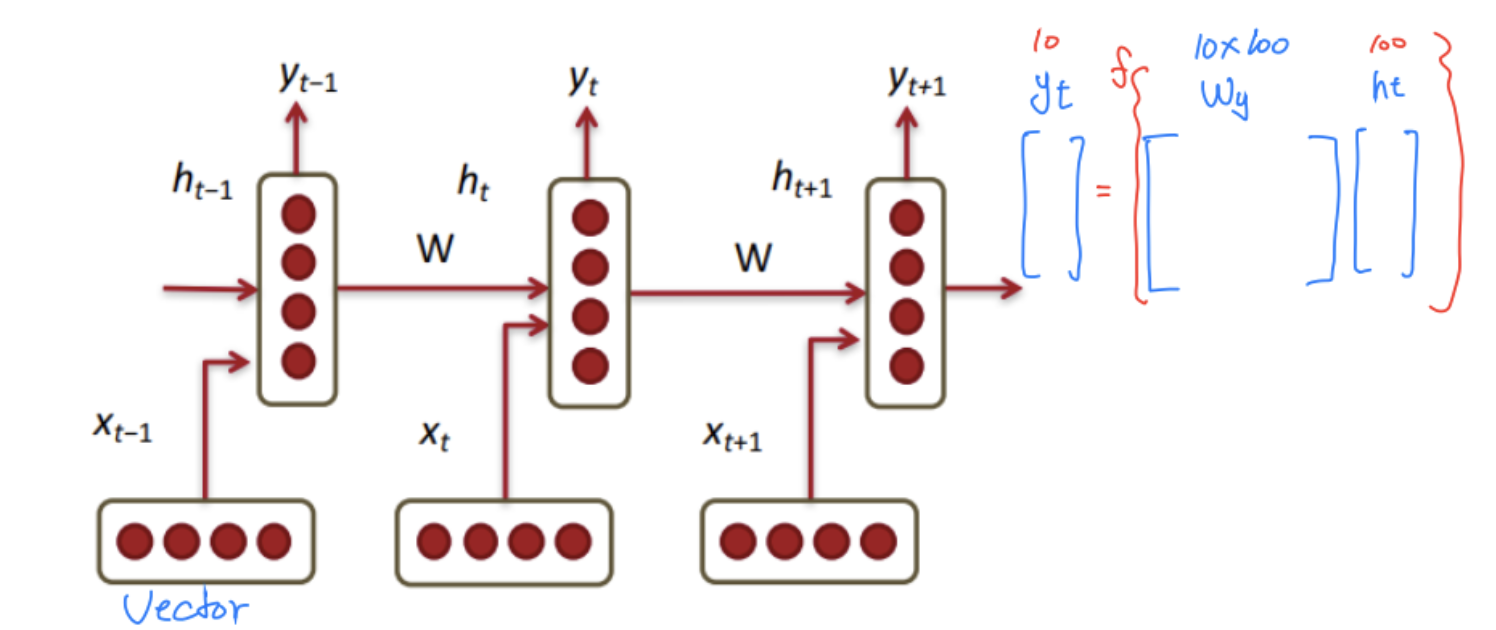
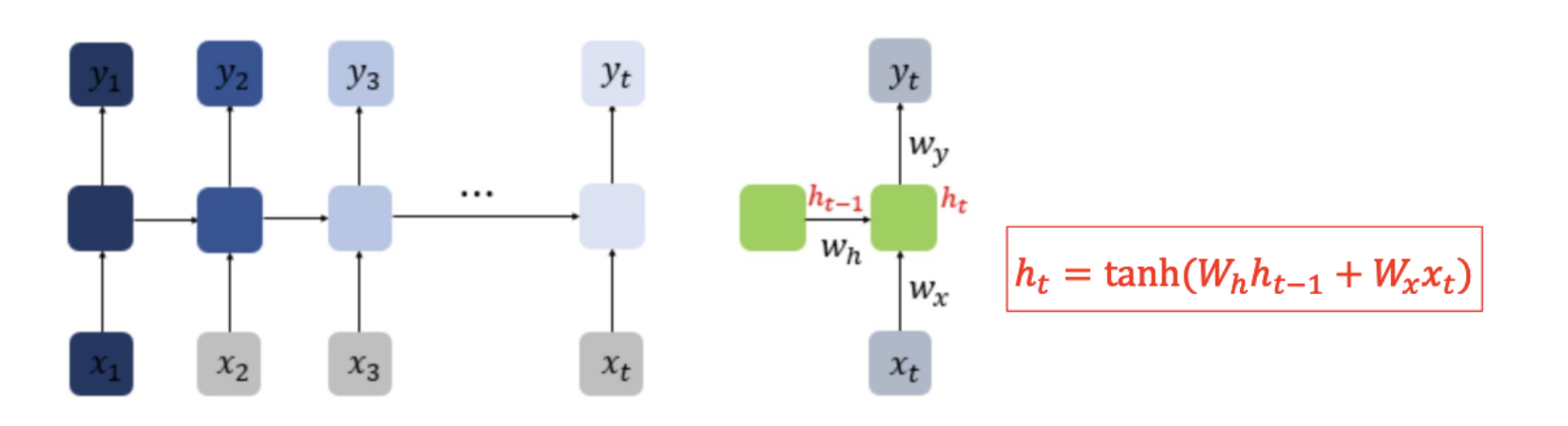
- RNN 기본 구조
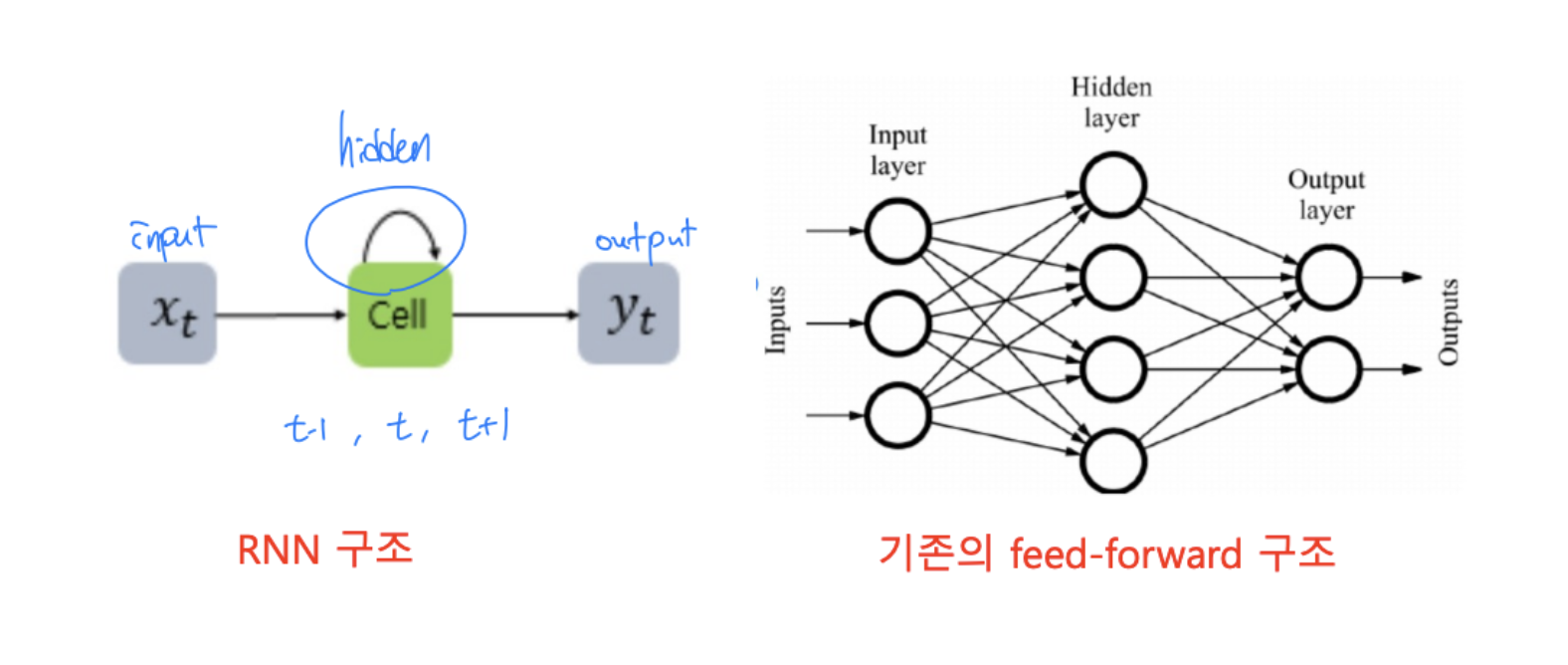
- RNN에서는 은닉층 값을 다음 상태로 전송하는 구조를 가지고 있음
- 은닉층 셀은 이전 상태의 영향을 받으므로 memory cell이라고도 함
- 은닉층은 여러 개의 셀들로 구성될 수 있음
RNN 분석 대상
- 언어, 음성, 음악, 주가지수, 날씨 등 시간에 따라 변하는 신호는 RNN 방식으로 분석할 수 있음
RNN 모델 종류
- Many-to-One 구조
- Spam mail 분류, 감성분석(sentiment analysis) 등에 사용
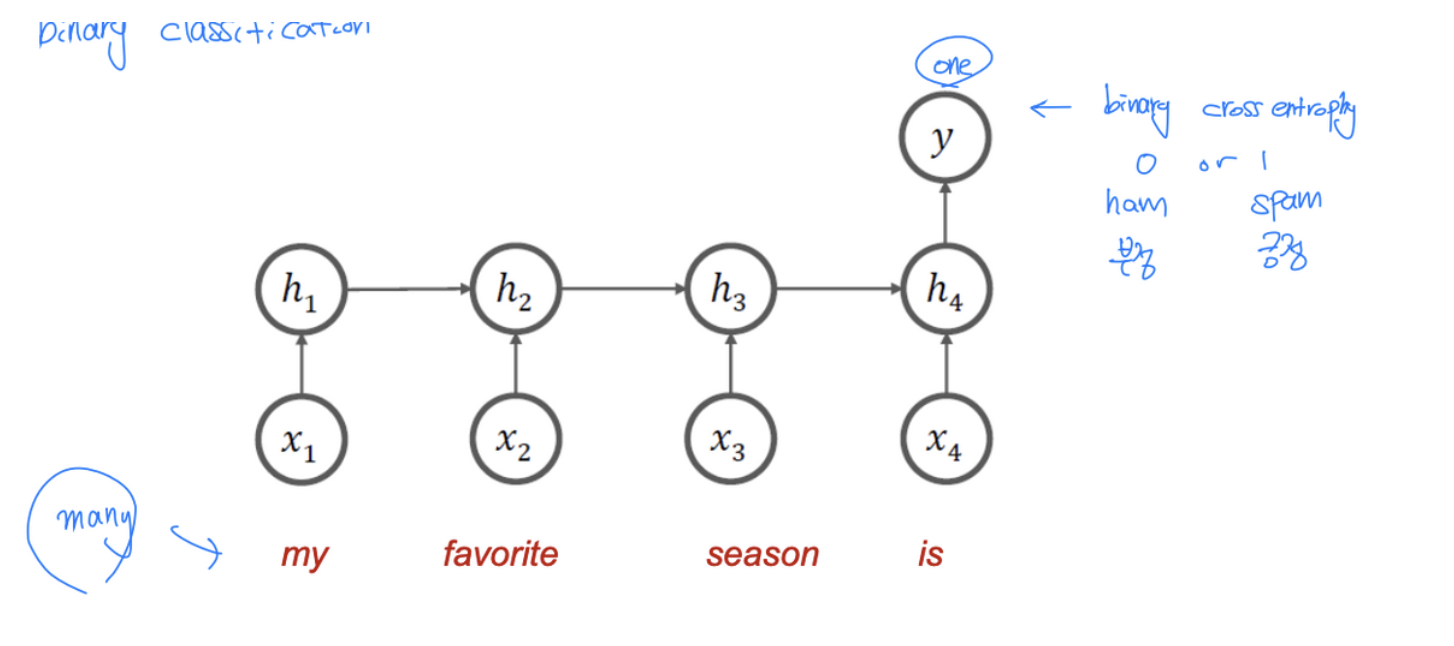
- Spam mail 분류, 감성분석(sentiment analysis) 등에 사용
-
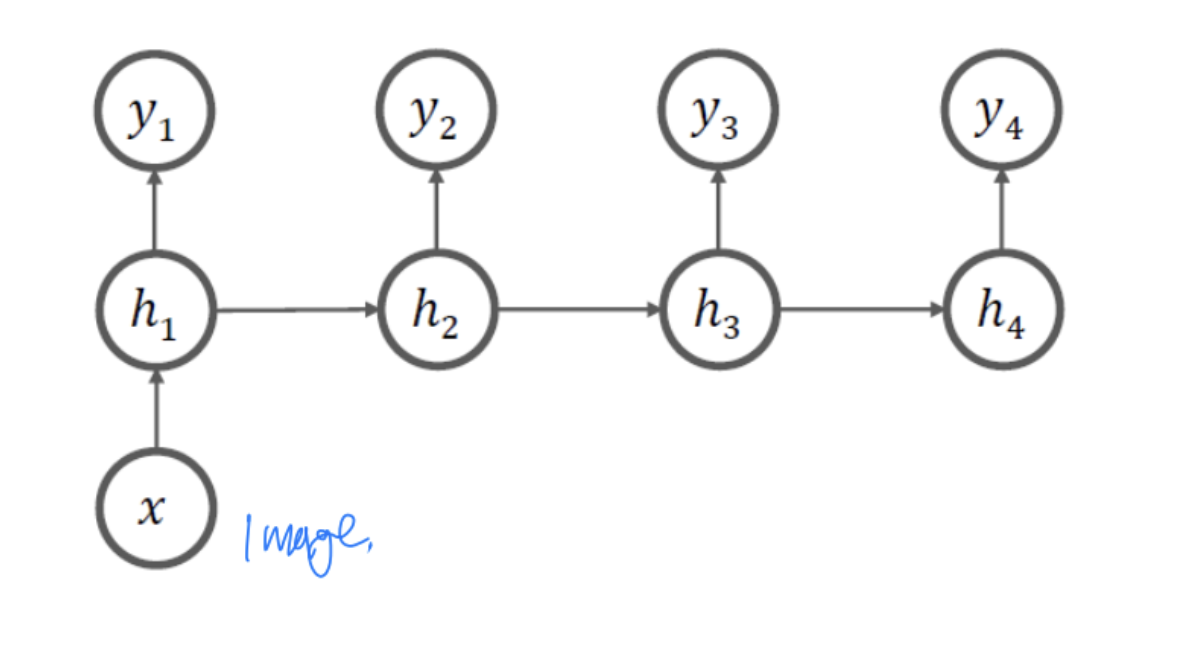
Many-to-Many 구조
-
문서 생성 등에 사용 (NLG)
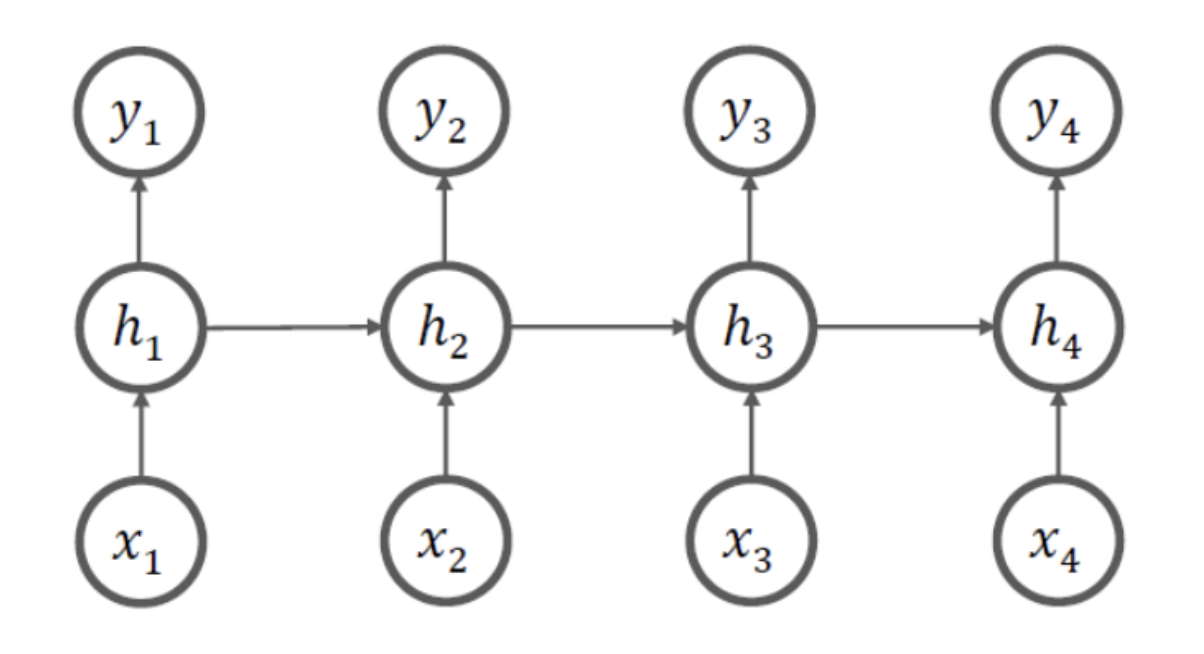
-
-
One-to-Many 구조
- 영상에서 설명문을 유추하는 Image captioning 등에 사용
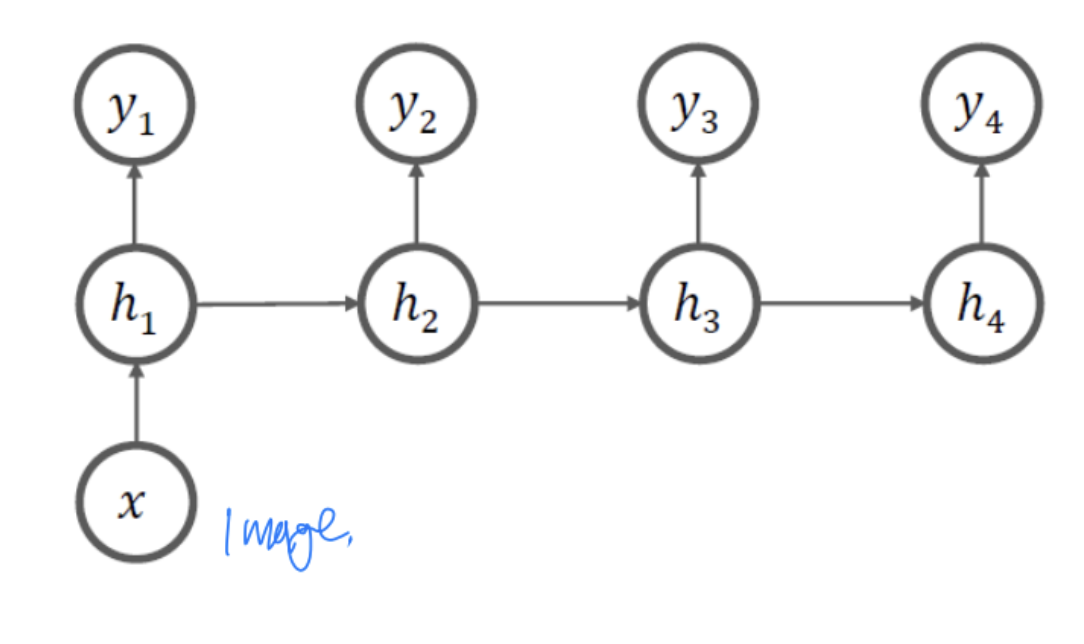
- 영상에서 설명문을 유추하는 Image captioning 등에 사용
- Bidirectional 모델
- 양방향으로 진행
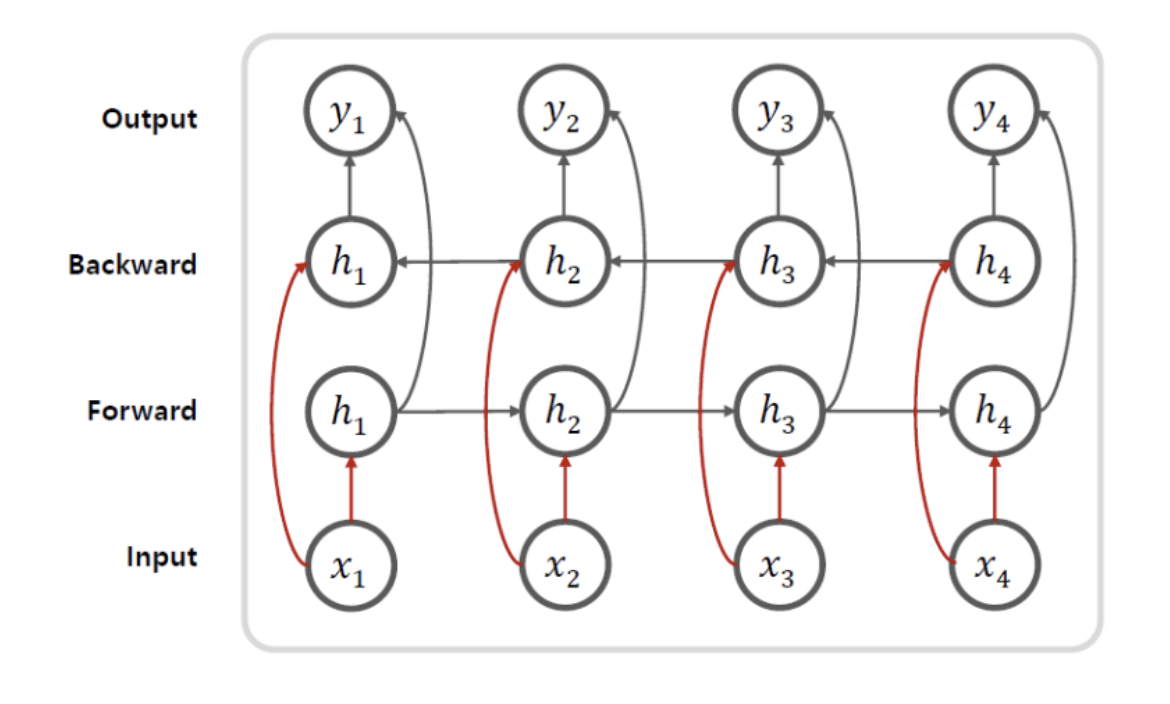
- 양방향으로 진행
- Encoder-decoder (sequence-to-seq
- 기계 번역에 사용
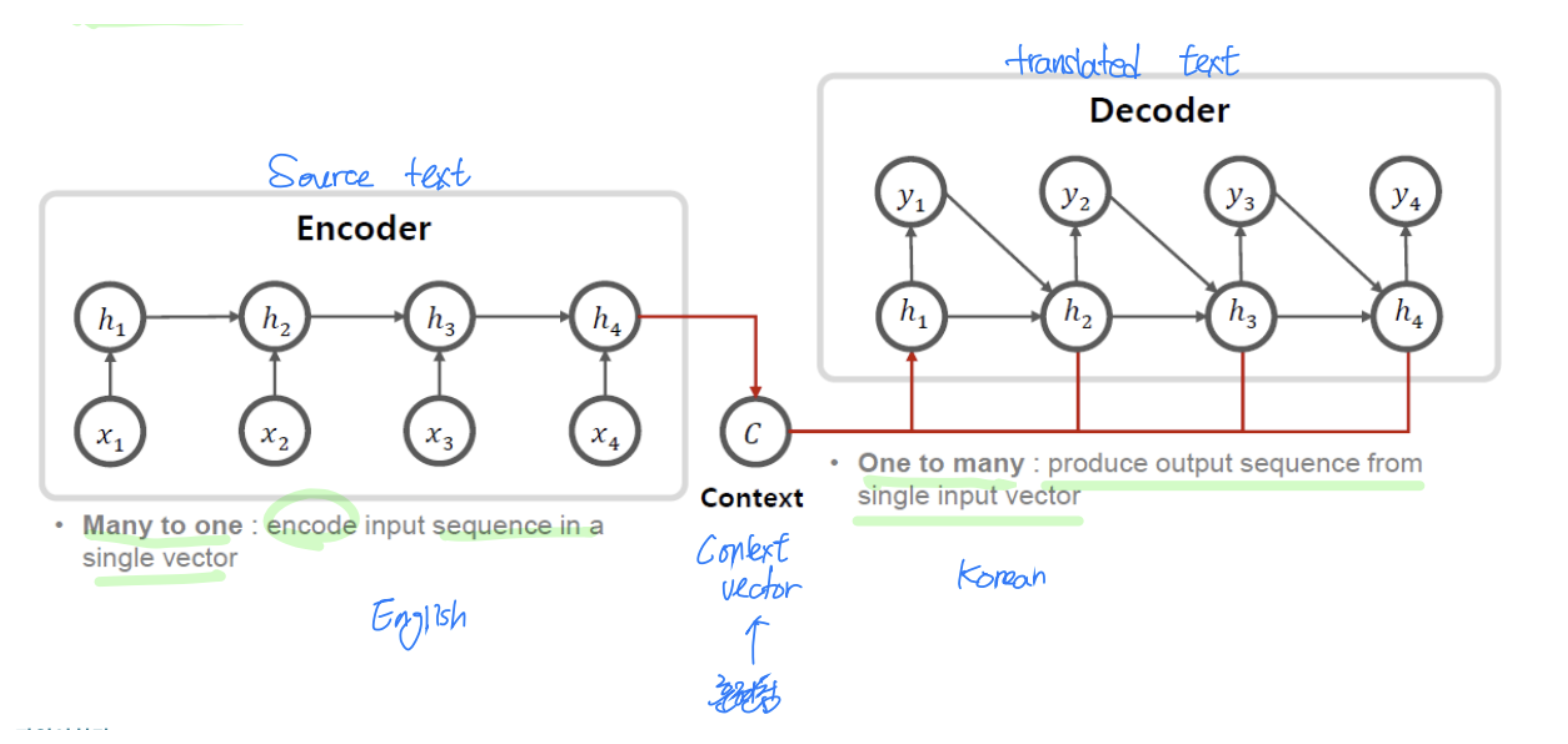
- 기계 번역에 사용
RNN의 수식 표현
- 은닉층
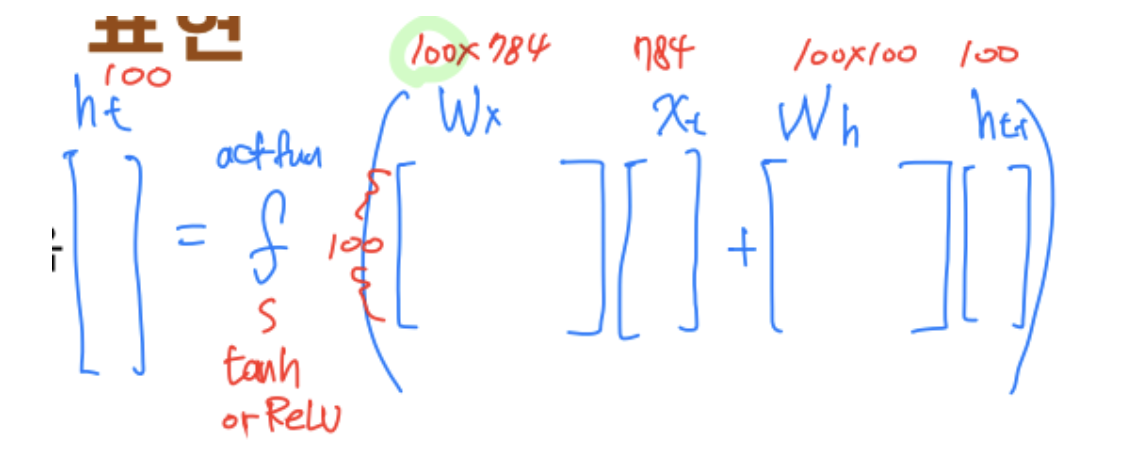
- 활성화 함수는 tanh 대신 ReLU를 사용하는 경우도 있음
- 출력층
- 는 비선형 활성화 함수
- 입력 와 은닉층 는 모두 일반적으로 벡터임
- but, 차원의 크기는 다를 수 있음 (은닉층 조절 가능)
- but, 차원의 크기는 다를 수 있음 (은닉층 조절 가능)
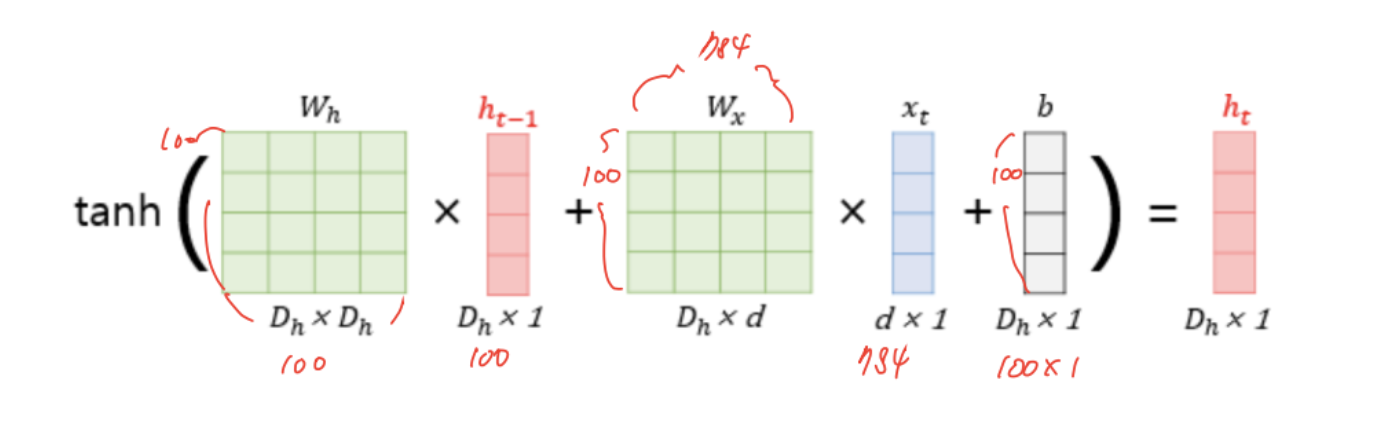
- 입력 벡터의 차원이 , 은닉층의 크기를 라 했을 때
-
-
-
-
-
RNN에서 미지수는 W_x, W_h, b 이므로
파라미터 개수는 이다.
예시 :
-
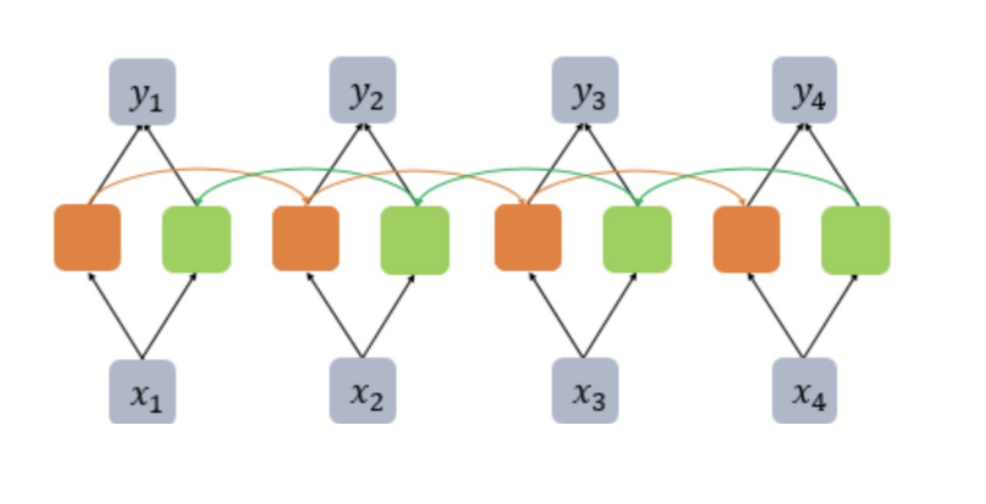
양방향(Bidirectional) RNN
- 양방향 RNN의 필요성: 문제를 풀기 위해 나중에 나오는 단어들도 필요한 경우가 있음
- Exercise is very effective at [ ] belly fat.
- reducing 2) increasing 3) multiplying
- RNN을 양방향으로 구현하는 방식도 사용되고 있음
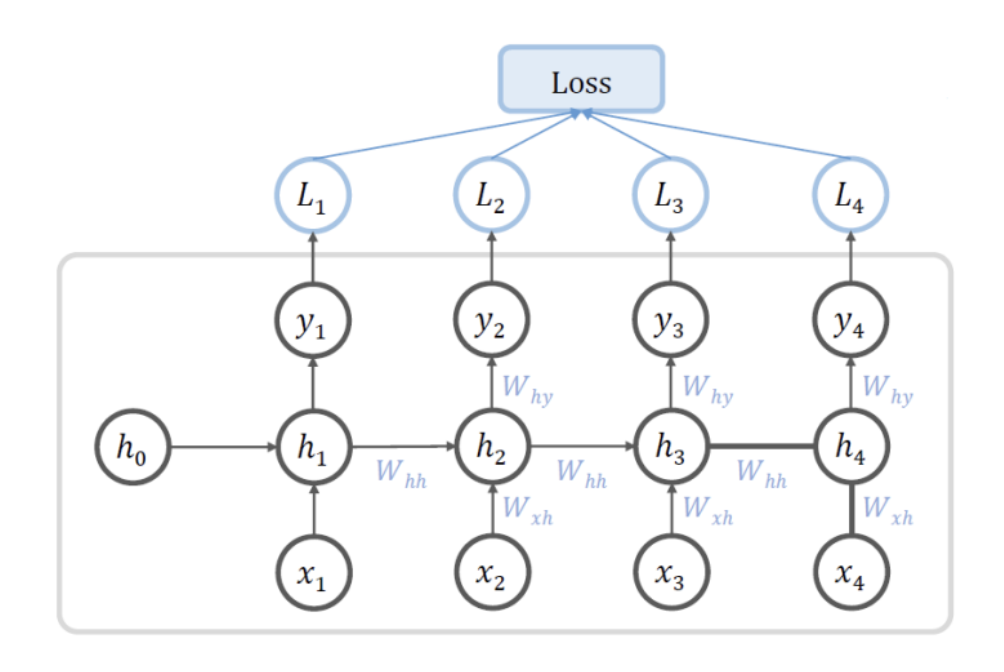
RNN의 손실은 일반적으로 입력 가 들어올 때 마다 를 계산
Backpropagation
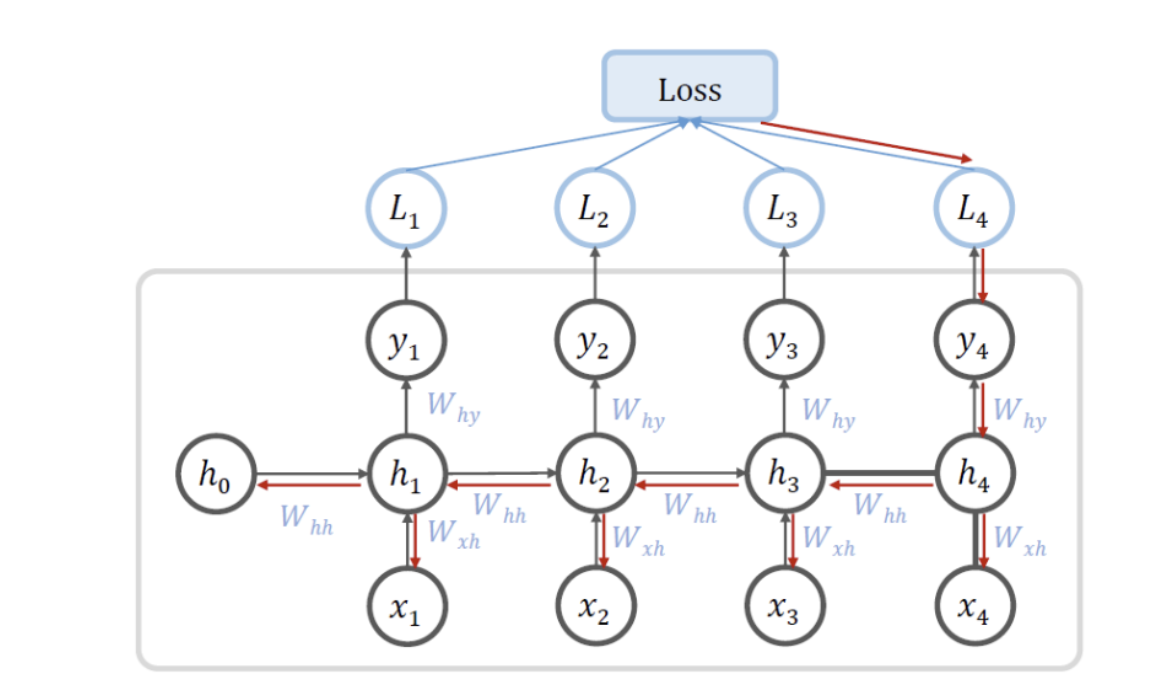
- 한 문장과 같은 일정한 데이터가 들어오면 Backprop에 의해 파라미터를 갱신함
- Backprop은 이전 단계로 전파되어야 함
Backpropagation through time(BPTT)
- 한 문장과 같은 일정한 데이터가 들어오면 Backprop에 의해 파라미터를 갱신.
- 이 과정은 처음 단계까지 전파되어야 함
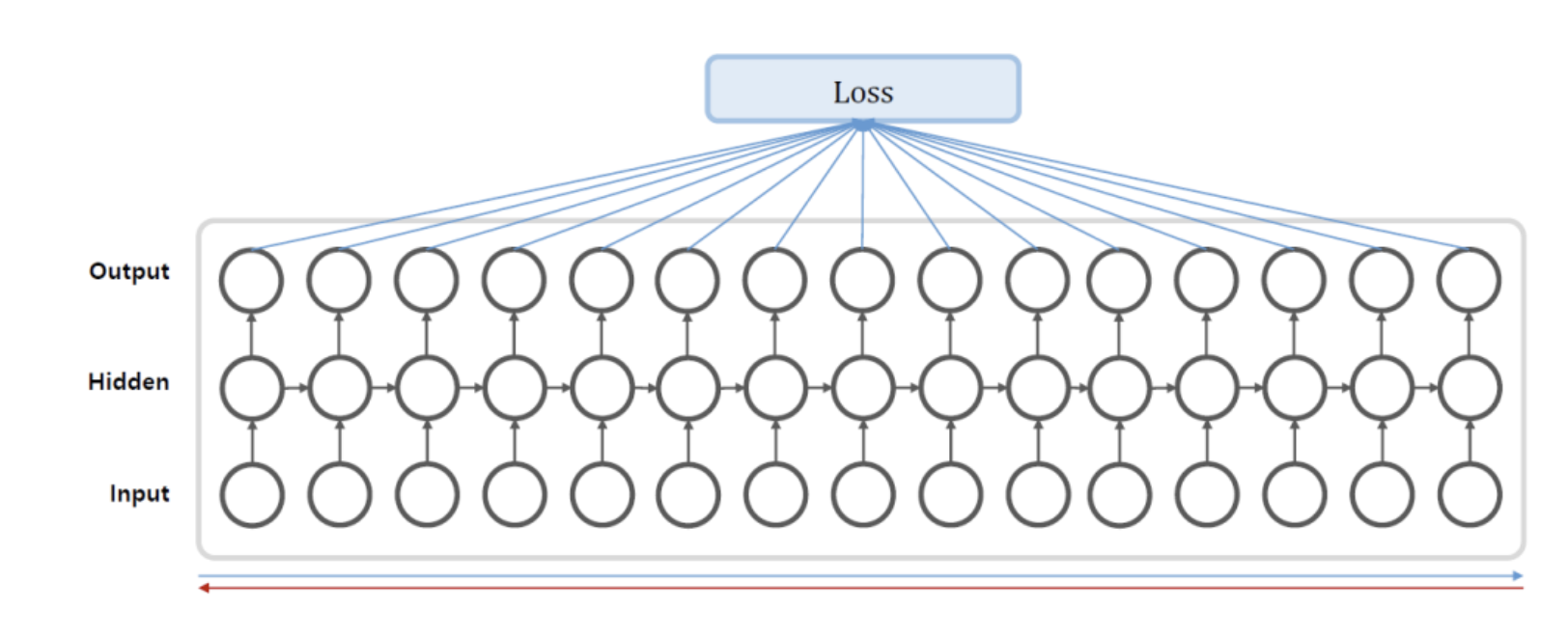
Truncated BPTT
- 계산 시간 절약을 위해 backprop 전파 단계를 일정 숫자로 제한
LSTM
기본(Vanilla) RNN의 한계
- 은닉층에서
vanishing gradient문제로 인해 이전 단어의 영향력이 오래 지속되지 못함: 아
래 그림과 같이 시간이 지나면서 영향력이 줄어듦 - 언어에서는 단어의 영향력을 보다 오랫동안 유지해야 하는 경우가 많음
(장기 의존성 문제: Long-term dependencies) - Vanishing gradient 사례 아래와 같이 계산되는 신경망에서 을 구하는 상황을 고려
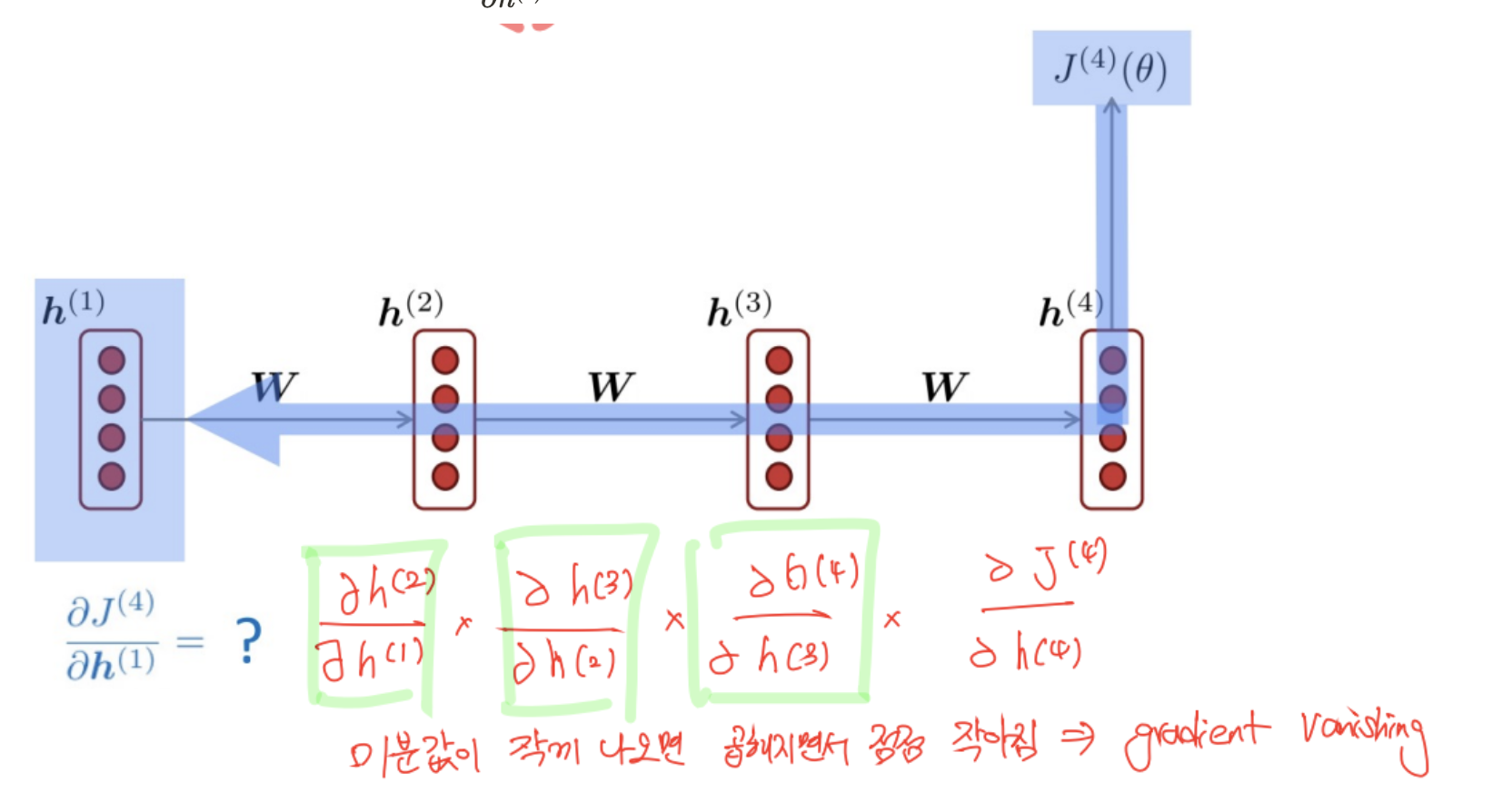
- 계산 과정에서 chain rule이 사용됨
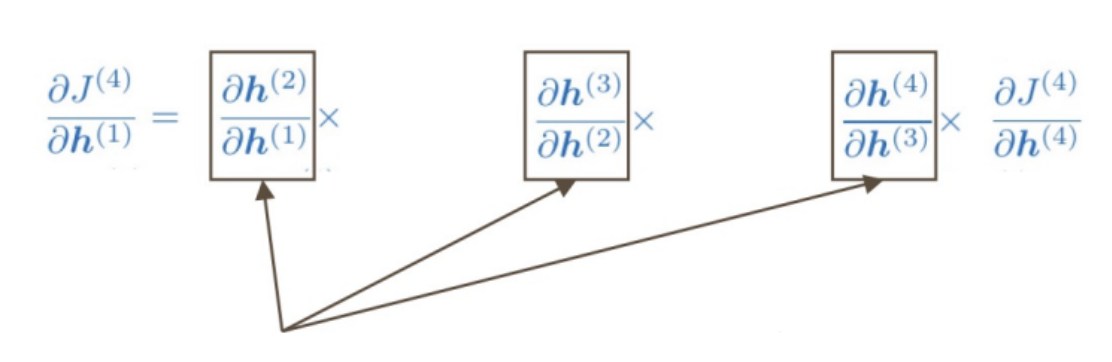
- 이 값들이 작으면 역전파가 진행될수록 gradient가 사라지게 됨
Gradient vanishing/exploding
- RNN에서는 진행할 때마다 W 행렬이 계속 곱해짐
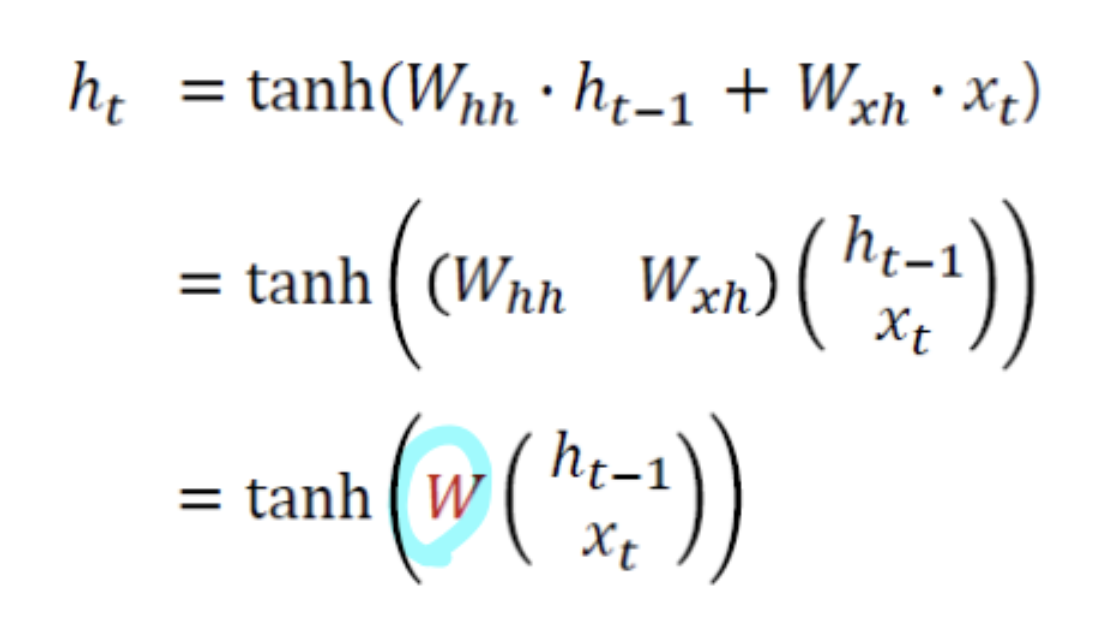
- Backprop시에도 이전 단계로 갈 때마다 W가 곱해짐
- 이러한 성질에 의해 이전 단계로 갈수록 데이터 전파가 어려워지게 됨
- 이러한 한계를 극복하는 수단으로 LSTM과 GRU가 제안되었음
LSTM (Long short-term memory)
- 기본 RNN의 장기 의존성 문제를 해결하기 위해 불필요한 기억을 지우고 기억해야 할 것을 정하는 기법
- 긴 시퀀스의 입력을 처리하는데 좋은 성능을 보임
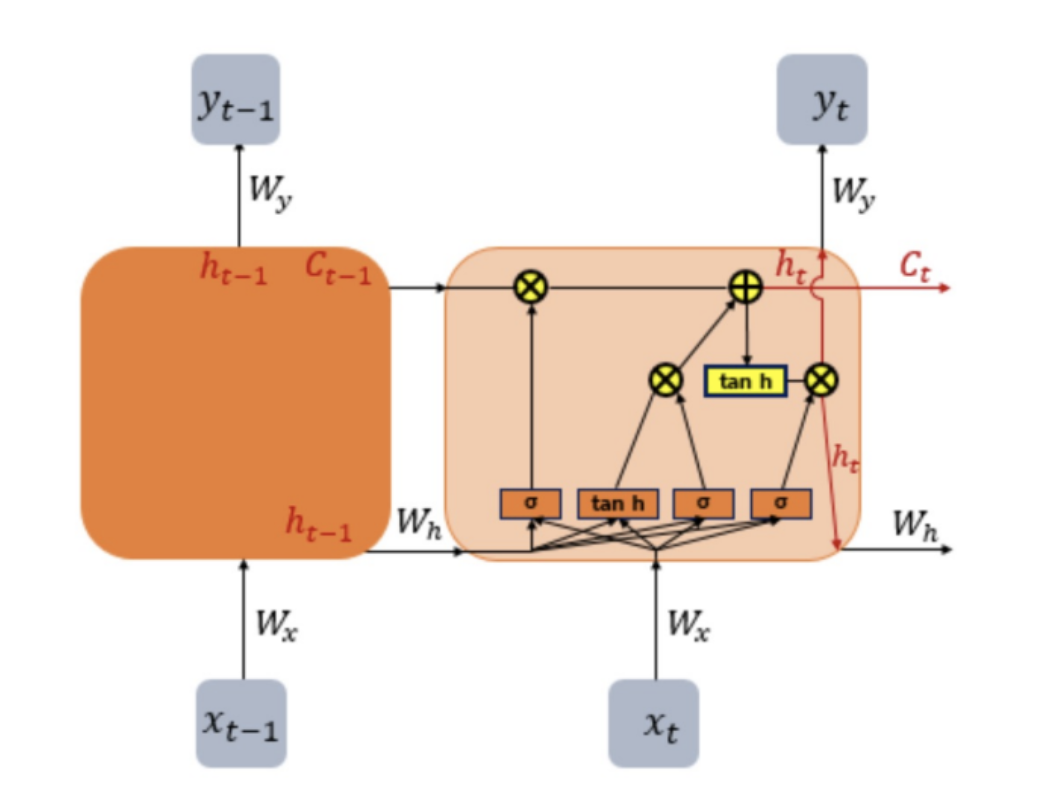
LSTM 동작 방식
- 은닉층에서 (hidden state) 이외에 셀 상태(cell state)를 나타내는 를 가지고 있음
- 와 를 구하기 위해 삭제, 입력, 출력 등 세 개의 게이트값을 활용함
- LSTM은 RNN에 비해 훈련시켜야 하는 파라미터의 개수가 4배로 많아짐
- LSTM은 기계번역, 문서분류, 문서 요약 등에서 기본 RNN에 비해 우수한 성능을 보이고 있음
- LSTM과 유사한 성능을 가지며 보다 단순한 구조로 GRU(Gated recurrent unit)도 제안되어 있음
- RNN의 한계: Vanishing gradient 문제로 인해 이전 단어의 영향력이 오래 지속되지 못함. 아래 그림과 같이 시간이 지나면서 영향력이 줄어듦
- 이 문제는 backpropagation 과정에서 가 계속 곱해지면서 결과가 점점 0으로 수렴되면서 발
생하는 것임
⇒ 이 문제를 해결하기 위한 구조로 LSTM이 제안되었음
LSTM 구조
- RNN과 달리 두 개의 상태변수 , 를 가짐
- Backpropagation에서 가 곱해지지 않는 구조로 만듦
- (cell state)
는 오래 전파되어야 하는장기 기억, $h_t$ (hidden state)는단기 기억`을 나타냄 - : t시점의 셀 상태, : t 시점의 은닉층 값
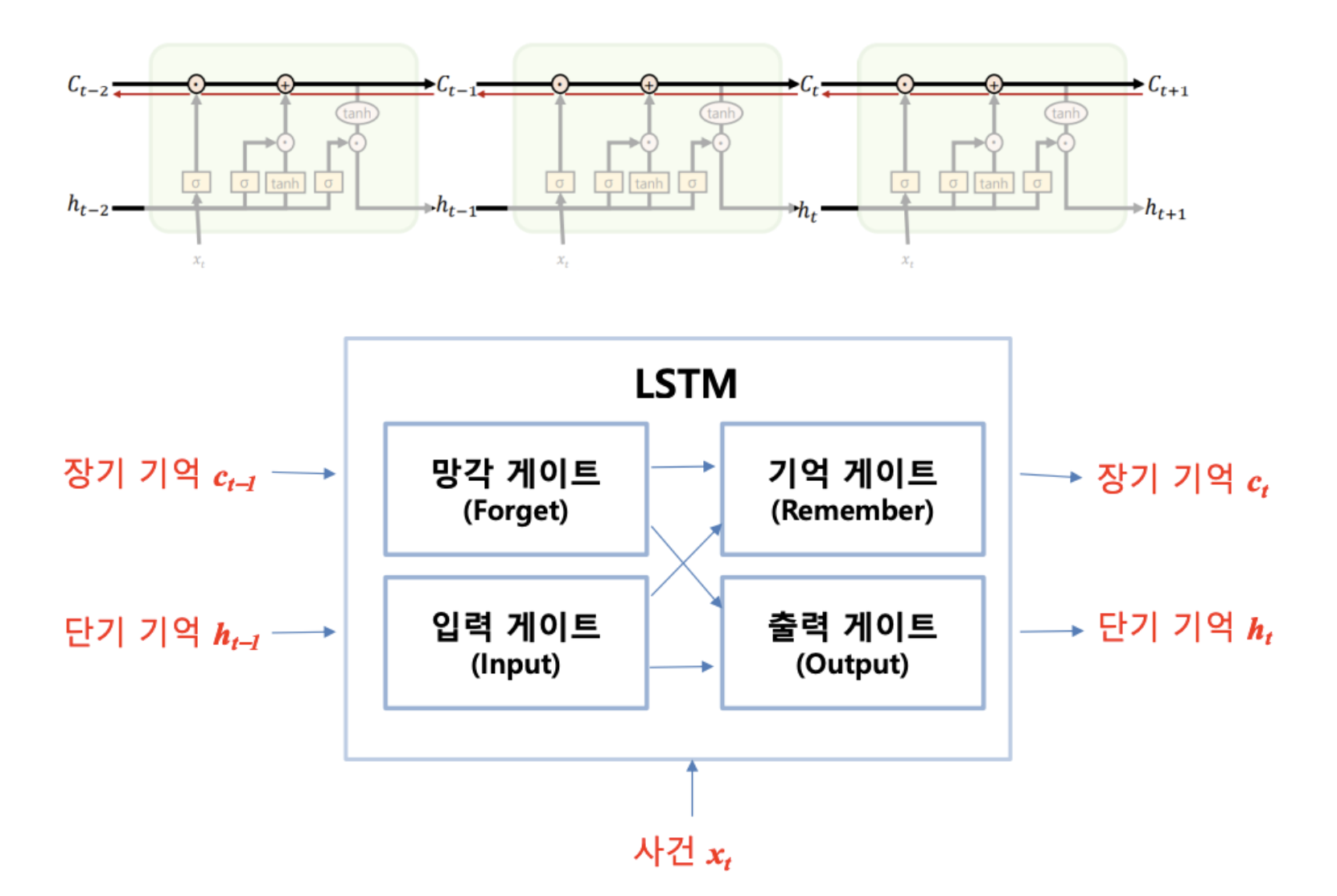
- LSTM 게이트들을 이용하여 단기와 장기 기억을 어느 정도 활용하는지를 결정
- 이전 단에서의 입력
- 현재 단에서의 입력
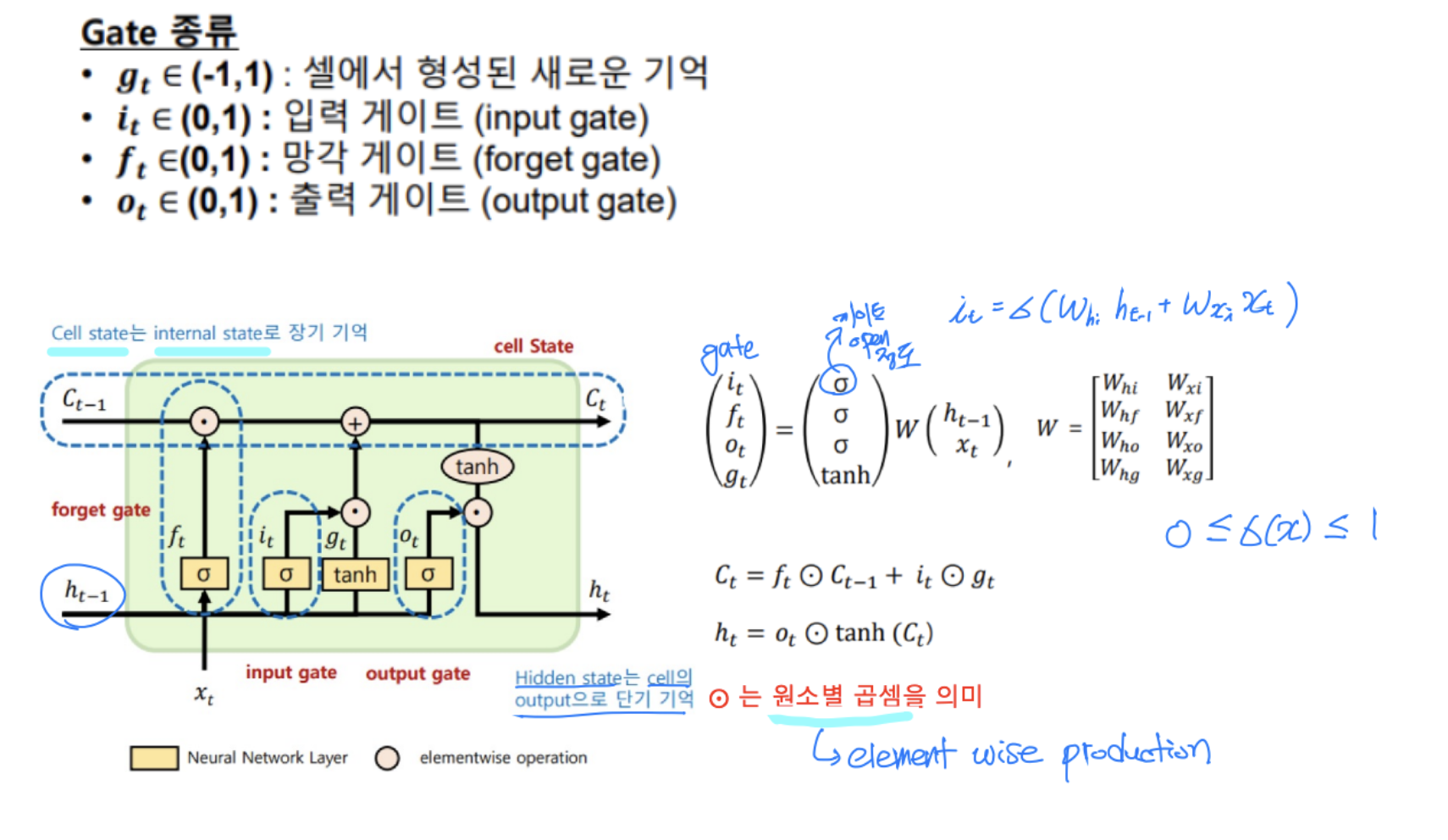
- 게이트 값 계산
- 인풋 게이트 :
- forget 게이트 :
- 아웃풋 게이트 :
- 파라미터 개수가 8개
- forget gate ⇒ 0 or 1
- 출력 계산
- : element wise ⇒ 원소별 곱셈
-
일반적으로 LSTM은 RNN에 비해 장기 기억에서 성능이 더 우수한 것으로 평가됨
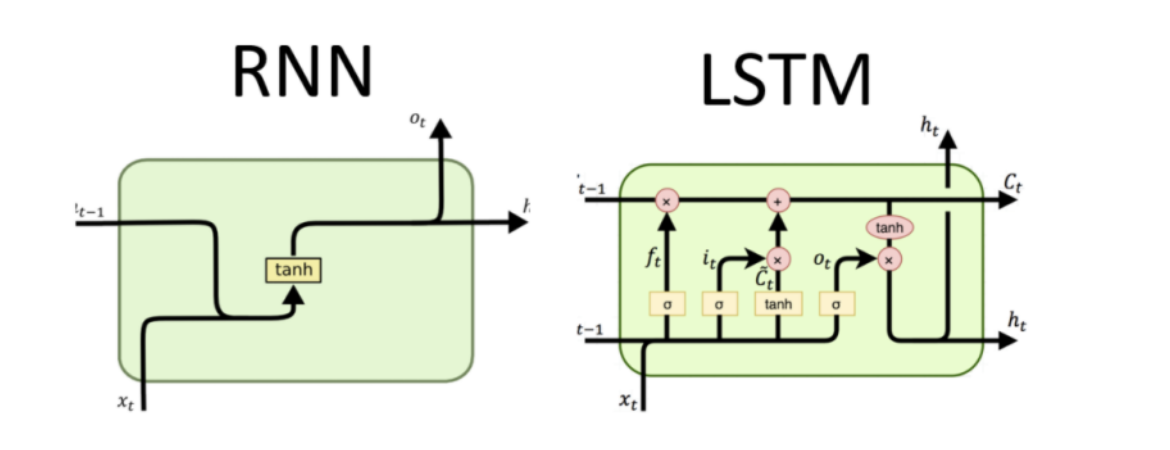
-
RNN의 경우 셀당 파라미터의 숫자는 RNN의 경우 2개(와 )이나 LSTM은 8개( ~
~)이므로 더 많은 훈련 데이터가 필요 -
입력 벡터의 차원이 , 은닉층의 크기를 라 했을 때
-
-
-
-
-
LSTM에서 미지수는 W_x, W_h, b 이므로
파라미터 개수는 이다.
-
케라스에서 RNN과 LSTM을 생성할 때 파라미터 숫자를 비교해보면 다음과 같음

