[CodeGate2023] secure primeGenerator

chall

from Crypto.Util.number import *
from hashlib import sha256
import os
import signal

BITS = 512

def POW():
    b = os.urandom(32)
    print(f"b = ??????{b.hex()[6:]}")
    print(f"SHA256(b) = {sha256(b).hexdigest()}")
    prefix = input("prefix > ")
    b_ = bytes.fromhex(prefix + b.hex()[6:])
    return sha256(b_).digest() == sha256(b).digest()

def generate_server_key():
    while True:
        p = getPrime(1024)
        q = getPrime(1024)
        e = 0x10001
        if (p-1) % e == 0 or (q-1) % e == 0:
            continue
        d = pow(e, -1, (p-1)*(q-1))
        n = p*q
        return e, d, n

# Generate N = (p1+p2) * (q1+q2) where p2 and q2 are shares chosen by the client
def generate_shared_modulus():
    SMALL_PRIMES = [2, 3, 5, 7, 11, 13]
    print(f"{SERVER_N = }")
    print(f"{SERVER_E = }")

    p1_remainder_candidates = {}
    q1_remainder_candidates = {}    
    # We prevent p1+p2 is divided by small primes
    # by asking the client for a possible remainders of p1
    for prime in SMALL_PRIMES:
        remainder_candidates = set(map(int, input(f"Candidates of p1 % {prime} > ").split()))
        assert len(remainder_candidates) == (prime+1) // 2, f"[-] wrong candidates for {prime}"
        p1_remainder_candidates[prime] = remainder_candidates
    
    while True:
        p1 = bytes_to_long(os.urandom(BITS // 8))        
        for prime in SMALL_PRIMES:
            if p1 % prime not in p1_remainder_candidates[prime]:
                break
        else:
            break
    
    # and same goes for q1
    for prime in SMALL_PRIMES:
        remainder_candidates = set(map(int, input(f"Candidates of q1 % {prime} > ").split()))
        assert len(remainder_candidates) == (prime+1) // 2, f"[-] wrong candidates for {prime}"
        q1_remainder_candidates[prime] = remainder_candidates
    
    while True:
        q1 = bytes_to_long(os.urandom(BITS // 8))
        
        for prime in SMALL_PRIMES:
            if q1 % prime not in q1_remainder_candidates[prime]:
                break
        else:
            break

    p1_enc = pow(p1, SERVER_E, SERVER_N)
    q1_enc = pow(q1, SERVER_E, SERVER_N)    

    print(f"{p1_enc = }")
    print(f"{q1_enc = }")
    X = list(map(int, input("X > ").split()))
    assert len(X) == 12
    
    N = (p1*q1 + sum(pow(x, SERVER_D, SERVER_N) for x in X)) % SERVER_N
    assert N.bit_length() >= 1024, f"[-] too short.., {N.bit_length()}"

    print(f"{N = }")
    
    return p1, q1, N

# check whether N is a product of two primes
def N_validity_check(p1, q1, N):
    for _ in range(20):
        b = bytes_to_long(os.urandom(2 * BITS // 8))
        print(f"{b = }")
        client_digest = input("Client digest > ")
        server_digest = sha256(long_to_bytes(pow(b, N+1-p1-q1, N))).hexdigest()
        if server_digest != client_digest:
            print("N is not a product of two primes I guess..")
            return False
        else:
            print("good!")
     
    return True

if not POW():
    exit(-1)

signal.alarm(60)
SERVER_E, SERVER_D, SERVER_N = generate_server_key()
p1, q1, N = generate_shared_modulus()
if not N_validity_check(p1, q1, N):
    exit(-1)

FLAG = open("flag", 'rb').read()
FLAG += b'\x00' + os.urandom(128 - 2 - len(FLAG))
FLAG_ENC = pow(bytes_to_long(FLAG), 0x10001, N)

print(f"{FLAG_ENC = }")

• POW() : b.hex()[6:] 주어짐, sha256(b).digest()와 같은 b 찾아야함

• $2, 3, 5, 7, 11, 13$에 대하여 각 $prime$으로 나눈 나머지 후보를 $(prime+1)//2$개 입력, 이를 만족하도록 $p1$, $q1$ 각각 생성

• x 12번 입력 → $p1q1 + ∑(x^{server_d} \ (mod \ server_n)) = n$

• $n$, $p1$, $q1$ 주어짐

• $b$ 주어짐, $b^{n+1-p1-q1} \ (mod \ n)$ 20번 맞추면 for문 통과

• for문 통과한 뒤, $flag^{65537} \ (mod \ n)$ 주어짐
  
  
  문제에서 $(p1 + p2)(q1+q2)$ 형태로 $n$을 설정하여 풀도록 유도하고 있다. 하지만, $p1$, $q1$을 직접적으로 모르는 상황에서 $p2$, $q2$를 정해서 $ϕ(n)$을 계산할 수 있는 방법을 생각하지 못했고, 결국, 유도한 방법을 무시하고 다른 방법을 찾아보았다.
  
  
  
  

exploit strategy

• $n$은 정할 수 있고, $(n+1-p1-q1)$을 leak하여 $b^{n+1-p1-q1} \ (mod \ n)$을 계산해야함

• $p1$, $q1$의 enc값이 주어졌고, 서버에서 이를 복호화할 수 있음

→ idea : $(p1+q1)$에 대한 식으로 $n$을 정하면 됨

또한, 마지막 flag를 복호화하기 위해서 $ϕ(n)$을 계산할 수 있어야함 → $n$이 우리가 알 수 있는 소수로 이루어져 있어야함.

n.bit_length() ≥ 1024이므로 n을 적당히 $4(p1 + q1 - 1)^2$으로 잡자. ($p1+q1$ 은 짝수이므로 1을 뺐다.)

$(p1 + q1 - 1)$ 이 소수가 된다면? → $b^{n+1-p1-q1} \ (mod \ n)$계산 가능, $ϕ(n)$계산 가능 → flag leak

exploit code

고맙게도 기본적인 exploit code의 틀은 제공된 상태였다.

import gmpy
from Crypto.Util.number import *
from hashlib import sha256
from pwn import *
from itertools import product
import random

context.log_level = "debug"

def get_additive_shares(x, n, mod):
    shares = [0] * n
    shares[n-1] = x
    for i in range(n-1):
        shares[i] = random.randrange(mod)
        shares[n-1] = (shares[n-1] - shares[i]) % mod
    assert sum(shares) % mod == x
    return shares

BITS = 512

def POW():
    print("[DEBUG] POW...")
    b_postfix = r.recvline().decode().split(' = ')[1][6:].strip()
    h = r.recvline().decode().split(' = ')[1].strip()
    for brute in product('0123456789abcdef', repeat=6):
        b_prefix = ''.join(brute)
        b_ = b_prefix + b_postfix
        if sha256(bytes.fromhex(b_)).hexdigest() == h:
            r.sendlineafter(b' > ', b_prefix.encode())
            return True

    assert 0, "Something went wrong.."

def generate_shared_modulus():
    print("[DEBUG] generate_shared_modulus...")
    p2 = random.randrange(2 ** BITS, 2 ** (BITS+1))
    q2 = random.randrange(2 ** BITS, 2 ** (BITS+1))

    p2, q2 = (p2//2)*2, (q2//2)*2

    SMALL_PRIMES = [2, 3, 5, 7, 11, 13]
    # Candidates of p1
    for prime in SMALL_PRIMES:
        remainder_candidates = []
        # c = (-p2 % prime) should not be chosen
        while len(remainder_candidates) < (prime+1) // 2:
            c = random.randrange(prime)
            if c == -p2 % prime or c in remainder_candidates:
                continue
            remainder_candidates.append(c)

        r.sendlineafter(b' > ', ' '.join(str(c) for c in remainder_candidates).encode())

    # Candidates of q1
    for prime in SMALL_PRIMES:
        remainder_candidates = []
        # c = (-q2 % prime) should not be chosen
        while len(remainder_candidates) < (prime+1) // 2:
            c = random.randrange(prime)
            if c == -q2 % prime or c in remainder_candidates:
                continue
            remainder_candidates.append(c)

        r.sendlineafter(b' > ', ' '.join(str(c) for c in remainder_candidates).encode())

    p1_enc = int(r.recvline().decode().split(' = ')[1])
    q1_enc = int(r.recvline().decode().split(' = ')[1])
    p2_enc = pow(p2, SERVER_E, SERVER_N)
    q2_enc = pow(q2, SERVER_E, SERVER_N)

    X = []
    shares_a = get_additive_shares(4, 2, SERVER_N)
    shares_b = get_additive_shares(4, 2, SERVER_N)
    shares_c = get_additive_shares(7, 2, SERVER_N)
    shares_d = get_additive_shares(4, 2, SERVER_N)
    shares_e = get_additive_shares(-8%SERVER_N, 2, SERVER_N)
    shares_f = get_additive_shares(-8%SERVER_N, 2, SERVER_N)

    # N = p1*q1 + sum(pow(x, SERVER_D, SERVER_N) for x in X) = p1*q1 + p1*q2 + p2*q1 * p2*q2 = (p1+p2)*(q1+q2)
    for i in range(2):
        X.append(pow(shares_a[i], SERVER_E, SERVER_N) * p1_enc * p1_enc % SERVER_N)
        X.append(pow(shares_b[i], SERVER_E, SERVER_N) * q1_enc * q1_enc % SERVER_N)
        X.append(pow(shares_c[i], SERVER_E, SERVER_N) * p1_enc * q1_enc % SERVER_N)
        X.append(pow(shares_d[i], SERVER_E, SERVER_N) % SERVER_N)
        X.append(pow(shares_e[i], SERVER_E, SERVER_N) * q1_enc % SERVER_N)
        X.append(pow(shares_f[i], SERVER_E, SERVER_N) * p1_enc % SERVER_N)
    random.shuffle(X)

    r.sendlineafter(b' > ', ' '.join(str(x) for x in X).encode())

    N = int(r.recvline().decode().split(' = ')[1])

    return p2, q2, N

# STEP 2 - N_validity_check
def N_validity_check_client(p2, q2, N):
    print("[DEBUG] N_validity_check_client...")
    for _ in range(20):
        b = int(r.recvline().decode().split(' = ')[1])
        client_digest = sha256(long_to_bytes(pow(b, N-int(gmpy.root(N//4, 2)[0]), N))).hexdigest()
        r.sendlineafter(b' > ', client_digest.encode())
        msg = r.recvline().decode()
        if msg != "good!\n":
            print(msg)
            return -1

    flag_enc = int(r.recvline().decode().split(' = ')[1])
    return flag_enc

while(1):
    REMOTE = 1
    if REMOTE:
        r = remote("13.125.181.74", 9001)
    else:
        r = process(["python3", "./prob.py"])

    POW()
    SERVER_N = int(r.recvline().decode().split(' = ')[1])
    SERVER_E = int(r.recvline().decode().split(' = ')[1])

    p2, q2, N = generate_shared_modulus()
    flag_enc = N_validity_check_client(p2, q2, N)
    if flag_enc == -1:
        exit(-1)

    a = int(gmpy.root(N//4, 2)[0])
    print(isPrime(a))
    if isPrime(a) == True:
        print(f"{N = }")
        print(f"{flag_enc = }")
        phi = 3*(a**2 - a)
        d = inverse(0x10001, phi)
        print(long_to_bytes(pow(flag_enc, d, N)))
        break
r.interactive()

p2, q2는 문제풀이 과정에서 필요없지만, 결국 candidate으로 뭐든 입력해야 하니, 그냥 남겨두었다.

이제 $(p1 + q1 - 1)$이 소수가 될 때까지 기다리면 된다.

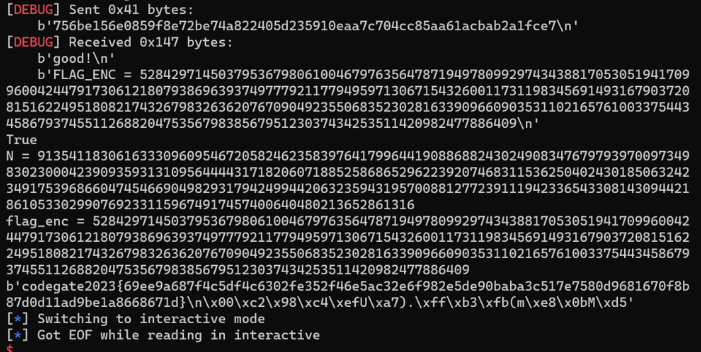
언인텐 같지만 어쨌든 풀었으니 꽤 뿌듯하다🔥🔥