ELLIPTIC CURVES Background & Pohlig-Hellman attack

이 글은 cryptohack 및 https://wstein.org/edu/2010/414/projects/novotney.pdf 을 바탕으로 작성되었다.

EC는 기존 RSA 암호의 대안으로 제안된 공개키 방식이다. 256-bit EC key는 3072-bit RSA key와 같은 효과를 지닌다고 한다.

용어 정리

*군 중 교환법칙이 성립하는 군을 아벨 군이라고 한다.

*trapdoor function이란 단방향 함수의 한 종류로 함수의 역을 구하는 것은 어렵지만, trapdoor라고 불리는 특수한 정보가 있으면 쉽게 역을 구할 수 있는 함수이다. (ex. RSA에서 d가 trapdoor이다.)

EC Background

ECC는 RSA, Diffie-Hellman과 같은 비대칭 암호화 프로토콜이다.

RSA의 trapdoor function은 소인수분해의 어려움에 기반을 두고 있고, Diffie-Hellman은 DLP에 기반을 두고 있다. 이는 모두 우리에게 익숙한 연산이지만, ECC에서의 group operation은 낯설 것이다.

타원곡선의 식은 일반적으로 다음과 같다. (바이어슈트라스 방정식)

갑자기 이런 식으로 암호화를 한다는게 뜬금없을 수 있다. 살짝의 흐름을 보자.

$aX + bY = c$ 형태의 선형 방정식은 너무나도 쉽게 풀린다. 그럼 차수를 올려서 $X^2+2XY+4Y^2=3$ 과 같은 형태를 보면, 조금 더 복잡하긴 하지만 모든 형태가 결국

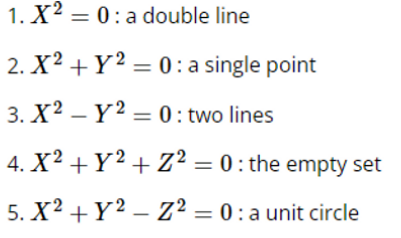
위의 5가지로 변형될 수 있다.

그럼 더 복잡한 꼴이 없을까? 하다가 나온게 타원곡선의 형태이다. 여기서 차수를 올리면 너무 어려워지고, 내리면 trivial해진다.

대충 흐름을 봤으니, 이제 타원곡선에 대하여 본격적으로 알아보자.

타원곡선에서는 특이한 연산을 정의할 수 있다. point addition으로 불리는 이 연산은 곡선에서의 두 점을 더하여 새로운 점을 얻을 수 있다. 이는 교환법칙이 성립하는 아벨군에 포함된다. 여기서 타원곡선의 trapdoor function이 등장한다.

$Q = 2P = P + P$

위와 같이 point addition의 반복은 scalar multiplication이 되고 이것이 ECC의 trapdoor function이다.

ECC의 trapdoor function은 $Q$, $P$를 알고, $Q = nP$ 가 성립할 때, $n$을 찾기 어려운 점에 기반을 둔다.

그럼 point addition은 어떻게 동작하는걸까?

$P + Q$ 를 한다 하자. $P$와 $Q$를 이어서 곡선의 새로운 점과 만나도록 그린 뒤, 새로 만나는 점을 $R$이라 하자. $R$을 $x$축에 대하여 대칭한 점이 $P + Q$의 결과가 된다. 즉, $P + Q = R' = R(x, -y)$

$P + P$ 를 하는 경우에는 $P$에서의 접선을 그려서 똑같이 하면 된다.

그렇다면, $P$와 $Q$를 이었는데 곡선과 만나지 않는다면 어떻게 될까? 이런 경우에는 무한대 점 $O$ 를 정의하여 $P + Q = O$ 가 된다. $O$는 덧셈에 대한 항등원이 된다. $( P + O = P )$

이를 그림으로 보자.

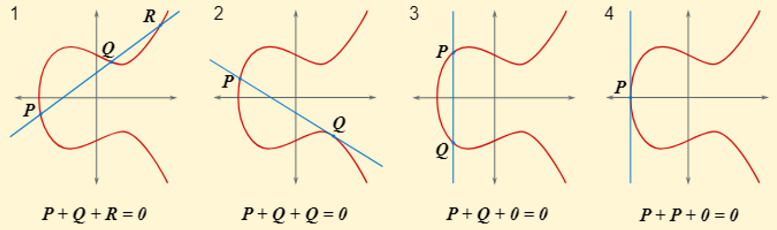
타원곡선 $E$는 아래와 같이 바이어슈트라스 방정식의 해집합으로 정의한다. ( $O$ 도 포함 ) 여기서 두 번째 조건은 특이점이 없기 위한 조건이다.

Pohlig-Hellman algorithm

이제 타원곡선에서의 DLP인 ECDLP(Elliptic Curve Discrete Logarithm Problem)가 무엇인지 알아보자. ECDLP란, $Q = nP$ 이고, $Q$와 $P$를 알 때, $n$을 찾기 어렵다는 문제이다. ECDLP에 대한 공격기법 중 하나인 Pohlig-Hellman algorithm을 알아보자.

$p$가 smooth prime인 경우, DLP가 Pohlig-Hellman algorithm에 의해 쉽게 풀리는 것은 이미 알고 있다. 일반적인 DLP에서의 Pohlig-Hellman algorithm은 다음과 같다.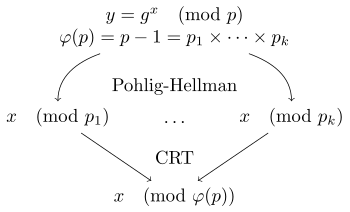

좀 더 일반적으로 생각해보면, $y$에 대한 $group$에서 $ϕ(n)$은 $order$이고, $order$이 작은 소인수들로 소인수분해되면 어느 $group$에서나 Pohlig-Hellman algorithm을 사용할 수 있다. EC는 $group$ 중에서도 $Abelian \ group$임을 앞서 언급했으니, EC에서도 Pohlig-Hellman algorithm를 적용할 수 있다..!


*여기서 타원곡선이 항상 $order$을 가지려면 순회해야 하는데, 그럴거라는 보장이 있는지 의문이 들 수 있다. (필자의 생각은, 점$P$가 있다면, $-P$도 존재하므로 $P$를 계속 더하다보면 $-P$가 되고 그 다음 $O$, $P$가 되어 무조건 순회하는 것 같다.) 이 의문을 포함하여 EC의 $order$을 계산하는 방법과 같은 구체적인건 나중에 공부하자.

이미 Pohlig-Hellman algorithm의 작동 방식은 알고 있으니, 코드를 통해 과정을 적어보자. (Cryptohack의 smooth criminal문제를 예시로 들겠다.)

우선, 주어진 $P$와 $Q$, 그리고 $P$, $Q$를 generate한 $G$를 정의하고 EC $(y^2 = x^3+ax+b)$의 $order$을 구해야 한다.

E = EllipticCurve(GF(p), [a, b])
P = E.point(P)
Q = E.point(Q)
G = E.point(G)
factor(E.order()) #2^2 * 3^7 * 139 * 165229 * 31850531 * 270778799 * 179317983307

EC의 $order$을 $n$이라 했을 때, Pohlig-Hellman algorithm으로 ECDLP가 풀리려면 $n$이 작은 소인수들로 소인수분해되어야 한다. 이 문제의 경우, 이러한 조건을 충족하는 것을 볼 수 있다. 이제, 각각에 대하여 $n$을 계산한 뒤, $crt$를 써주면 된다.

$P_i=\frac{n}{p_i^{e_i}}$에 대하여 $P_i$의 $order$은 $p_i^{e_i}$이다. $p_i^{e_i}$는 작으므로 $discrete\_log$함수로 빠르게 구해질 것이다.

prime, exp = zip(*factor(E.order()))
dlogs = []
primes = [prime[i]^exp[i] for i in range(len(prime))]
for fac in primes:
	t = int(G.order() / fac) #E.order()로 해도 상관없음
    dlog = discrete_log(t*public, t*G, operation="+")
    dlogs.append(dlog)

이제 $dlogs$와 $p_i^{e_i}$의 $crt$로 $n$을 구하면 된다.

n = crt(dlogs, primes)

$flag$는 직접 이해한 뒤, 각자 풀어보길 바란다.