표준정규부

• 표준화:
○ z = (X - μ) / (σ / √n)

• 표준정규분포에서
○ 95% → -1.96 ≤ z ≤ 1.96

• 부등식을 μ에 대해 풀면 → 신뢰구간알 수 있음

예시)

• 측정값 X = 20
• 표준편차 σ = 5

계산:
-1.96 ≤ (20 - μ) / 5 ≤ 1.96
→ 10.2 ≤ μ ≤ 29.8

: μ가 존재할 것으로 추정되는 구간을 알 수 있다
표본으로부터 계산한 신뢰구간 안에 μ가 있을 가능성이 95%다
ㄴ뭘로??? z스코어를 가지고

z-스코어:

데이터가 평균에서 얼마나 멀리 떨어져 있는지를 '표준편차 단위'로 바꾼 값
서로 다른 단위를 공정하게 비교해주는 표준화(Z점수)

예를 들어, 신체검사에서 제 키가 평균보다 10cm 크고, 표준편차가 5cm라면 → z = 2.
즉, 평균보다 두 칸(표준편차 단위) 위에 있다는 뜻
신뢰구간은 이런 z-스코어 기준을 사용해 ‘95% 확률로 평균이 들어올 범위’를 계산

z-스코어 = "평균에서 얼마나 멀리 있는지, 표준편차 몇 칸 떨어져 있는지"
신뢰구간 = "그 기준(±1.96)을 이용해 평균(μ)의 가능 범위를 추정한 것

z-스코어 = 표준화(standardization) 라고 부르는 이유:
원래의 데이터가 가진 “위치와 단위”를 없애고 표준정규분포(평균 0, 표준편차 1)로 바꿔주기 때문
(예시) 1. 원래 데이터의 문제

시험 점수: 평균 70점, 표준편차 10점
키(cm): 평균 170, 표준편차 5
👉 두 값은 “단위도 다르고, 스케일도 달라서” 직접 비교하기 어려움

표준화(standardization) 과정

공식:

𝑧=(𝑋−𝜇)/𝜎

X − μ → 평균을 0으로 맞추기 (평균 제거 → 위치 이동)
÷ σ → 표준편차를 1로 맞추기 (흩어진 정도를 1로 맞추기 → 스케일 통일)

결과: 모든 분포가 평균 0, 표준편차 1인 분포로 변환됨 = 표준정규분포

잘못된 해석
• “이번 구간이 95% 확률로 μ 포함” 아님
• “σ 모르는 경우에도 z 사용” 아님
ㄴ> 모르면 z스토어(z = (X - μ) / (σ / √n)) 계산식을 못씀
올바른 해석:
• 절차로 만든 구간의 95%가 μ 포함
• σ 모르면 t-구간 사용

Q. t 구간이 무엇인가??(heavy tail)
z와 t의 차이

z-분포: 표준편차 σ를 알고 있다고 가정 → 정확한 기준
t-분포: σ를 모르고 s를 대신 쓰기 때문에 꼬리가 두꺼움 (불확실성 반영)

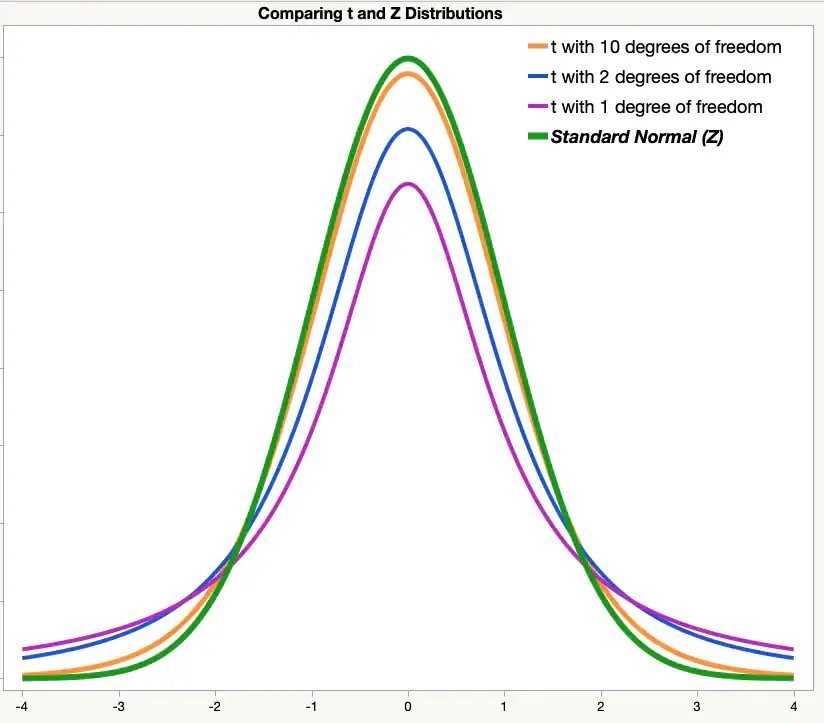
표본 수가 커질수록 s ≈ σ → t-분포는 z-분포에 수렴

큰수의 법칙과 t-분포의 꼬리가 두꺼운 이유

표본 크기가 작음 → 표본평균의 들쭉날쭉 흔들림이 큼)-> 주사위 평균 3.5 그래프 생각
같은 모집단에서 뽑아도 표본평균이 크게 벗어날 수 있음
된장국 비유
큰 국자로 떠먹으면 → 국물 맛이 평균과 거의 같음 (표본 크기 ↑ → SE ↓)
작은 국자로 떠먹으면 → 짠 부분, 싱거운 부분이 나올 수 있음 (표본 크기 ↓ → SE ↑)
그래서 표본 평균이 “평균에서 크게 벗어난 값(극단값)“이 더 자주 나타남
heavy tail 연결
극단값이 더 자주 나오니까, 분포가 정규분포보다 꼬리가 두꺼운 모양이 됨
= t-분포