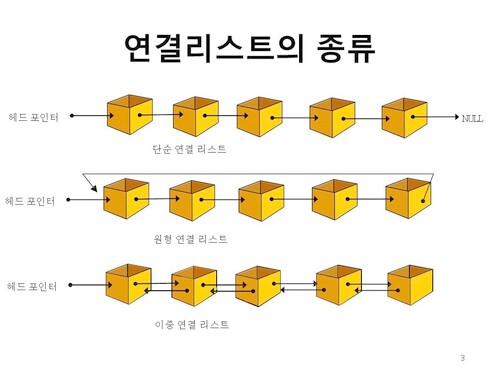
1. 단일 연결 리스트(Singly Linked List)
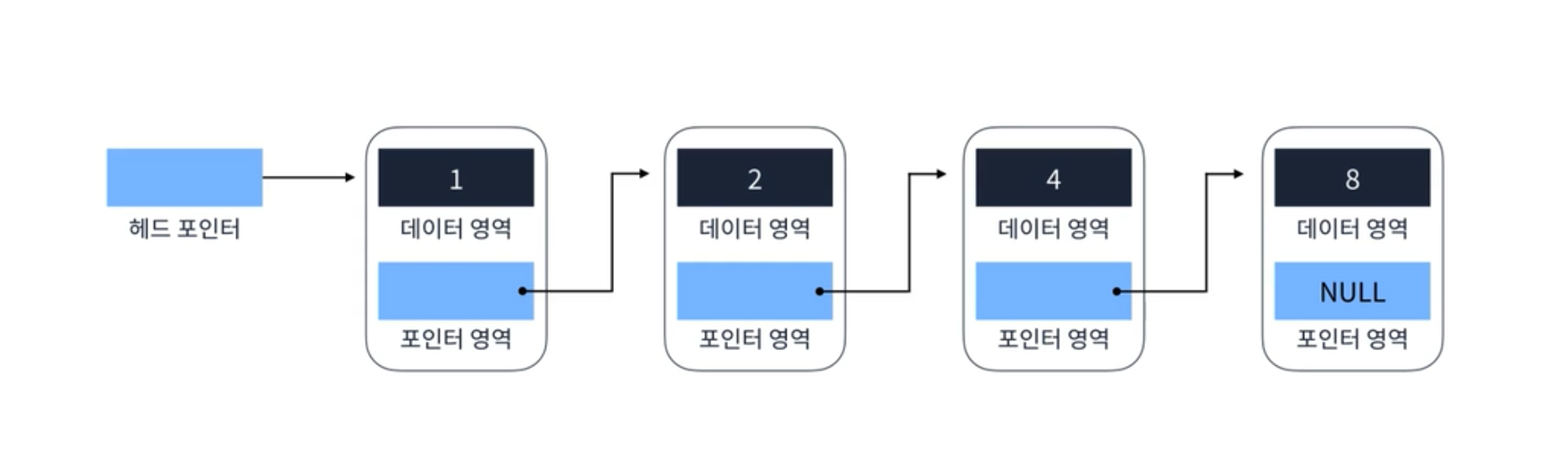
Head 에서 Tail 까지 단방향으로 이어지는 연결 리스트이며, 가장 단순한 형태인 연결 리스트이다. 여기서 Head 는 가장 첫번째 요소를 말하고 Tail 은 가장 마지막 요소를 말한다.
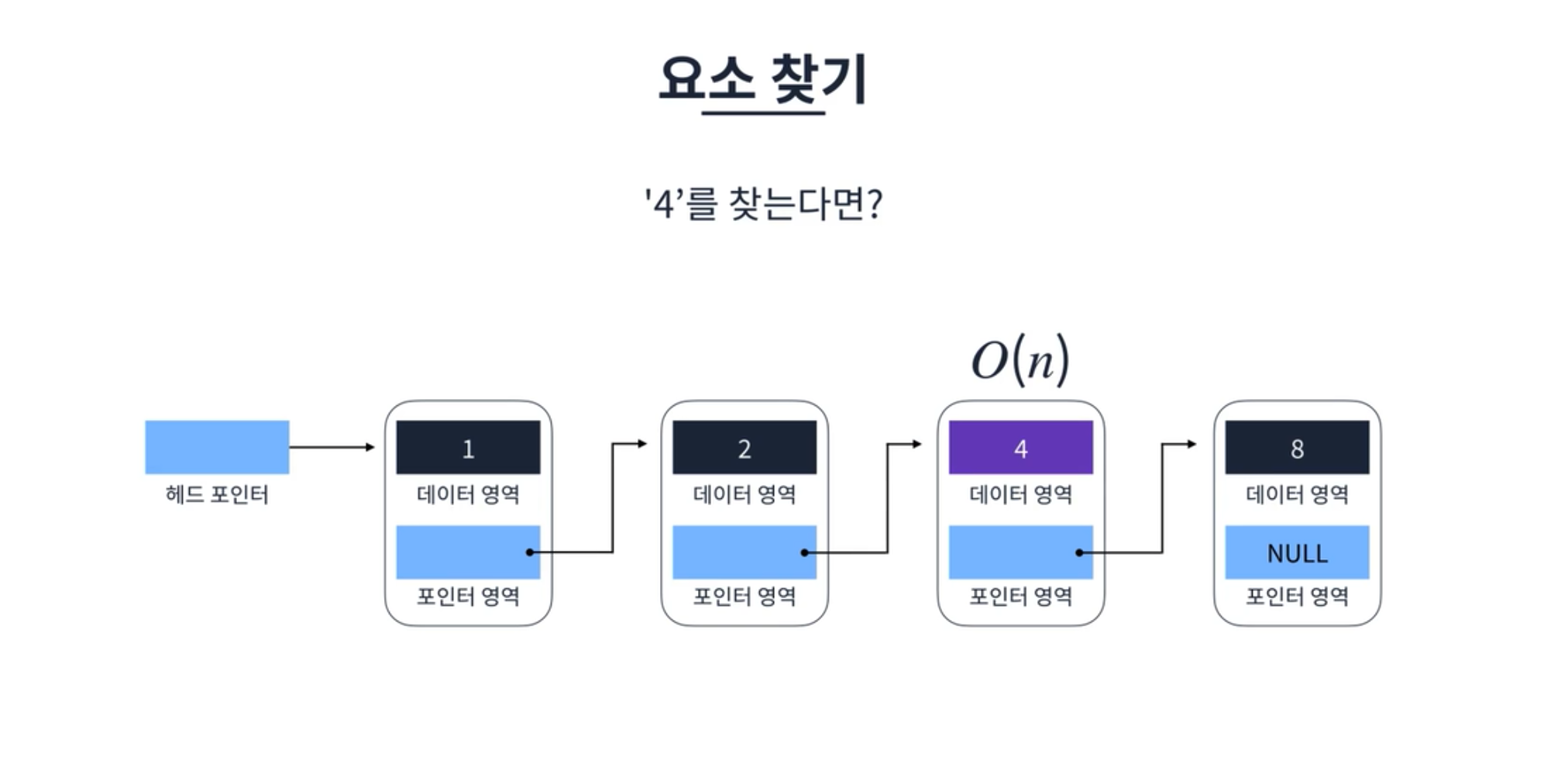
요소 찾기
요소 찾기에서 ‘4’를 찾는다고 하면 먼저 헤드 포인터에서 시작하여 각 요소의 포인터 영역을 통해 다음 요소로 넘어간다. ‘4’를 가지고 있는 요소를 찾을 때까지 이 작업을 반복하며 찾기 완료 시 로직이 종료된다. 이때, 요소 찾기의 시간 복잡도는 선형 시간 O(n) 이 소요된다.
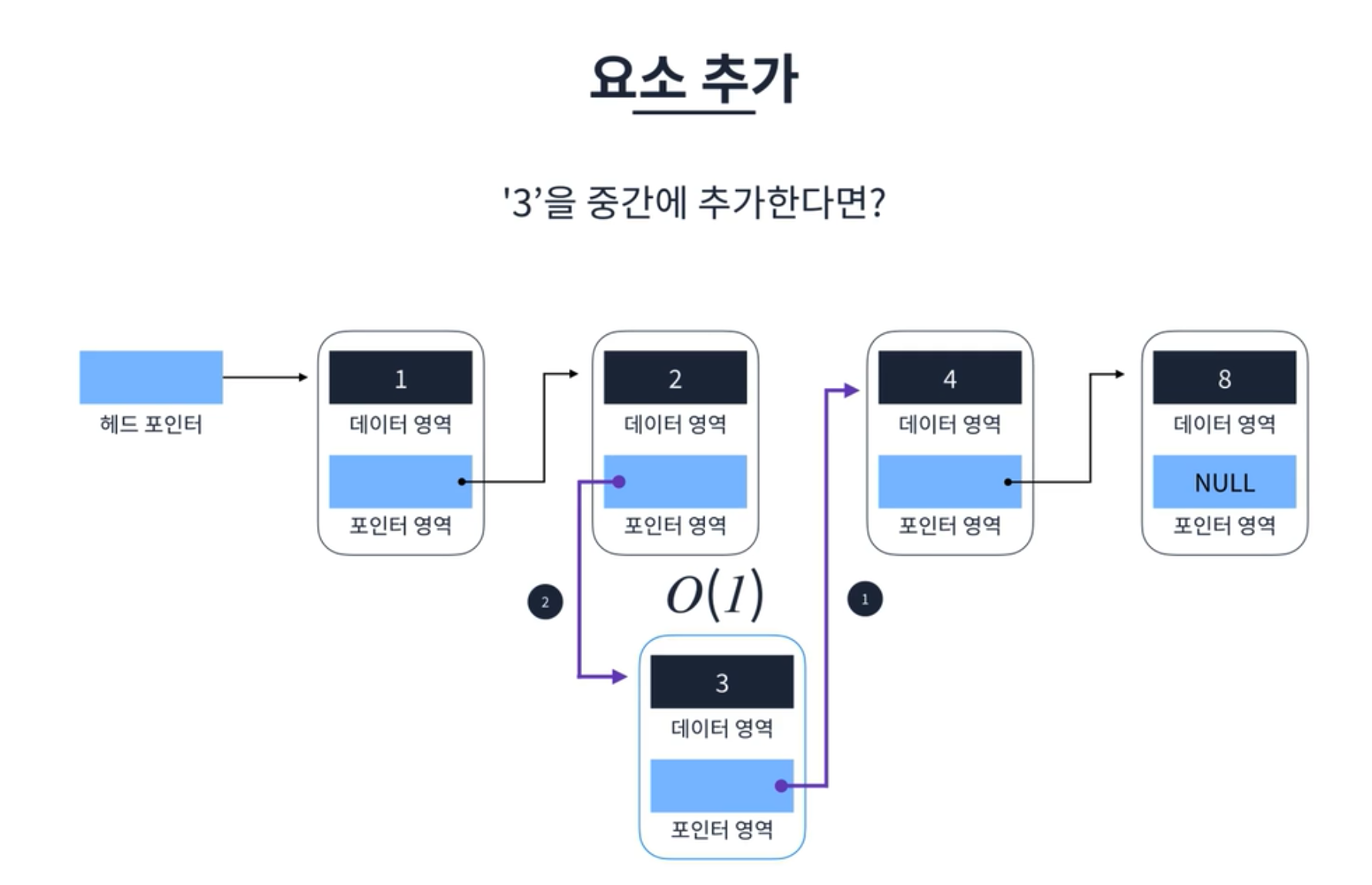
요소 추가
요소 추가에서 ‘3’을 ‘2’와 ‘4’ 사이에 추가한다면 ‘3’ 요소의 포인터를 ‘4’ 요소의 데이터 영역을 가리키게 한다. 이어서 ‘2’ 요소의 포인터를 ‘3’ 요소의 데이터 영역을 가리키게 한다. 결과적으로 굉장히 단순한 로직이기 때문에 상수 시간 O(1)이 소요된다.
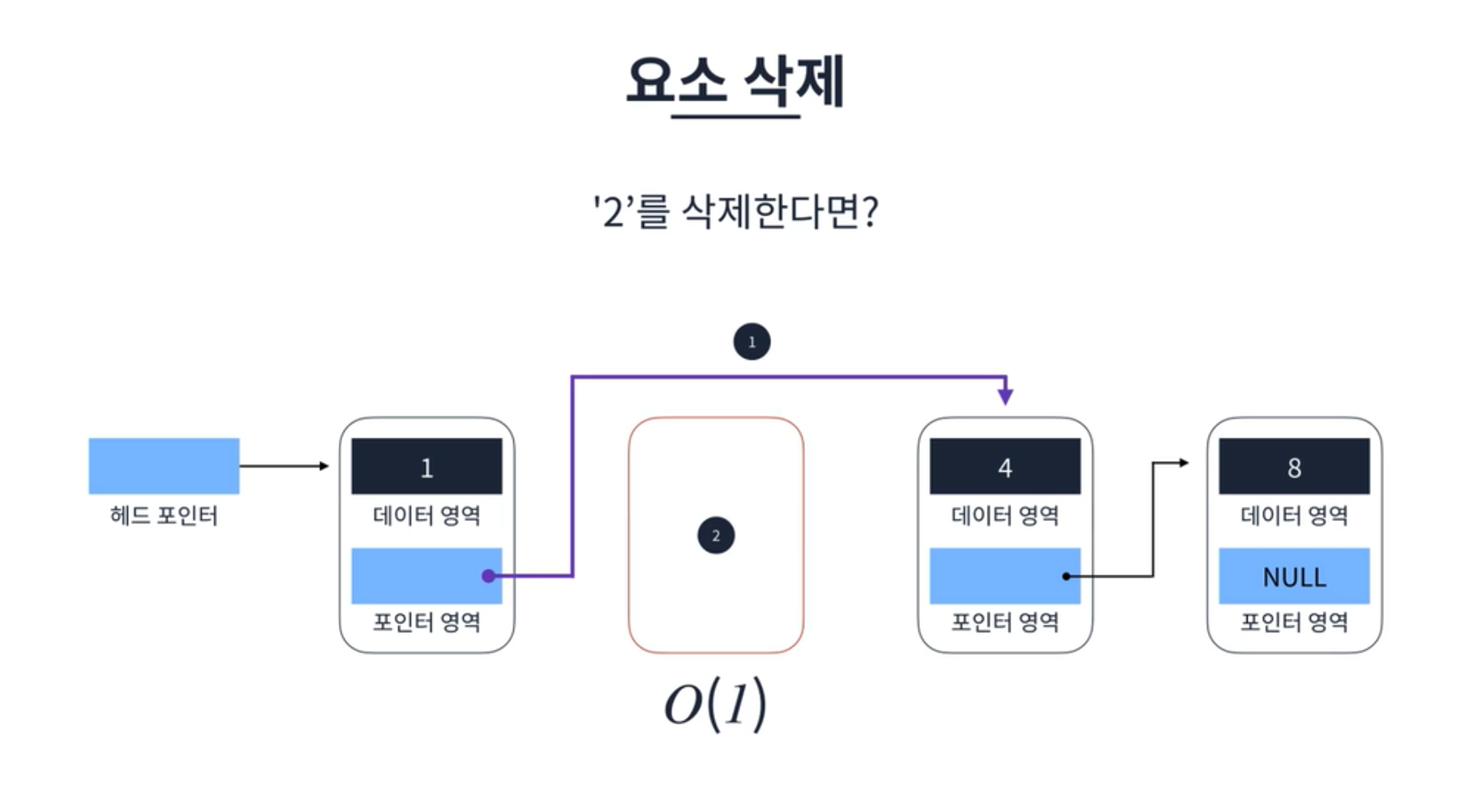
요소 삭제
요소 삭제에서 ‘2’를 삭제한다면 ‘2’ 요소 이전의 요소 포인터를 ‘2’ 요소의 포인터가 가리키는 요소로 가리키게 한다. 그리고 ‘2’ 요소를 메모리 상에서 완전히 삭제한다. 정말 어이가 없을 정도로 간단하다. 간단한 만큼 상수 시간 O(1)이 소요된다.
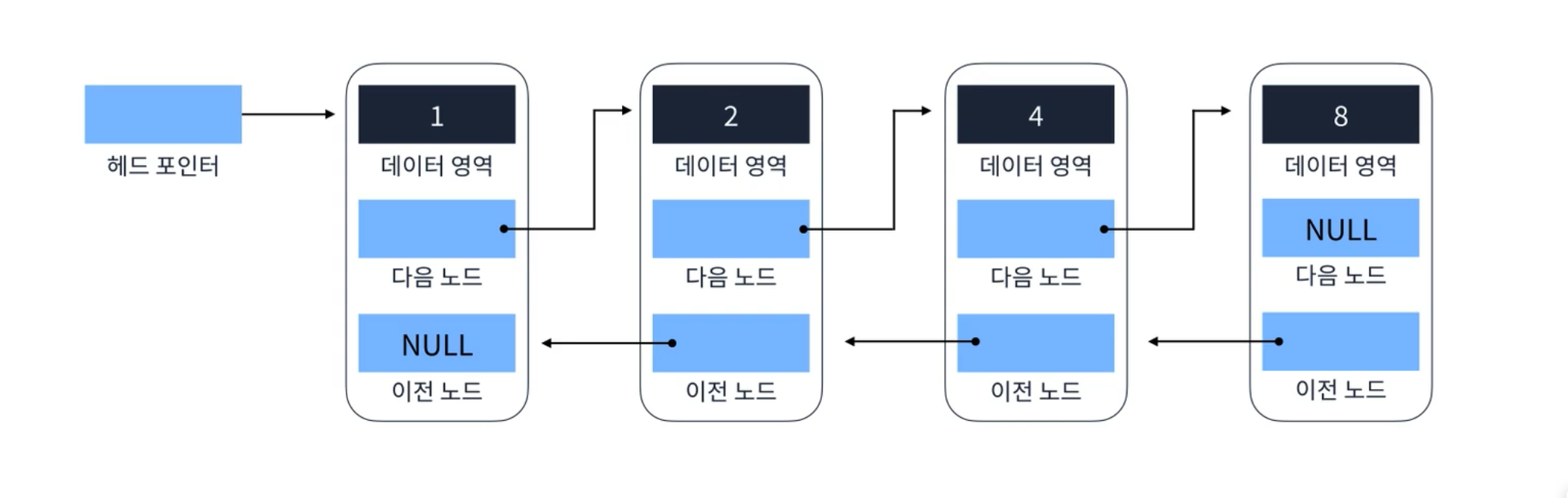
2. 이중 연결 리스트(Doubly Linked List)
양방향으로 이어지는 연결리스트로 단일 연결 리스트(Singly Linked List) 보다 자료구조의 크기가 조금 더 크다. 단인 연결 리스트와 다르게 이중 연결 리스트는 포인터가 2개 존재한다. 즉, 다음과 이전을 가리킬 수 있어 양방향으로 이어지는 구조를 가질 수 있다. 포인터 변수가 하나 더 추가 되었기 때문에 단일 연결 리스트보다 자료 구조의 크기가 조금 더 크다는 단점이 있다.
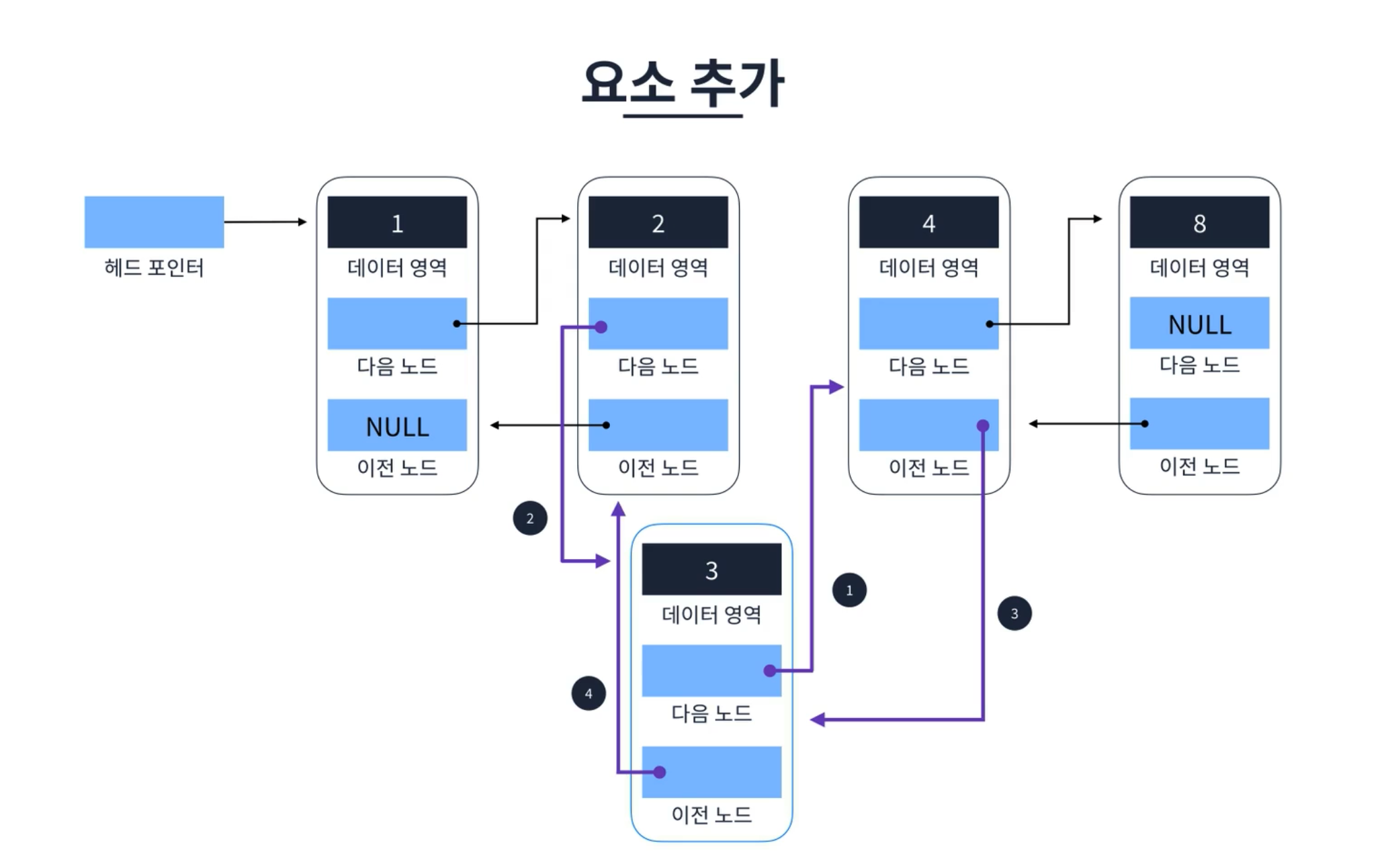
요소 추가
요소 추가에서 ‘3’ 을 ‘2’ 와 ‘4’ 사이에 추가 한다면 먼저 ‘3’ 요소의 포인터를 다음 요소인 ‘4’ 요소로 가리키도록 한다. ‘4’ 요소의 포인터를 ‘3’ 요소를 가리키도록 하고 ‘2’ 요소의 포인터를 ‘3’ 요소를 가리키도록 한다. 그리고 다시 ‘3’ 요소를 ‘2’ 요소를 가키리도록 하면 요소 추가의 로직이 종료된다. 요소 추가의 시간 복잡도는 상수 시간 O(1)이 소요된다.
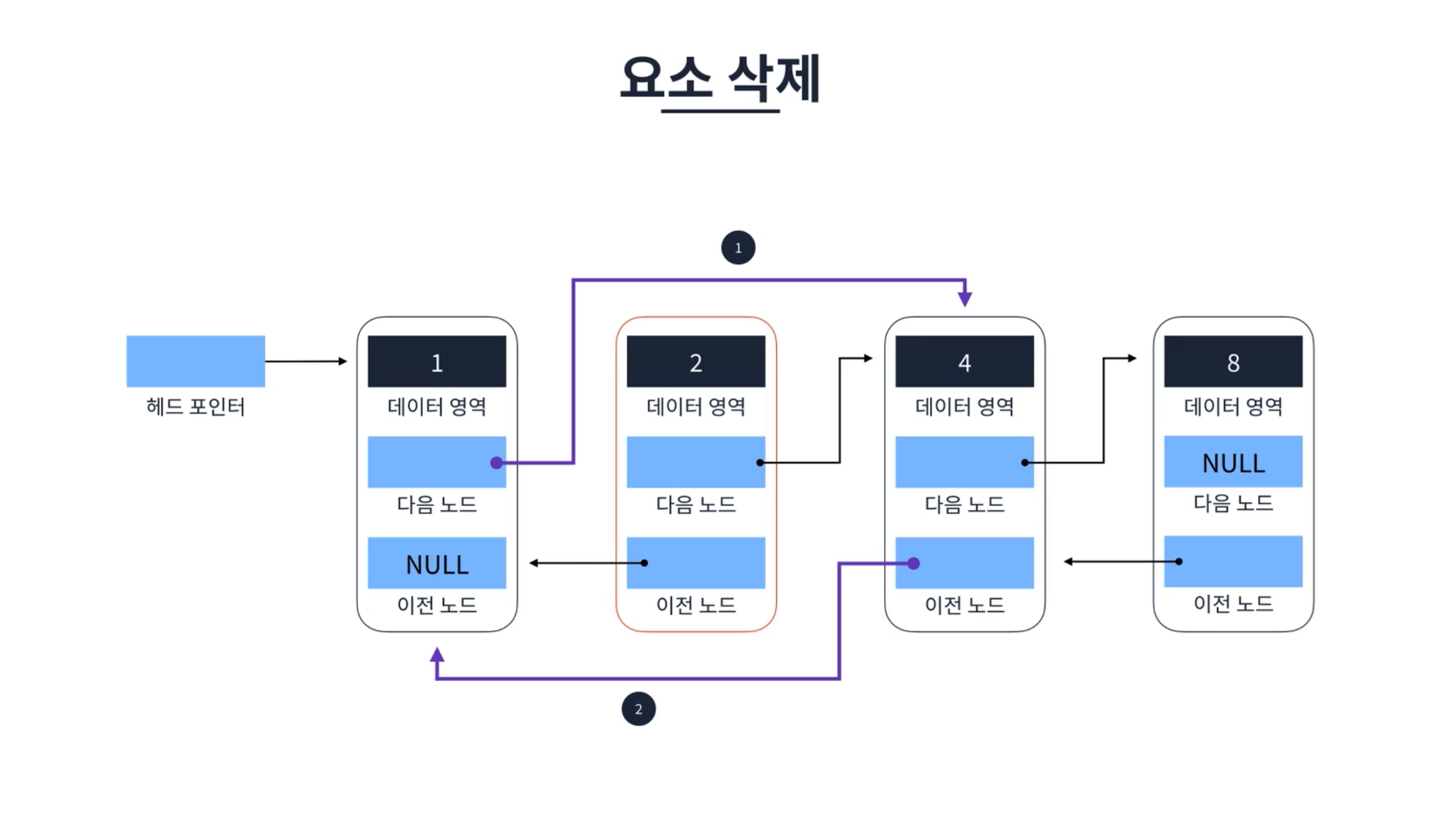
요소 삭제
요소 삭제에서 ‘2’ 요소를 삭제한다면 먼저 삭제할 요소의 이전 요소가 다음 요소로 삭제할 요소의 다음을 가리키도록 한다. 만약 단일 연결 리스트였다면 삭제 로직이 종료되었지만 이중 연결 리스트에서는 삭제할 요소의 다음 요소가 이전 요소 삭제할 요소의 이전을 가리키도록 하면 된다. 마지막으로 삭제할 요소의 메모리상에서 제거하면 삭제 로직이 종료된다. 마찬가지로 시간 복잡도는 상수 시간이 소요된다.
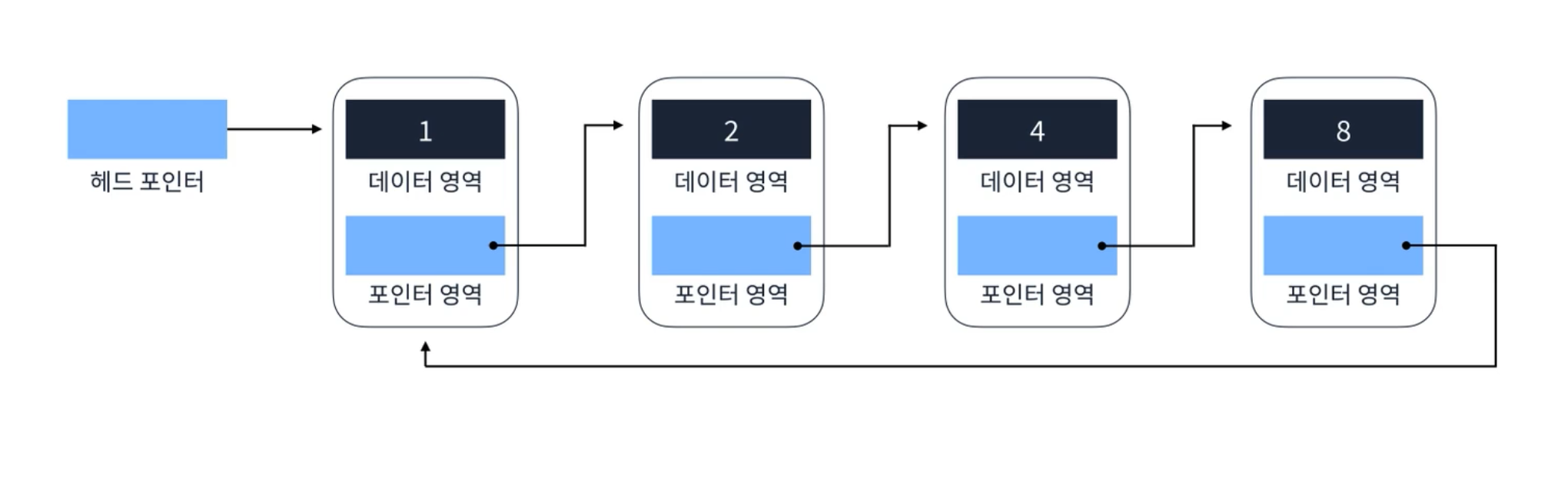
3. 환형 연결 리스트(Circular Linked List)
Singly 혹은 Doubly Linked List 에서 Tail 이 Head 로 연결되는 연결 리스트로써 메모리를 아껴 쓸 수 있다. 원형 큐 등을 만들떄도 사용된다. 사실 환형 연결 리스트는 한가지만 제외하면 단일 연결 리스트, 이중 연결 리스트와 거의 동일하다. 그렇기에 로직도 크게 다르지 않다. 한가지 다른 점은 리스트의 Tail 이 Head 로 연결 되도록 만드는 연결 리스트라는 점이다. 말 그대로, 환경으로 연결 되는 리스트이기 때문에 중간에서 탐색을 시작하더라도 한 바퀴를 전부 탐색할 수 있다.