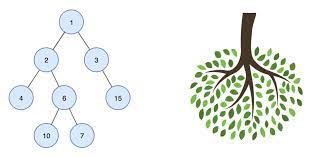
트리란?
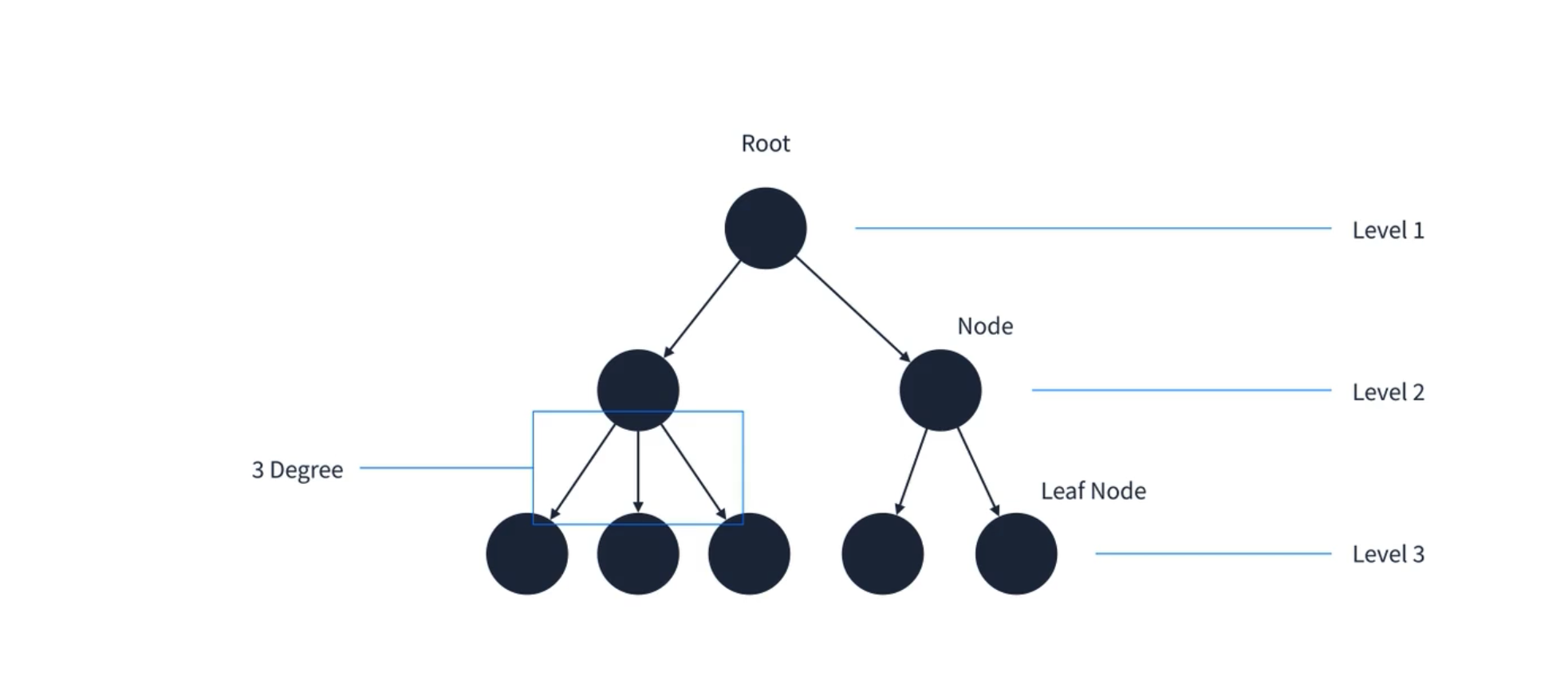
방향 그래프의 일종으로 정점을 가리키는 간선이 하나 밖에 없는 구조를 가지고 있다. 하나의 root 에서 하위로 뻗어나가는 구조를 가지고 있다. 용어 설명을 하자면 가장 상위에 존재하는 정점을 root 라고 부른다. 각 정점은 Node 라고 부르며 더 이상 자식이 없는 정점을 leaf 노드라고 부른다. 그리고 트리에는 레벨이라는 개념이 존재한다. 레벨은 root 로부터 몇 번째 깊이인지를 표현할 때 쓰인다. 그림에서 표현한 트리는 레벨3까지 존재한다.
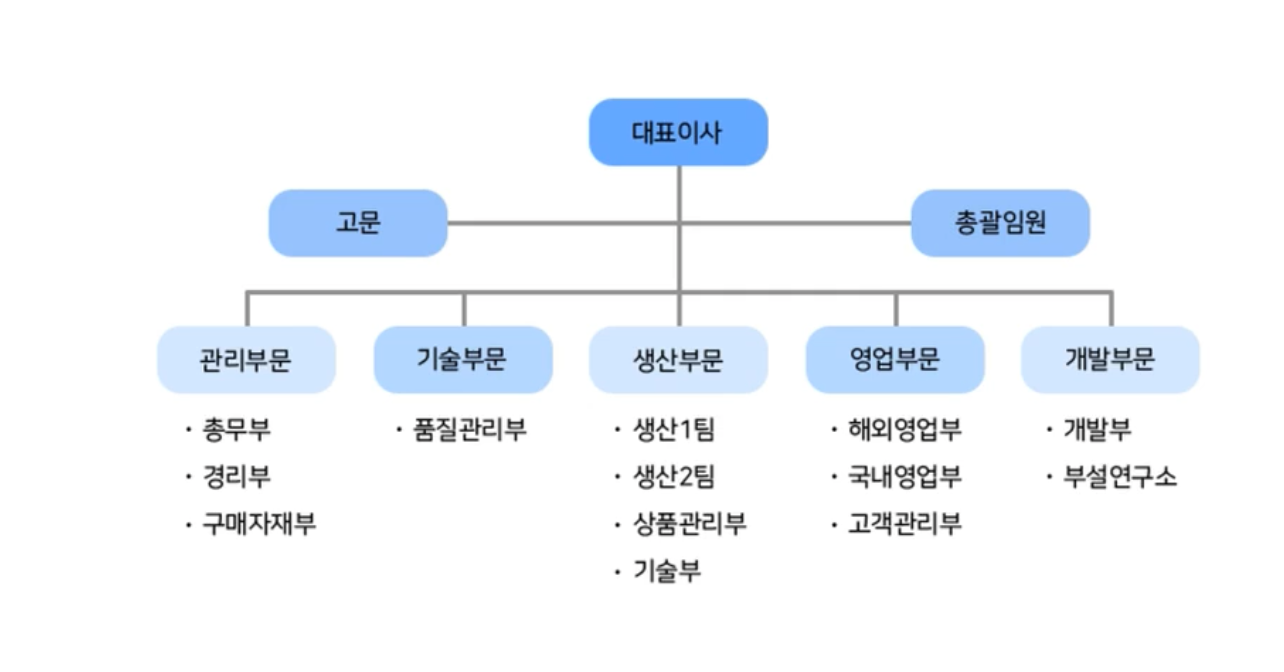
그리고 한 정점에서 뻗어나가는 정점 수를 Degree 혹은 차수라고 부른다. 이런 트리는 어디에서 많이 사용할까? 가장 먼저 사용되는 곳은 조직도이다. 아래의 그림을 보면 대표이사부터 시작하여 여러 부서로 뻗어나가고 있다. 위의 그림처럼 트리의 특징과 비슷하다.
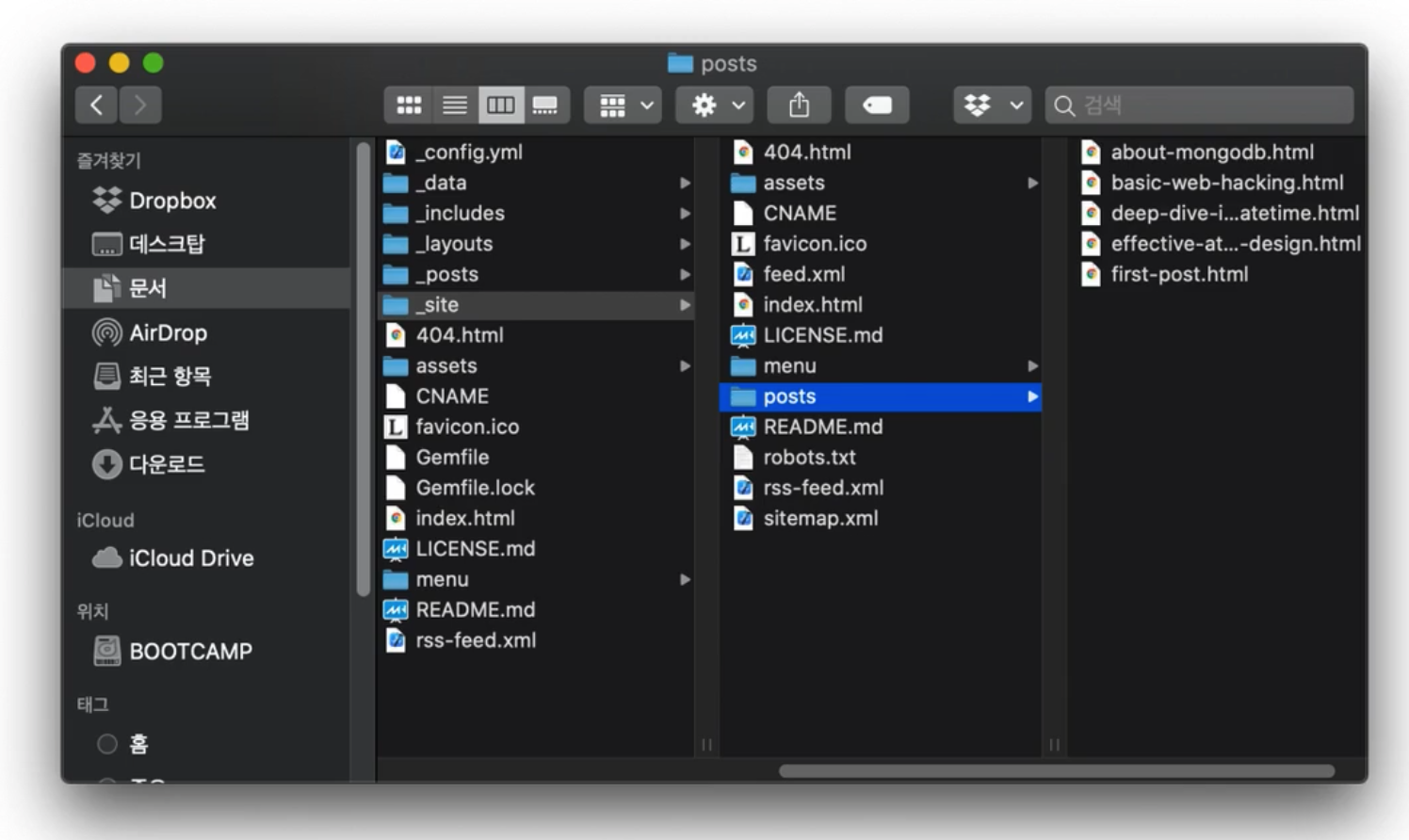
그리고 소프트웨어에서 떠올릴 수 있는 것은 디렉토리 구조이다. 이처럼 트리도 다양한 곳에서 쓰일 수 있는 자료구조이다.
트리의 특징
- 루트 정점을 제외한 모든 정점은 반드시 하나의 부모 정점을 가진다.
- 정점이 N개인 트리는 반드시 N-1개의 간선을 가진다. 왜냐하면 하나의 부모 정점만을 가지기 때문이다.
- 루트에서 특정 정점으로 가는 경로는 유일하다.
이진 트리
이진 트리란?
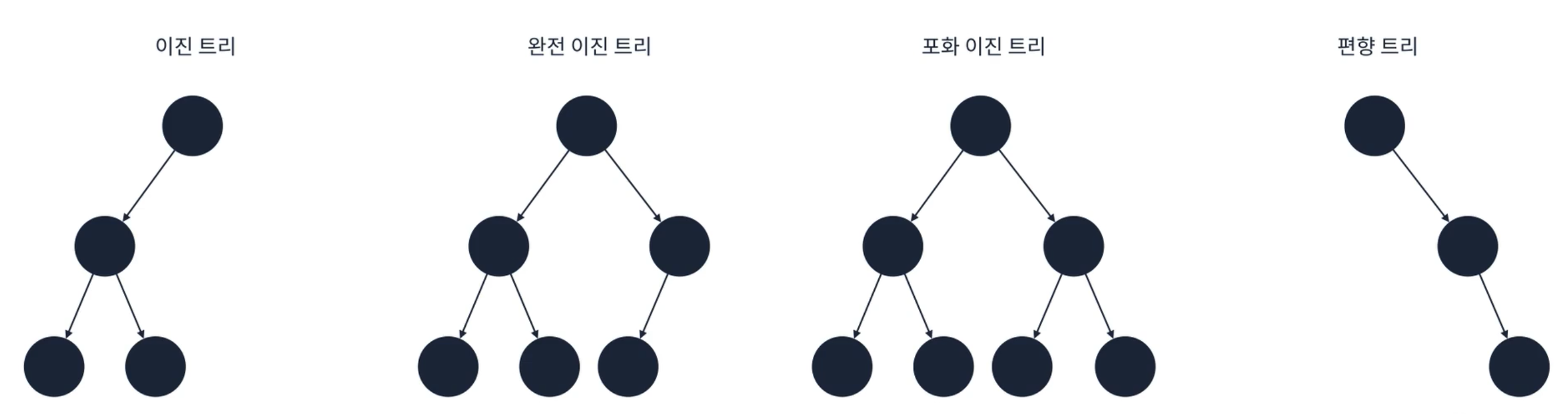
이진 트리는 각 정점이 최대 2개의 자식을 가지는 트리를 의미한다.탐색을 위한 알고리즘에서 많이 사용되므로 그 특징을 알아두면 좋다.완전 이진 트리는 마지막 레벨을 제외하고 모든 정점이 채워져 있는 트리를 의미한다. 만약 마지막 레벨도 모두 채워져 있다면 포화 이진 트리라고 부른다. 편향 트리의 경우에는 한 방향으로만 정점이 이어져 있는 것을 뜻한다.
이진 트리의 특징
- 정점이 N개인 이진 트리는 최악의 경우 높이가 N이 될 수 있다. N개의 정점을 가진 편향 트리가 된다고 생각하면 된다.
- 정점이 N개인 포화 또는 완전 이진 트리의 높이는 logN 이다. 레벨이 증가 됨에 따라 2배씩 정점이 생기기 때문이다.
- 높이가 h인 포화 이진 트리는 2의 h제곱 - 1개의 정점을 가진다. 이진법을 생각하면 편하다.
- 일반적인 이진 트리를 사용하는 경우는 많지 않다. 다음 자료구조에 응용된다. -> 이진 탐색 트리, 힙, AVL 트리, 레드 블래 트리
트리의 구현 방법
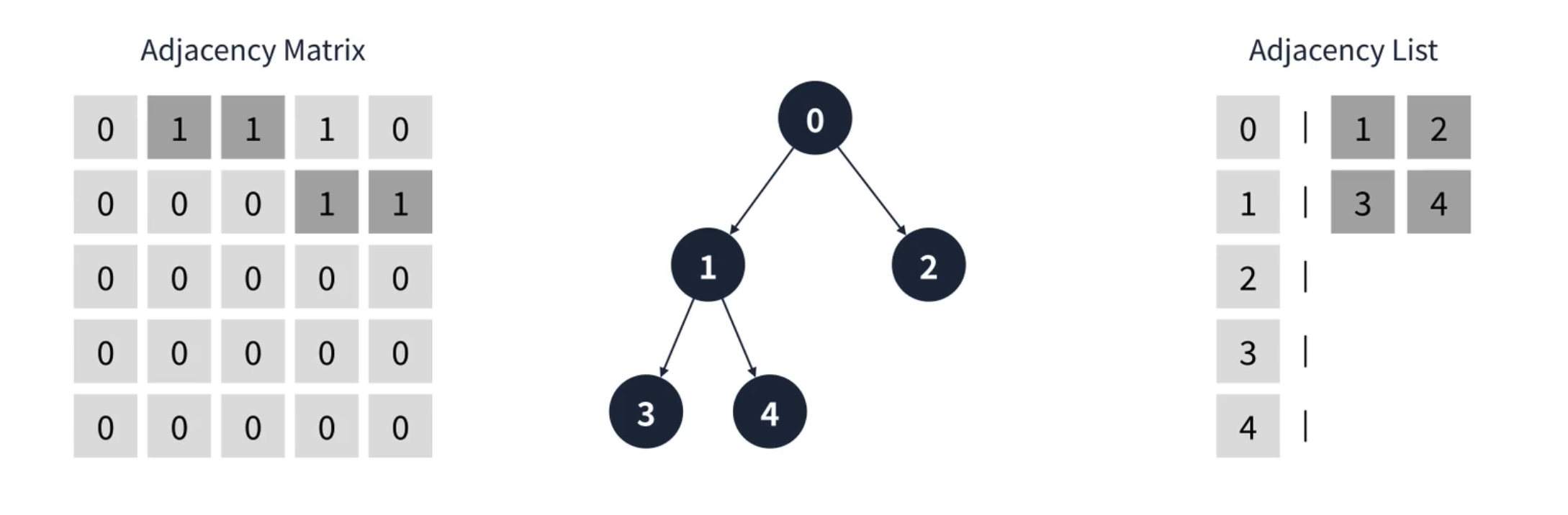
트리가 그래프의 일종인 만큼 트리의 구현 방법도 그래프와 동일하게 인접 행렬 리스트 두가지 방식으로 트리를 표현할 수 있다.
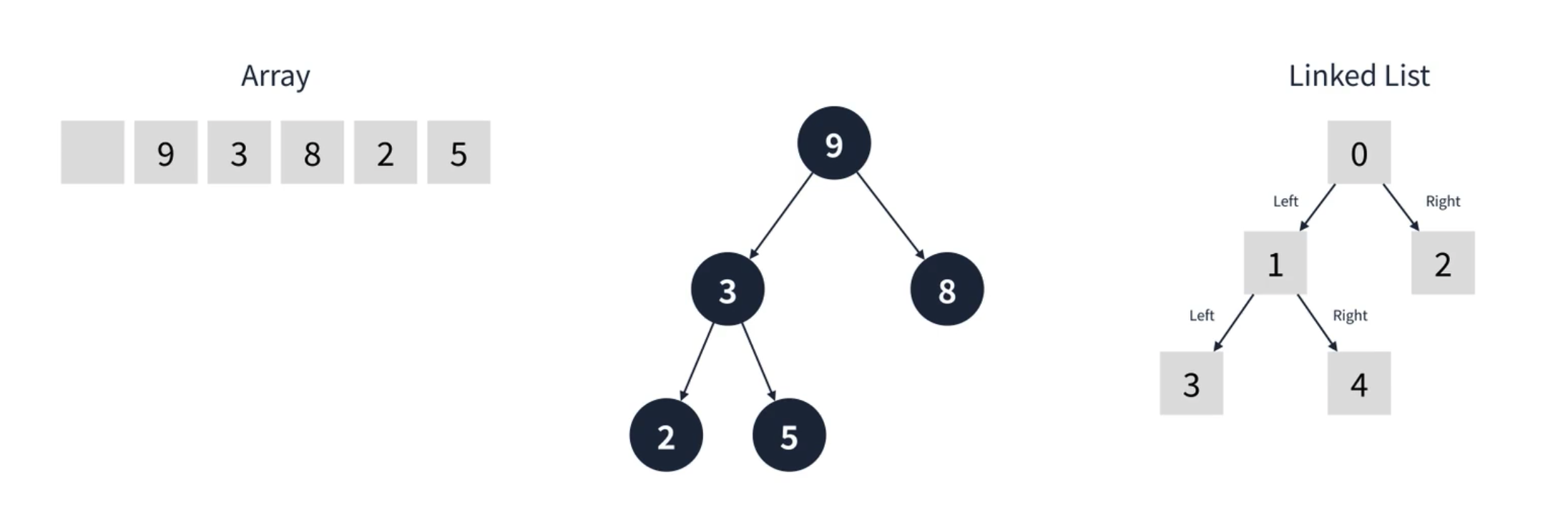
이진 트리의 경우 자식의 수가 2개 이하로 제한 되는 특징 때문에 조금 더 최적화된 방식으로 구현이 가능하다. 1차원 배열 혹은 링크가 두개 존재하는 연결 리스트로 구현이 가능하다.
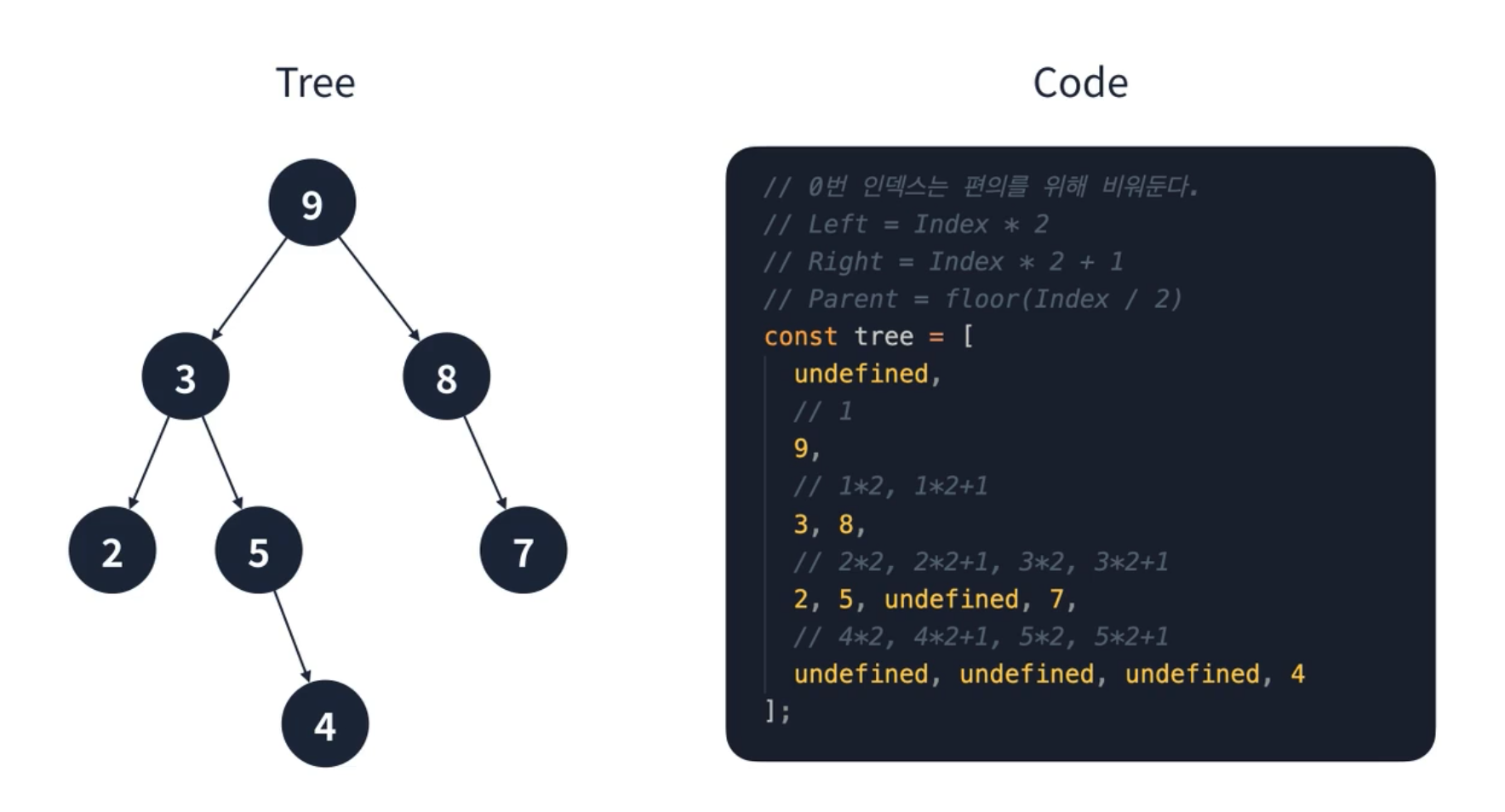
JavaScript 에서 이진 트리의 구현 방법은 배열을 사용하면 된다. 단, 몇가지 규칙을 지켜야 한다. index 2 를 하면 왼쪽 정점이고 index 2 + 1 을 하면 오른쪽 정점이 된다. 만야 부모 정점을 알고 싶다면 Index / 2 로 나누고 소수점을 버리면 된다. 이런 방식으로 굉장히 간단하게 이진 트리를 표현할 수 있다.
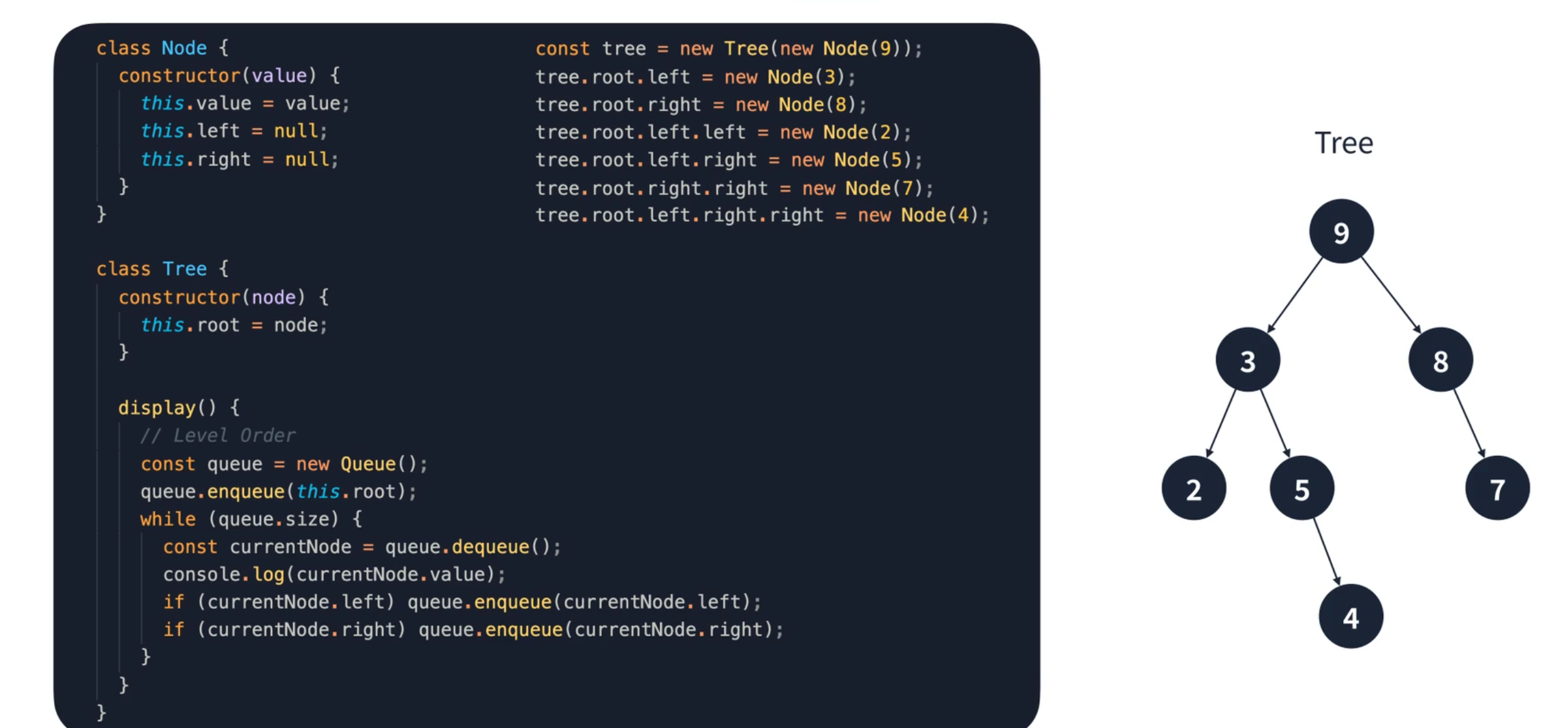
이진 트리를 연결 리스트로 구현하는 것도 그렇게 어렵지는 않다. 기존 연결리스트의 노드에 next 대신 left 와 right 를 넣는다. 그리고 계속 left 와 right 에 값을 연결 시켜주면 이진 트리가 완성된다.