요세푸스 문제는 다음과 같다.

1번부터 N번까지 N명의 사람이 원을 이루면서 앉아있고, 양의 정수 K(≤ N)가 주어진다. 이제 순서대로 K번째 사람을 제거한다. 한 사람이 제거되면 남은 사람들로 이루어진 원을 따라 이 과정을 계속해 나간다. 이 과정은 N명의 사람이 모두 제거될 때까지 계속된다. 원에서 사람들이 제거되는 순서를 (N, K)-요세푸스 순열이라고 한다. 예를 들어 (7, 3)-요세푸스 순열은 <3, 6, 2, 7, 5, 1, 4>이다.

N과 K가 주어지면 (N, K)-요세푸스 순열을 구하는 프로그램을 작성하시오.

---

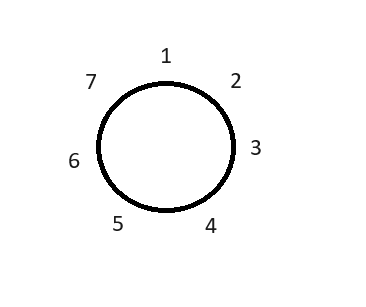
그림과 같이 1~7명의 사람들이 있다고 하면 첫번째에 3번째인 3번 사람이 제거 되고, 그이후 3번째사람인 6번이 제거되고 그다음은 2,7,5,1,4순으로 제거가 되어야한다.
queue를 활용하는 문제이기에 queue의 특성인 FIFO특성을 잘 활용할 필요가 있었다.

FIFO(First in First Out)

queue는 stack과 달리 먼저 넣은것이 먼저나온다는 선입선출의 특성을 가지고 있기에
pop()을 사용하면 마지막에 넣은것이 아닌 먼저넣은것이 제거가 된다.

밑의 그림은 선입선출 개념을 돕기 위한 터널 속 기차 이미지로 기차의 머리가 터널에 먼저 들어가니 터널 밖으로 기차머리가 먼저 빠져나온다.

핵심코드는 아래 코드이다.

while (!people.empty())
{
	for (int i = 0; i < K-1; i++) 
	{
		people.push(people.front()); //첫번째와 두번째 원소는 PUSH를 통해 뒤로 보내준다.
		people.pop(); //뒤로 보내줄때마다 제거해줌.
	}
	arr[count++] = people.front(); //배열을 통해 3번째원소를 넣어줌 
	people.pop(); //3번째 원소 제거 
} 

queue의 front와 pop을 활용해 첫번째 두번째 원소를 queue의 뒤로 보내준다.
이후 세번째 원소를 배열에 넣어주고 제거한다.
위 방식을 queue안에 원소가 없어질때까지 while문을 돌려 반복해준다.

전체코드

#include<iostream>
#include<queue>
using namespace std;
int arr[1001]; // (1 ≤ K ≤ N ≤ 1,000)

int main()
{
	queue<int>people;
	
	int N, K;
	cin >> N >> K;
	for (int i = 1; i <= N; i++)
	{
		people.push(i);
	}
	int count = 0;
	while (!people.empty())
	{
		for (int i = 0; i < K-1; i++)
		{
			people.push(people.front()); 
			people.pop();
		}
		arr[count++] = people.front();
		people.pop();
	}
	cout << "<";
	for (int i = 0; i < count; i++)
	{
		if (i == count - 1)
		{
			cout << arr[i] << ">";
		}
		else
		{
			cout << arr[i] << ", ";
		}
	}

	return 0;
}

채점결과