AVL 트리를 다루었을때 Delete 부분은 시간이 걸릴것같아 삽입과정 및 Rotate 를 다루는 코드만 제작을하였다
이번에는 그 코드에서 Delete가 추가 되었다

구현 코드

#include<iostream>
using namespace std;

template<typename T>
class AVLTree
{
private:
    struct Node
    {
        int height;
        T data;
        Node* left;
        Node* right;

        Node(T value)
        {
            data = value;
            height = 1;
            left = nullptr;
            right = nullptr;
        }
    };
    Node* root;

public:
    AVLTree() : root(nullptr) {}

    void Insert(T data)
    {
        root = Inserting(root, data);
    }
    void Delete(T data)
    {
        root = DeleteNode(root, data);
    }
    void Print()
    {
        InOrder(root);
        cout << '\n';
    }
  private:
   int Height(Node* node)
   {
       if (!node)return 0;
       return node->height;
   }

   int BalanceFactor(Node* node)
   {
       if (!node)return 0;
       else return Height(node->left) - Height(node->right);

   }

   Node* Inserting(Node* node, T data)
   {
       if (!node)return new Node(data);

       if (data < node->data)
       {
           node->left = Inserting(node->left, data);
       }
       else if (data > node->data)
       {
           node->right = Inserting(node->right, data);
       }
       else return node; //중복데이터는 방지

       node->height = 1 + max(Height(node->left), Height(node->right));

       return Rebalance(node);
   }
   Node* DeleteNode(Node* node, T data)
   {
       if (!node)
       {
           cout << "해당 데이터 없음" << '\n';
           return node;
       }

       if (data < node->data)
       {
           node->left = DeleteNode(node->left, data);
       }
       else if (data > node->data)
       {
           node->right = DeleteNode(node->right, data);
       }
       else
       {

           if (!node->left || !node->right)
           {
               Node* temp = nullptr;

               if (node->left)
               {
                   temp = node->left;
               }
               else if (node->right)
               {
                   temp = node->right;
               }

               if (!temp)
               {
                   temp = node;
                   node = nullptr;
               }
               else
               {
                   node = temp;
               }
               delete temp;
           }
           else
           {
               Node* temp = FindMin(node->right);
               node->data = temp->data;
               node->right = DeleteNode(node->right, temp->data);
           }
       }
       if (!node)return node;
       node->height = 1 + max(Height(node->left), Height(node->right));

       return Rebalance(node);
   }
   Node* FindMin(Node* node)
   {
       Node* currentNode = node;
       if (!node)return node;
       while (currentNode && currentNode->left)
       {
           currentNode = currentNode->left;
       }
       return currentNode;
   }
   Node* Rebalance(Node* node)
   {
       int factor = BalanceFactor(node);

       if (factor > 1) //왼쪽으로 치우침
       {
           if (BalanceFactor(node->left) >= 0)
           {
               return LLRotate(node);
           }
           else // LR 상태
           {
               node->left = RRRotate(node->left);
               return LLRotate(node);
           }
       }
       else if (factor < -1) //오른쪽으로 치우침
       {
           if (BalanceFactor(node->right) <= 0) // RR 상태
           {
               return RRRotate(node);
           }
           else // RL 상태
           {
               node->right = LLRotate(node->right);
               return RRRotate(node);
           }
       }

       return node;
   }

   Node* LLRotate(Node* node)
   {
       Node* newNode = node->left;
       node->left = newNode->right;
       newNode->right = node;

       node->height = 1 + max(Height(node->left), Height(node->right));
       newNode->height = 1 + max(Height(newNode->left), Height(newNode->right));

       return newNode;
   }

   Node* RRRotate(Node* node)
   {
       Node* newNode = node->right;
       node->right = newNode->left;
       newNode->left = node;

       node->height = 1 + max(Height(node->left), Height(node->right));
       newNode->height = 1 + max(Height(newNode->left), Height(newNode->right));

       return newNode;
   }
   void InOrder(Node* node)
   {
       if (!node) return;
       InOrder(node->left);
       cout << node->data << " ";
       InOrder(node->right);
   }
};

int main()
{
    AVLTree<int> avl;
    avl.Insert(5);
    avl.Print();

    avl.Insert(6);
    avl.Print();

    avl.Insert(3);
    avl.Print();

    avl.Insert(7);
    avl.Print();

    avl.Insert(8);
    avl.Print();

    avl.Delete(6);
    avl.Print();

    avl.Delete(8);
    avl.Print();

    avl.Insert(11);
    avl.Print();

    return 0;
} 

굳이 int main에서 다루지 않아도 되는 부분 rotate, inserting, inorder 등은 private로 넘겼다
이번에 추가된 내용만 보도록하자

Delete

public

void Delete(T data)
{
    root = DeleteNode(root, data);
}

node를 DeleteNode 를 한후를 갱신하는것이기에 public 부분은 딱히 다룰게없다

private

Node* DeleteNode(Node* node, T data)
{
    if (!node)
    {
        cout << "해당 데이터 없음" << '\n';
        return node;
    }

    if (data < node->data)
    {
        node->left = DeleteNode(node->left, data);
    }
    else if (data > node->data)
    {
        node->right = DeleteNode(node->right, data);
    }
    else
    {

        if (!node->left || !node->right)
        {
            Node* temp = nullptr;

            if (node->left)
            {
                temp = node->left;
            }
            else if (node->right)
            {
                temp = node->right;
            }

            if (!temp)
            {
                temp = node;
                node = nullptr;
            }
            else
            {
                node = temp;
            }
            delete temp;
        }
        else
        {
            Node* temp = FindMin(node->right);
            node->data = temp->data;
            node->right = DeleteNode(node->right, temp->data);
        }
    }
    if (!node)return node;
    node->height = 1 + max(Height(node->left), Height(node->right));

    return Rebalance(node);
}
Node* FindMin(Node* node)
{
    Node* currentNode = node;
    if (!node)return node;
    while (currentNode && currentNode->left)
    {
        currentNode = currentNode->left;
    }
    return currentNode;
}

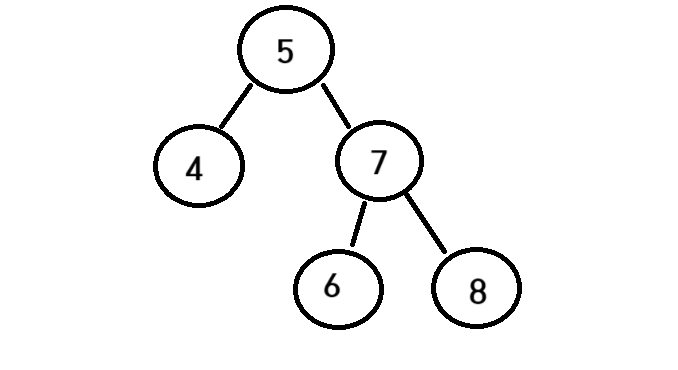
이렇게 만들어진 AVL 트리가 있다고 하자
나는 현재 7노드를 삭제시켜주고 싶다
트리가 유지 되기 위해서는 부모노드의 왼쪽 자식은 부모노드보다 작아야하고 부모노드의 오른쪽 자식은 부모노드보다 커야한다는 것이 유지가 되면서 높이 균형역시 -1~1로 유지가 되어야한다

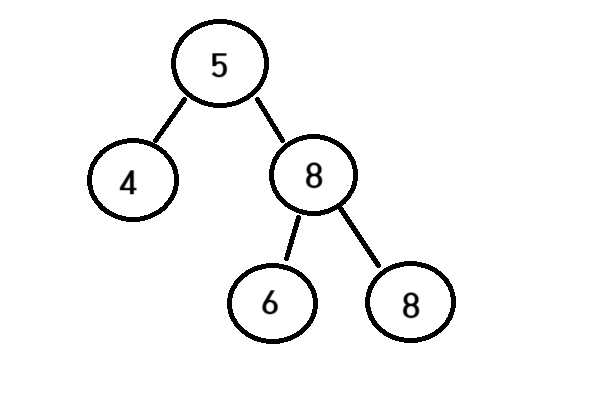
7노드의 데이터 7을 본인의 바로큰노드인 8로 값을 바꿔준다
이렇게 되면 8이 중복이된다
그렇기에
node->right = DeleteNode(node->right, temp->data);
현재 8(구 7 노드)->right를 재귀를 통해 DelteNode로 들어가준다

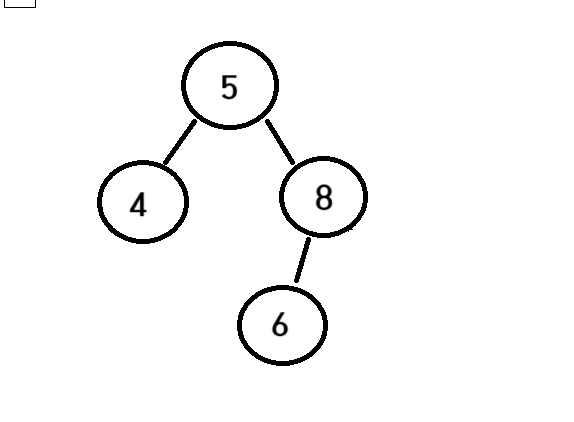
이후 중복된 8을 발견하면 삭제해주면 된다

지금 위 이미지는 삭제가 되더라도 균형이 안깨지기에 비교적 쉽다
균형이 깨지는경우는 다시 균형을 유지시키도록 해야한다

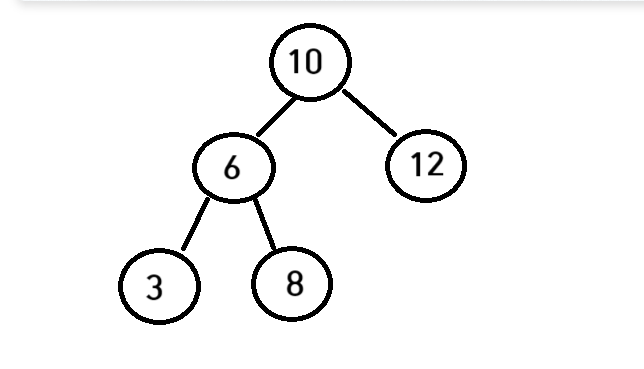
이렇게 그림이있고 나는 12를 삭제해줄거다

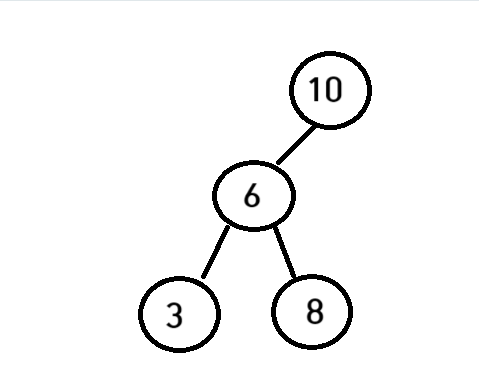
이렇게 되면 LL유형이된다

Node* LLRotate(Node* node)
   {
       Node* newNode = node->left;
       node->left = newNode->right;
       newNode->right = node;

       node->height = 1 + max(Height(node->left), Height(node->right));
       newNode->height = 1 + max(Height(newNode->left), Height(newNode->right));

       return newNode;
   }

위의 LLRotate에서 newNode 는 6이다
node->left = newNode->right
10의 left 는 6의 오른쪽인 8이된다
newNode->right =node;
6의 right 는 10이 된다
이후 높이를 조정해주고
6이 root인 newNode를 반환해주게 된다

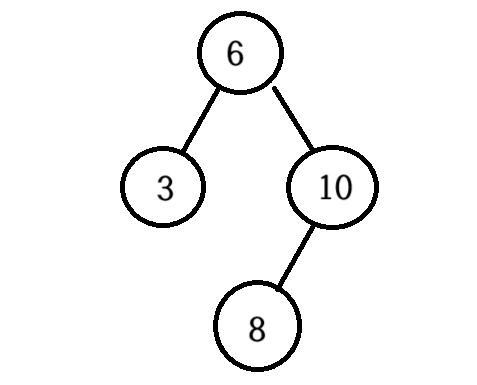
이렇게 균형을 유지할수 있게된다.

이렇게 AVL트리의 balance facotr ,ROTATE ,삽입 ,삭제를 다루어보았는데 이러한 자료구조를 다룰때 코드가 길어지다 보니 가독성이 조금씩 떨어져 일부가 틀렸을수도 있다 이후에는 #region 등으로 가독성을 올리면서 코드를 다루어야할것같다