이전에 이진 탐색트리를 알아보았다
이진탐색트리의 경우 시간복잡도가 O(logn)이긴 하지만 삽입과 삭제가 빈번히 이루어져 편향이진트리가 만들어지는경우 시간복잡도가 O(n) 이 되버리게 된다
AVL 트리
AVL 트리는 스스로 균형을 잡는 이진 탐색트리이다
한쪽을 치우친 편향이진트리처럼 트리의 높이가 높아지는 경우를 방지하고자 높이 균형을 유지하기 위해 AVL 트리를 사용할수가 있따
특징
- 왼쪽 오른쪽 서브트리의 높이 차이가 최대 1이다
- 삭제나 삽입이 일어나게되어 높이 차이가 1보다 커지게 되면 ROTATION을 통해 균형을 잡아 높이 차이를 줄인다
- AVL 트리의 시간복잡도는 O(logn)이다
Balance Factor(BF)
Balance Factor 는 AVL 트리에서 중요한 요소이며 왼쪽 서브트리 높이에서 오른쪽 서브트리의 높이를 뺀 값이다
BF= 1 : 왼쪽 서브트리의 높이가 오른쪽 서브트리의 높이보다 한 단계 높음
BF= 0: 서브트리의 높이 = 오른쪽 서브트리의 높이
BF=-1 왼쪽 서브트리의 높이 가 오른쪽 서브트리의 높이보다 한단계 낮다
불균형
불균형 유형은 다음과같다
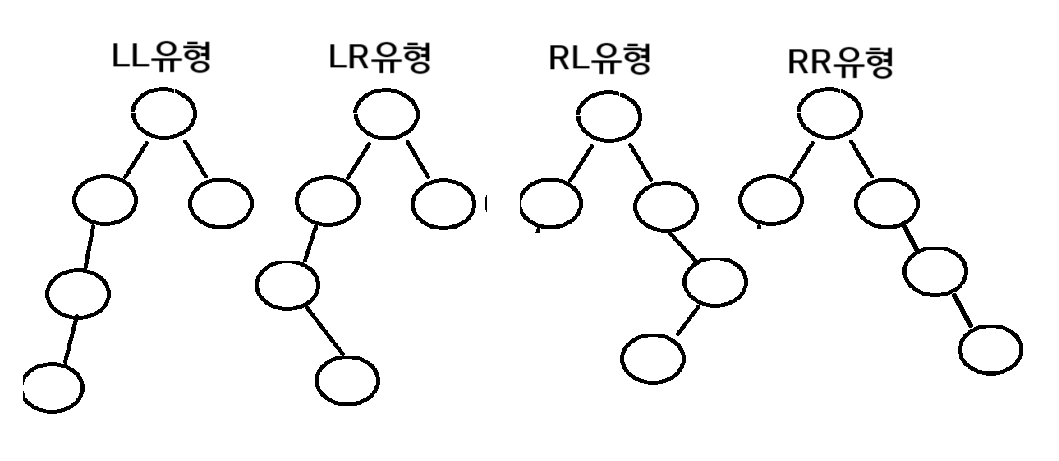
LL유형 : 불균형 발생노드의 왼쪽 자식 노드와 자식의 왼쪽 노드에 의해 왼쪽으로 기울어져있음
RR유형 : 불균형 발생 노드의 오른쪽 자식 노드와 자식의 오른쪽 자식 노드에 의해 오른쪽으로 기울어져 있음
LR유형 : 불균형 발생노드의 왼쪽 자식노드와 오른쪽 자식노드에 의해 왼쪽 서브트리가 기울어져있음
RL유형 : 불균형 발생노드의 오른쪽 자식노드와 자식의 왼쪽 자식노드에 의해 오른쪽 서브트리가 기울어져있음
구현 코드
#include<iostream>
using namespace std;
template<typename T>
class AVLTree
{
private:
struct Node
{
int height;
T data;
Node* left;
Node* right;
Node(T value)
{
data = value;
height = 1;
left = nullptr;
right = nullptr;
}
};
Node* root;
public:
AVLTree() : root(nullptr) {}
int Height(Node* node)
{
if (!node)return 0;
return node->height;
}
int BalanceFactor(Node* node)
{
if (!node)return 0;
else return Height(node->left) - Height(node->right);
}
Node* Inserting(Node* node, T data)
{
if (!node)return new Node(data);
if (data < node->data)
{
node->left = Inserting(node->left, data);
}
else if (data > node->data)
{
node->right = Inserting(node->right, data);
}
else return node; //중복데이터는 방지
node->height = 1 + max(Height(node->left), Height(node->right));
return Rebalance(node);
}
void Insert(T data)
{
root = Inserting(root, data);
}
Node* Rebalance(Node* node)
{
int factor = BalanceFactor(node);
if (factor > 1) //왼쪽으로 치우침
{
if (BalanceFactor(node->left) >= 0)
{
return LLRotate(node);
}
else // LR 상태
{
node->left = RRRotate(node->left);
return LLRotate(node);
}
}
else if (factor < -1) //오른쪽으로 치우침
{
if (BalanceFactor(node->right) <= 0) // RR 상태
{
return RRRotate(node);
}
else // RL 상태
{
node->right = LLRotate(node->right);
return RRRotate(node);
}
}
return node;
}
Node* LLRotate(Node* node)
{
Node* newNode= node->left;
node->left = newNode->right;
newNode->right = node;
node->height = 1 + max(Height(node->left), Height(node->right));
newNode->height = 1 + max(Height(newNode->left), Height(newNode->right));
return newNode;
}
Node* RRRotate(Node* node)
{
Node* newNode = node->right;
node->right = newNode->left;
newNode->left = node;
node->height = 1 + max(Height(node->left), Height(node->right));
newNode->height = 1 + max(Height(newNode->left), Height(newNode->right));
return newNode;
}
void Print()
{
InOrder(root);
cout << '\n';
}
void InOrder(Node* node)
{
if (!node) return;
cout << node->data << " ";
InOrder(node->left);
InOrder(node->right);
}
};
int main()
{
AVLTree<int> avl;
avl.Insert(5);
avl.Print();
avl.Insert(6);
avl.Print();
avl.Insert(7);
avl.Print();
avl.Insert(8);
avl.Print();
avl.Insert(9);
avl.Print();
avl.Insert(11);
avl.Print();
return 0;
}
LL 회전과 RR회전이 어떻게 돌아가는지 LR유형을 예를 들어 설명해보겠다
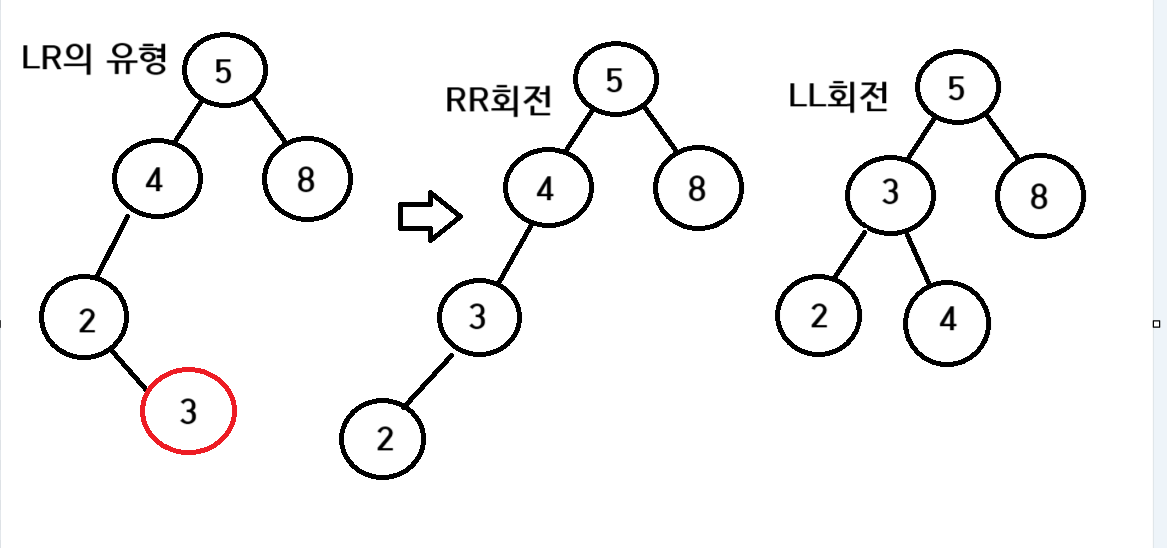
현재 LR 유형이 생겼을때
if (factor > 1) //왼쪽으로 치우침
{
if (BalanceFactor(node->left) >= 0)
{
return LLRotate(node);
}
else // LR 상태
{
node->left = RRRotate(node->left);
return LLRotate(node);
}
}
여기 조건문이 들어가게 된다 node =4가 된다 4인노드와 8인노드의 높이차가 1보다 크게 되었기 때문이다 먼저 node->left =RRRotate(node->left)라고 되어있는데 간단하게 떼었다가 다시 조립을 해준다고 생각하면된다 node->left는 그림에서는 2인노드이다
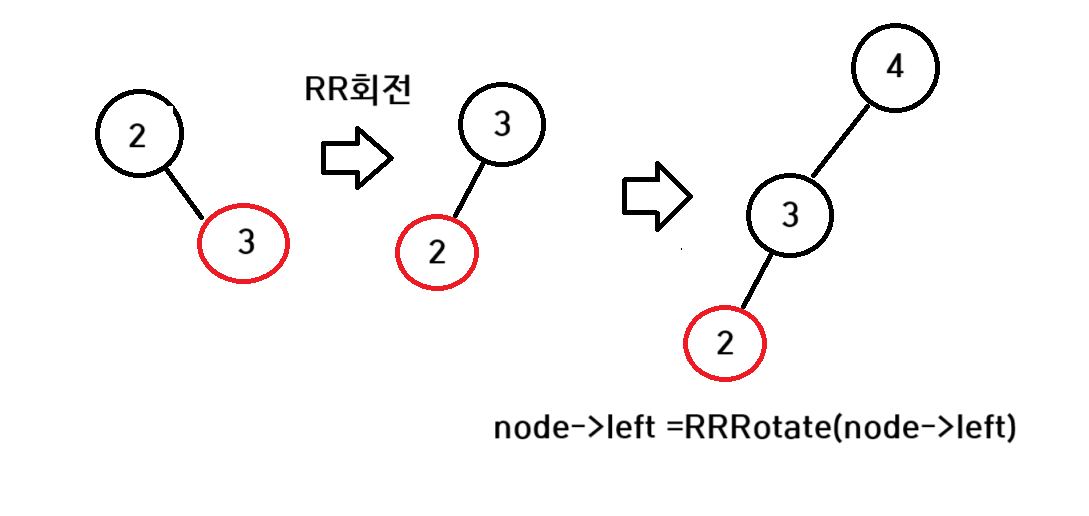
자 이제그러면 LL유형이된다 그다음으로 node를 LLRotate를 돌려준다
node는 그림에서 4인 노드이다
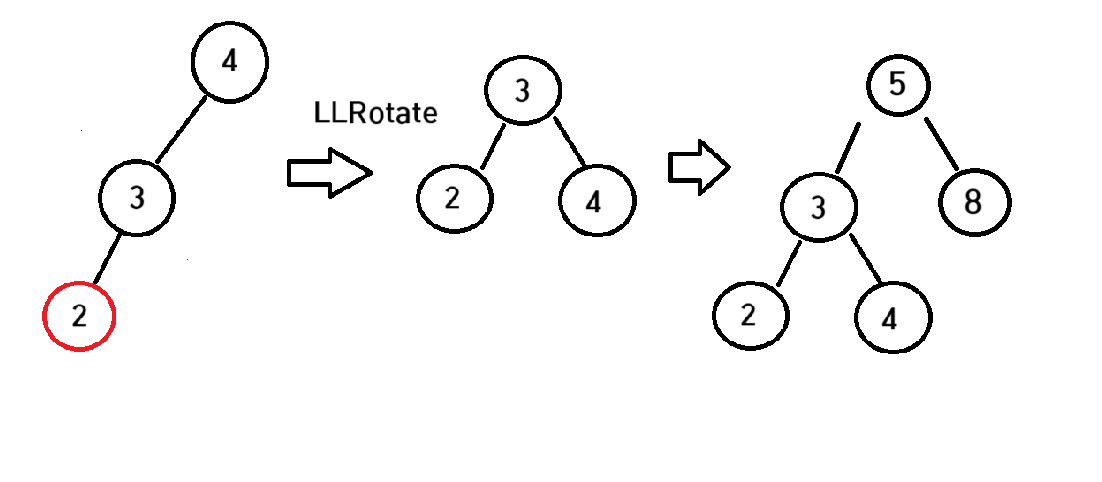
RL유형의 경우 는 LR유형의 반대경우이다 먼저 LLROATE를 돌려 RR유형으로 만든이후 RRroate를 돌려 균형을 맞추어주면된다
이상으로 ..
이렇게 AVL트리를 다루어보았다 아직 삭제는 안다루어보아 글을 안적었지만 이후에는 위 코드에서 삭제 부분까지 다루어보도록하겠다
