이진트리
이진트리는 트리의 모든 노드의 차수를 2이하로 제한을 하여 전체 트리의 차수가 2이하가 되는 트리이다.
이진트리의 모든 노드는 왼쪽 자식의 노드와 오른쪽 자식의 노드만 가진다.
이진트리는 순환적 구성이다.
노드의 왼쪽 자식 노드를 루트로 하는왼쪽 서브트리도 이진트리이다.
노드의 오른쪽 자식 노드를 루트로 하는 오른쪽 서브트리도 이진트리여야한다.
특성
노드가 n개인 이진트리는 루트를 제외한 (n-1)개의 노드가 부모 노드와 연결되는 한개의 간선을 가지기에 n-1개가 된다.
높이가 h인 이진트리가 가질수있는 노드이 개수는 최소 (h+1)개이며 최대
최대(2^(h+1)-1)개 이다.
- 이진트리의 높이가 h가 되려면 한 level 에 최소한 한개의 노드가 있어야 하므로 높이가 h인 이진트리의 최소 노드의 개수는 h+1개 이다.
-하나의 노드는 최대 2개의 자식 노드를 가질수있으므로 레벨 i에서의 노드의 최대 개수는 2^i 개이므로 높이가 h인 이진트리의 전체 노드의 개수는
2^(h+1)-1 개 가 된다.
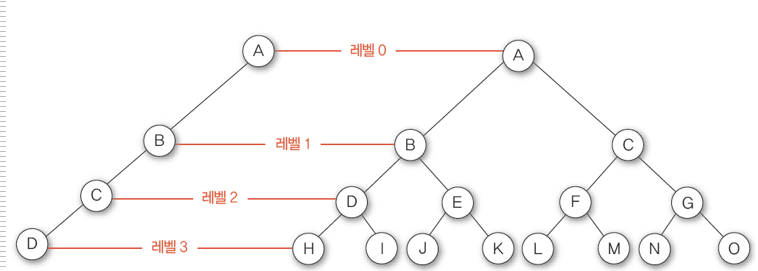
이진 트리 종류
포화 이진트리
포화 이진트리는 모든 레벨에 노드가 포화상태로 차있는 이진트리이다.
높이가 h일때 최대 노드개수인 2^(h+1)-1 의 노드를 가지는 이진트리이며
루트를 1번으로 하여 2^(h+1)-1 까지 정해진 위치에 대한 노드번호를 가진다.
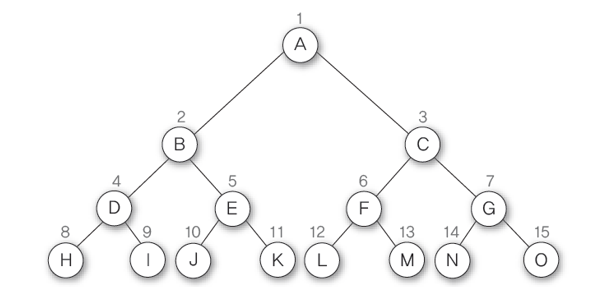
완전 이진트리
완전이진트리는 첫번째로마지막 level 을 제외하고 모든 노드가 채워져야한다. 두번째로는 노드는 왼쪽에서 오른쪽 방향으로 채워져야한다.
첫번째 조건을 보면 마지막 level 을 제외하고 모든노드가 채워져야한다고 하는데 밑의 그림에서 3번 노드를 루트로하는 서브트리가 없다고 가정하자 2번 노드를 생성후 2번 노드의 자식을 생성하게 되면 첫번째 조건인 마지막 level을 제외하였을 때 모든 노드가 채워지지 않았다. 오른쪽 노드가 없기 때문이다. 그렇기에 2번노드를 생성을하고 자식을 생성하기위해서는 3번노드를 우선으로 채우고 자식을 생성시켜주어야한다 .
완전 이진트리에서는 오른쪽 자식노드는 있으나 왼쪽 자식노드가 없으면 이는 완전이진트리 성립하지않는다.
완전 이진트리에서는 왼쪽에서 오른쪽으로 채워져야한다라는 조건에 만족이 되지 않기때문이다.
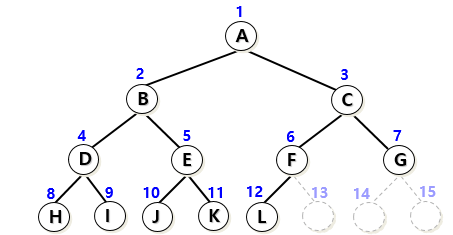
그러나 밑의 그림의 말단 노드를 보면 12번째 노드는 있지만 13번째 노드는 없다. 하지만 이는 완전이진트리를 만족을하게되는데 12번째 노드가 왼쪽에 위치해있어 두번째 조건을 만족하게 됨으로 완전이진트리라고 볼수있다.
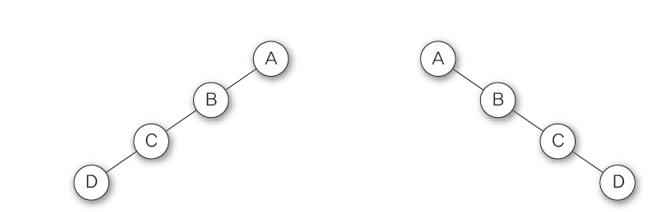
편향 이진트리
높이가 h일때 h+1개의 노드를 가지면서 모든 노드가 왼쪽이나 오른쪽 한방향으로만 서브 트리를 가지고 있는 트리를 편향이진트리라고 한다.
이진트리 구현
#include <iostream>
using namespace std;
template<typename T>
class BinarySearchTree
{
private:
struct Node
{
T data;
Node* left;
Node* right;
};
Node* root;
public:
BinarySearchTree()
{
root = nullptr;
}
Node* CreateNode(T data)
{
Node* newNode = new Node;
newNode->data = data;
newNode->left = nullptr;
newNode->right = nullptr;
return newNode;
}
void Insert(T data)
{
if (root == nullptr)
{
root = CreateNode(data);
}
else
{
Node* currentNode = root;
while (currentNode)
{
if (currentNode->data > data)
{
if (currentNode->left)
{
currentNode = currentNode->left;
}
else
{
currentNode->left = CreateNode(data);
break;
}
}
else if (currentNode->data < data)
{
if (currentNode->right)
{
currentNode = currentNode->right;
}
else
{
currentNode->right = CreateNode(data);
break;
}
}
else
{
cout << "중복 값 허용 x " << '\n';
return;
}
}
}
}
bool IsEmpty()
{
return root == nullptr;
}
void Delete(T data)
{
if (IsEmpty()) return;
Node* currentNode = root;
Node* parent = nullptr;
// 노드 탐색
while (currentNode && currentNode->data != data)
{
parent = currentNode;
if (data < currentNode->data) {
currentNode = currentNode->left;
}
else {
currentNode = currentNode->right;
}
}
if (!currentNode) return; // 삭제할 노드가 없으면 종료
// Case 1: 말단 노드일 경우
if (!currentNode->left && !currentNode->right)
{
if (currentNode == root)
{
root = nullptr;
}
else if (parent->left == currentNode)
{
parent->left = nullptr;
}
else
{
parent->right = nullptr;
}
delete currentNode;
}
else if (!currentNode->left || !currentNode->right)//자식이 하나만 있을경우
{
Node* child = nullptr;
if (currentNode->left)
{
child = currentNode->left;
}
else
{
child = currentNode->right;
}
if (currentNode == root)
{
root = child;
}
else if (parent->left == currentNode)
{
parent->left = child;
}
else
{
parent->right = child;
}
delete currentNode;
}
else //자식이 둘다있을경우
{
Node* childParent = currentNode;
Node* child = currentNode->right;
// 오른쪽 서브트리에서 가장 작은 값 탐색
while (child->left)
{
childParent = child;
child = child->left;
}
if (childParent != currentNode)
{
childParent->left = child->right;
}
else
{
childParent->right = child->right;
}
currentNode->data = child->data;
delete child;
}
}
void InOrder(Node* cur)
{
if (cur == nullptr) return;
InOrder(cur->left);
cout << cur->data << " ";
InOrder(cur->right);
}
void Print()
{
InOrder(root);
cout << '\n';
}
};
int main()
{
BinarySearchTree<int> tree;
tree.Insert(8);
tree.Insert(5);
tree.Insert(7);
tree.Insert(10);
tree.Insert(9);
tree.Insert(4);
tree.Print();
tree.Delete(8);
tree.Print();
tree.Delete(4);
tree.Print();
tree.Delete(7);
tree.Print();
tree.Delete(9);
tree.Print();
tree.Delete(5);
tree.Print();
tree.Delete(10);
tree.Print();
return 0;
}
코드가 굉장히 긴것을 알 수가 있다. 이진 트리구조는 노드를 생성하는 과정은 별로 어렵지않은데 삭제하는 과정이 조금 어렵게 느껴질수가 있다.
말단 노드만 삭제하면 쉽게 가능하지만 문제는 말단 level 이아닌 중간level혹은 루트와 같이 자식 노드가 있는 노드들을 삭제할때를 생각해주어야한다
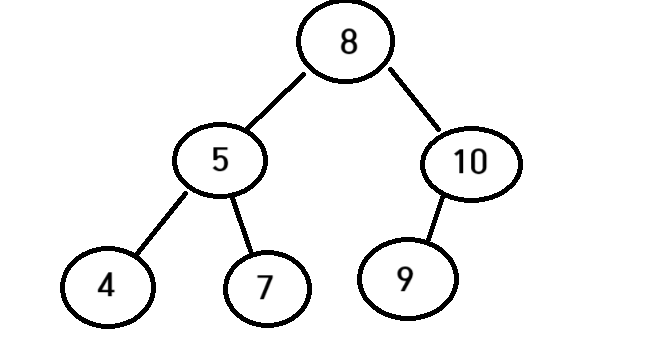
현재 트리가 이렇게 구성되어있다고 생각해보자
나는 여기서 8을 삭제하고싶다
그림에서 보시다시피 8은 현재 루트노드 에 값이 들어가있다 그러면 8을 그냥 삭제해주면 루트가 없어지게된다 그렇기에 8이 삭제되기전 루트 노드를 바꿔줄 필요가있는데 어떠한 값이 그다음 루트가 되어야할까 ?
만약 아무값으로 대체를 하게되면 내가 구성해놓은 트리구조가 무너지게된다
예를 들어 5가 루트가 되면 5보다 큰 7은 5의 왼쪽자식으로 위치가 되어버린다
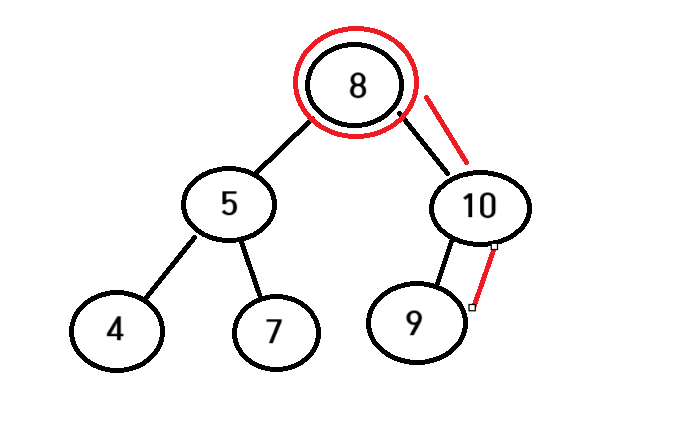
위 코드에서는 부모노드의 값보다 작으면 왼쪽 부모노드의 값보다 크면 오른쪽으로 보내주었다 그렇기에 8을삭제하더라도 문제가 없게 하기위해서는 8 바로 다음으로 큰값을 찾아주어야한다 그렇게 하기위해 8의 오른쪽 자식노드로 들어간다
이후 오른쪽 자식노드에서 왼쪽 자식노드로 계속 들어가주면 루트값보다 바로 큰값이 나온다
그림에서보시다시피 8의 오른쪽 노드인 10으로 들어간다음 10에서 왼쪽 자식노드로 계속 들어가 9를 찾아주게된다
9가 있는 노드를 루트로 바꾸어주고 9가있는노드의 left right 를 루트의 left right 로 넣어준다. 또한 9의 부모노드인 10은 더이상 9를 자식으로 담지 않아야하니 10의 left를 nullptr로 바꾸어 연결을 끊어준다
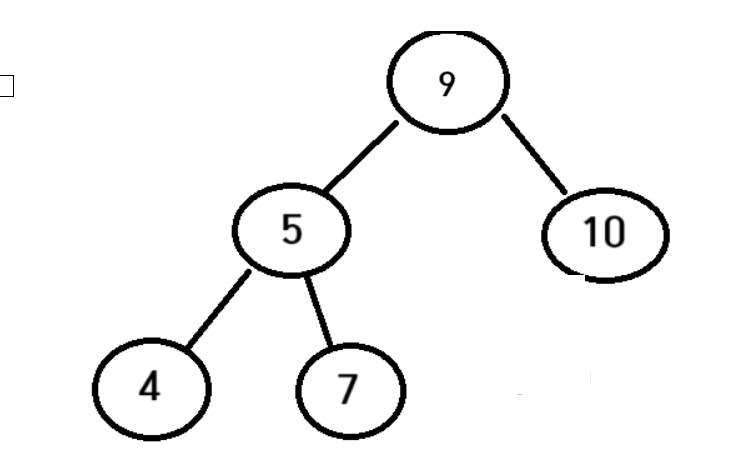
이후 8이삭제가되면 위와 같이 트리가 만들어진다 기존의 트리구조를 무너뜨리지 않고 그대로 유지를 시켜줄수가있다
자식노드가 2개이며 중간level인 노드의 삭제도 생각을해보자
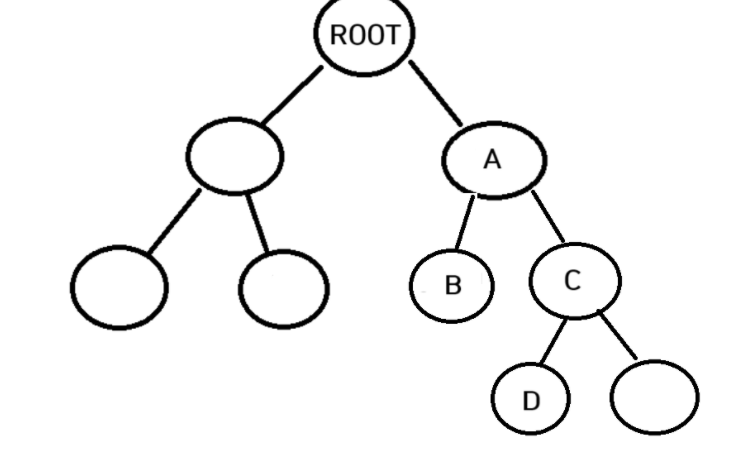
현재나는 A노드를 삭제하고 싶다
A노드의 위치를 대체해줄 노드는 D가 될거다
만약 d에 오른쪽 노드가 있으면 이를 c의 왼쪽 노드에 연결해주고 A 노드의 값을 d노드의 값으로 바꾸어준다 기존 A노드에 d노드의 값을 넣어주었으니 기존의 d값이 들어있던 노드는 삭제시켜준다
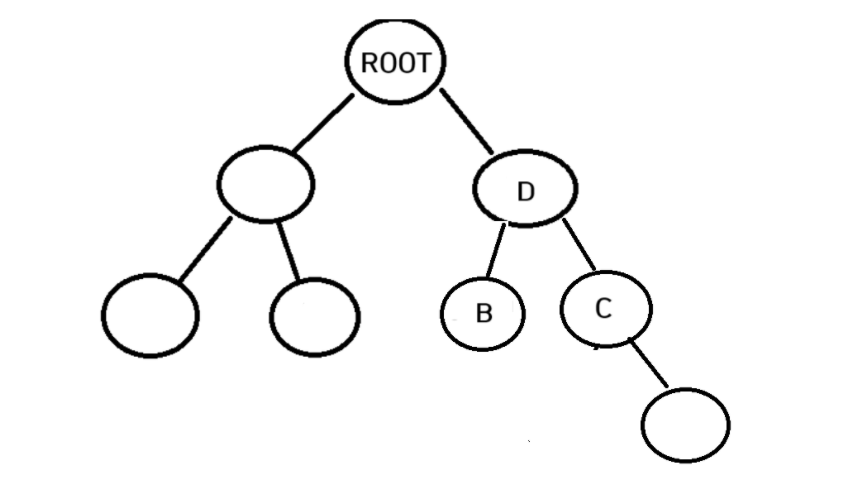
이렇게 트리구조가 완성이된다
만약 나처럼 이 아닌 삭제하고 싶은 A노드를 DELETE를 해주고싶으면 A노드의 부모를 가리키는 포인터를 하나더 추가하여 만들어주면 되게 된다
이상으로..
이렇게 이진트리를 구상해보았다 (코드가 틀렸을수도 있다 이해해주길 바란다 )내가 이번에 구현해놓은 코드는 완전이진트리에서 삭제과정을 거치면 트리의 높이 균형이 깨지게 된다 이를 위한 균형이진트리는 다음에 한번다루어보겠다
