🔍 Problem

1654 랜선자르기

---

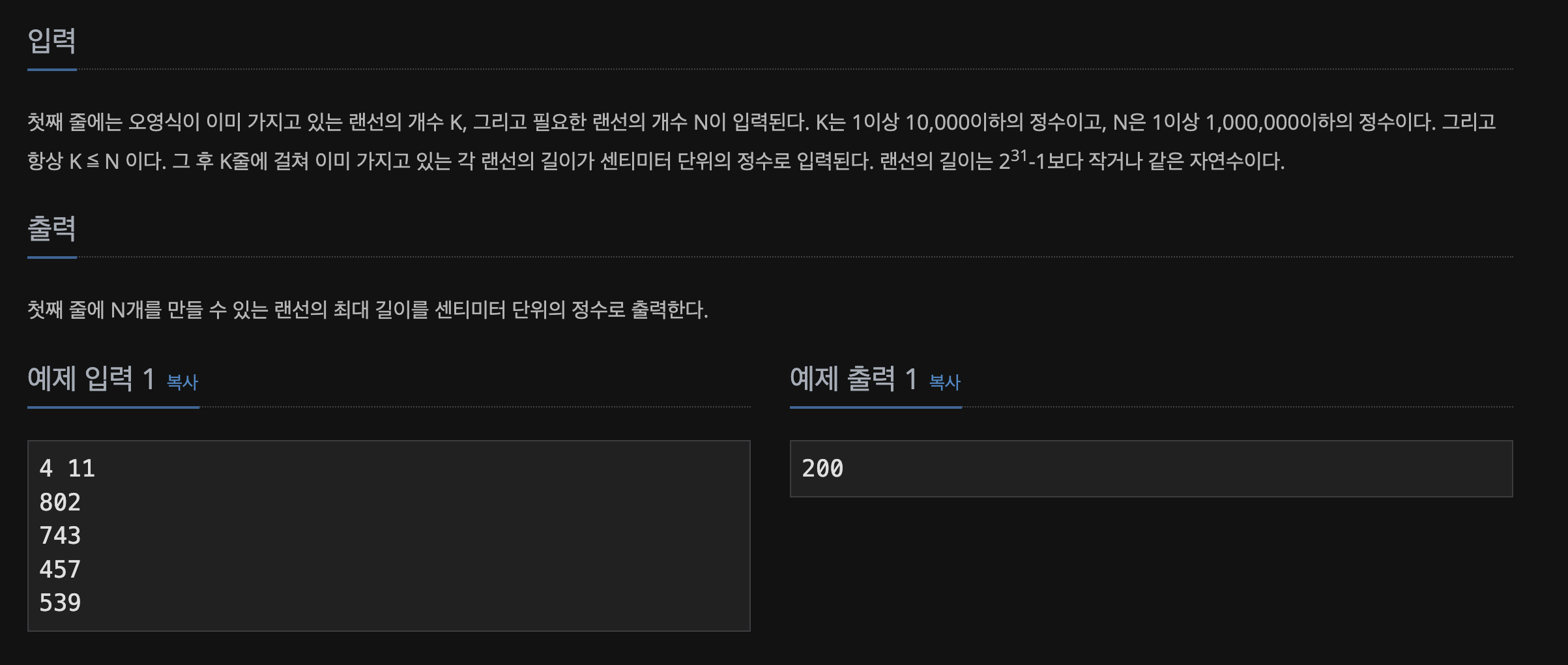
📃 Input&Output

---

🌁 문제 배경

가. 접근 방법
이분탐색을 사용하여 최대로 자를 수 있는 경우를 생각해본다.

나. 사용할 알고리즘 선택

이분탐색

---

📒 해결 과정

가. N을 조정하는 표를 그린다.

랜선의 길이를 이분탐색으로 찾느네 랜섬 길이가 변하는 조건은 아래와 같다.

1. 각 랜선을 일정길이로 나눈 합이 N보다 작으면 자르는 랜선의 길이를 "작게"한다.
2. 각 랜선을 일정 길이로 나눈 합이 N보다 크면 자르는 랜선의 길이를 더 "크게"한다.
3. 만약 같다면(원하는 Nd을 찾았다면), 그래도 혹시 더 큰 랜선길이가 있을 수 있으니까 자르려는 랜선의 길이를 더 "크게"한다.

위의 조건에대로 이분탐색을 한다.

⭐️ 나. 답은 left-1 ?
예제의 풀이 표를 그리다 보면 201에서 계속 left가 고정된다. 이는 만약 N에 맞게 랜선의 길이를 구했어도 N보다 더 큰 숫자의 랜선의 경우를 찾기 때문이다. 따라서 left는 최대값의 다음 값이되고 -1을 해주는 것이다.

right를 출력해도 정답인 이유는 마지막에 left<=right값에 left보다 1 작은 값이 무조건 들어가기 때문이다.

---

💻 Code

import java.util.*;
import java.io.*;

// N개의 랜선 필요
//

public class P1654 {
    public static void main(String args[]) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int K = Integer.parseInt(st.nextToken());
        int N = Integer.parseInt(st.nextToken());

        int[] arr = new int[K];
        for (int i = 0; i < K; i++) {
            arr[i] = Integer.parseInt(br.readLine());
        }

        long right = 0;

        for (int i = 0; i < K; i++) {
            if (right < arr[i]) {
                right = arr[i];
            }
        }

        long left = 1;
        long mid = 0;
        long sum = 0;

        while (left <= right) {
            mid = (left + right) / 2;
            sum = 0;
            for (int i = 0; i < K; i++) {
                sum += (arr[i] / mid);
            }
            if (sum < N) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        System.out.println(left - 1);
        bw.flush();
        bw.close();
    }
}

---

🤔 느낀점

좀 더 풀어보면 익숙해질거 같은 느낌이 든다.