🔍 Problem

11403 경로찾기

---

📃 Input&Output

---

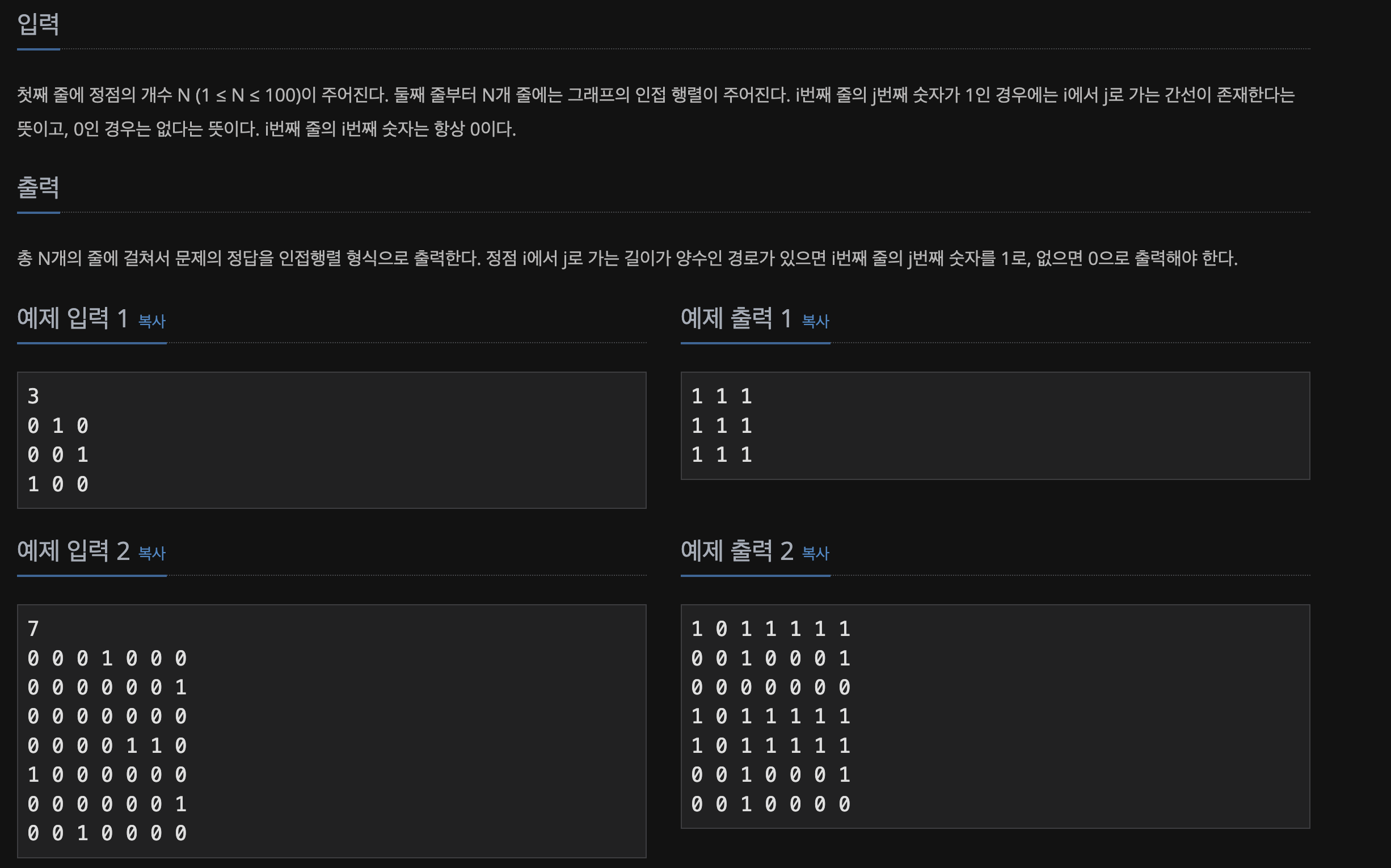
🌁 문제 배경

가. 접근 방법
이 문제는 간선이 주어졌을 때, 이 간선들을 타고 서로의 노드에 결국 도달할 수 있냐를 해결하는 문제이다. 따라서 플로이드워셜 결과가 무한대인 좌표값은 0으로 출력하고 아닌 좌표값은 1로 출력하게 만들면 된다.

나. 사용할 알고리즘 선택
플로이드 워셜

---

📒 해결 과정

가. 플로이드 워셜을 진행한다.

그전에 먼저 0->1의 간선이 존재하는 경우, 1->0도 존재하게 초기 처리를 해놓는다.

플로이드 워셜이란, a->c 이동에서 가운데에 b 노드를 넣어 a->b->c를 이동한다고 가정하는 것부터 시작한다. 이를 dp식으로 생각해보면 그래프가 떠오를 것이고 a->c(a->b->c)를 해결하였으면 a->d도 $a = (a->b->c)->d $으로 치환될 수 있다고 생각할 수 있다.

따라서 결국 모든 정점의 최단거리가 갱신되는 DP식 알고리즘인 것이다.

---

❗ Trouble shooting

가. 자기 자신 이동 불가 문제
그래프 문제의 불문율이 있다. 그것은 바로, 자기 자신은 이동 가능할 수 있다는 것이다. 하지만 이 문제에서는 분물율이 통하지 않는다. 아래의 입력예제 2를 보면 그 상황을 엿볼 수 있다.

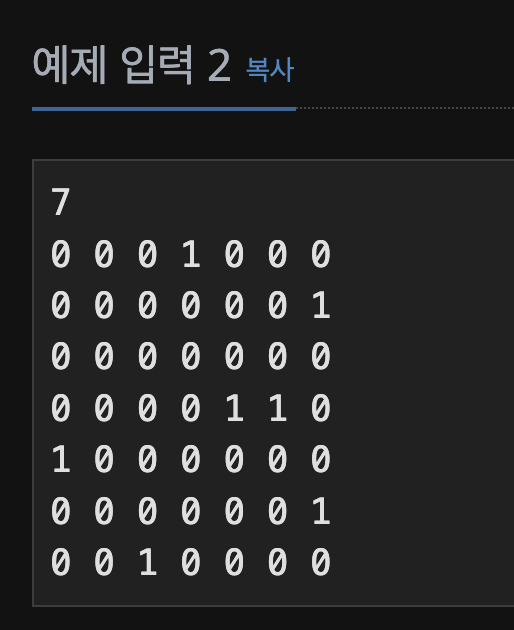
자기자신 즉, i번재에서 i번재 정점으로 간선이 연결되지 않았다->이는 이동할 수 없다.

---

💻 Code

import java.util.*;
import java.io.*;

public class P11403 {
    public static void main(String args[]) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st;

        st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());
        int[][] arr = new int[N][N];
        int tmp;
        int inf = 100000000;

        for (int i = 0; i < arr.length; i++) {
            st = new StringTokenizer(br.readLine());
            for (int j = 0; j < arr.length; j++) {
                tmp = Integer.parseInt(st.nextToken());
                arr[i][j] = tmp;
            }
        }


        for (int i = 0; i < arr.length; i++) {
            for (int j = 0; j < arr.length; j++) {
                tmp = arr[i][j];
                if (tmp == 0) {
                    arr[i][j] = inf;
                }
            }
        }


        for (int n = 0; n < N; n++) {
            for (int i = 0; i < N; i++) {
                for (int j = 0; j < N; j++) {
                    arr[i][j] = Math.min(arr[i][j], arr[i][n] + arr[n][j]);
                }
            }
        }

        for (int i = 0; i < arr.length; i++) {
            for (int j = 0; j < arr.length; j++) {
                if (arr[i][j] == inf) {
                    bw.write(0 + " ");
                } else {
                    bw.write(1 + " ");
                }
            }
            bw.write("\n");
        }
        bw.flush();
        bw.close();
    }

}

---

🤔 느낀점

아주 재밌는 걸 알게되었다.