🔍 Problem

백준 4386 별자리 만들기

---

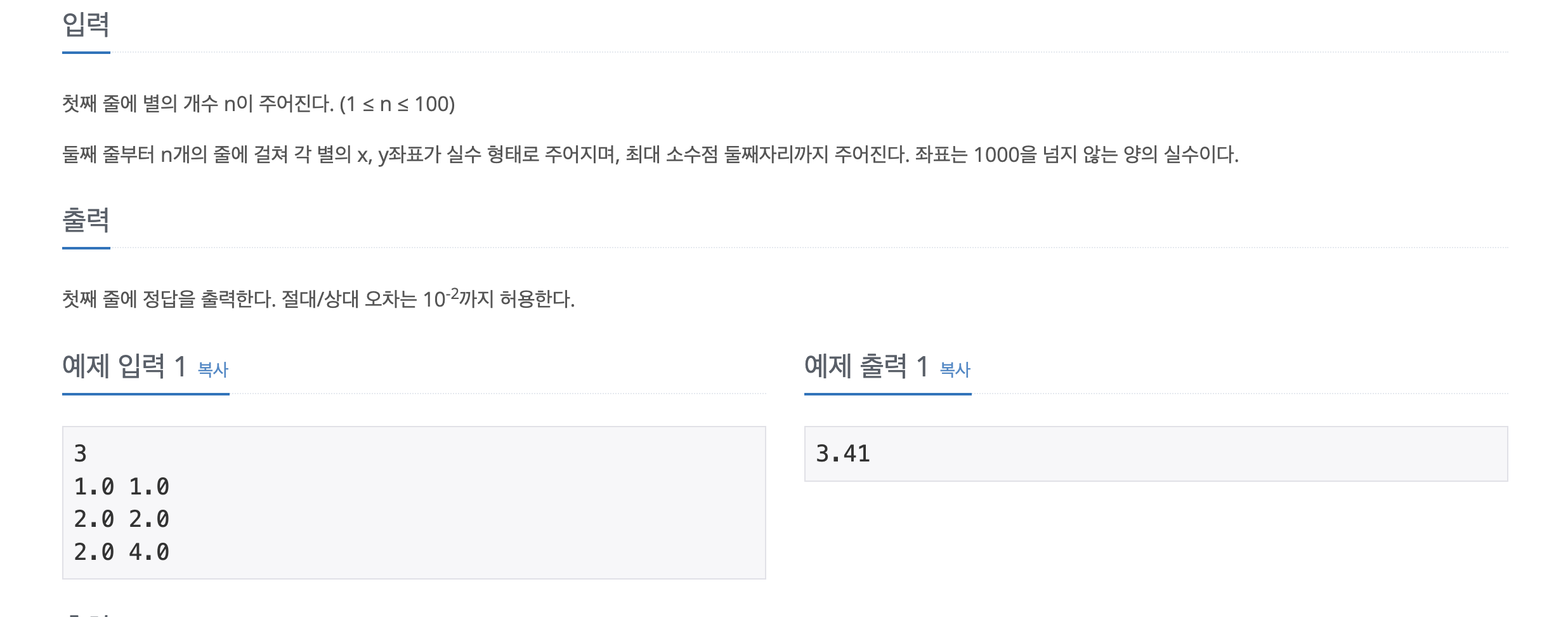
📃 Input&Output

---

🌁 문제 배경

가. 문제 설명
각 별 간에 MST를 구하는 것이다.
MST란?

나. 접근 방법
모든 별이 이어져있다고 하니까 MST 알고리즘을 사용하여 최소 거리 합을 구해주면 된다. 문제는 모든 간선 가중치에 대한 계산을 포함한 간선 정보를 계산하고 모두 우선순위 큐에 넣어야한다는 점이 좀 번거로울 뿐이다.

해당 과정에서 간선을 중복계산하는데 이 때 시간이 x2가 걸리는 것 같다. 최적화의 필요성을 확인하였다.

다. 사용할 알고리즘 선택
MST

---

📒 수도 코드

1. 각 별 사이의 거리를 간선의 가중치로 설정한다.
2. 해당 간선에 대한 정보를 클래스로 만든다.
3. 위에서 만든 모든 간선의 정보를 큐에 넣는다.
4. 큐에서 하나씩 꺼내어 MST를 실행한다.

---

💻 Code

import java.util.*;
import java.io.*;

public class P4386 {

    static class Node {
        public double x;
        public double y;

        Node(double x, double y) {
            this.x = x;
            this.y = y;
        }

    }

    static class Edge implements Comparable<Edge> {
        public int v1;
        public int v2;
        public double weight;

        Edge(int v1, int v2, double weight) {
            this.v1 = v1;
            this.v2 = v2;
            this.weight = weight;
        }

        @Override
        public int compareTo(Edge e) {
            return Double.compare(this.weight, e.weight);
        }

    }

    static double GetDistance(Node a, Node b) {
        return Math.sqrt(Math.pow(Math.abs(a.x - b.x), 2) + Math.pow(Math.abs(a.y - b.y), 2));
    }

    public static void main(String args[]) {
        Scanner sc = new Scanner(System.in);

        int N;
        double x, y;
        double w_sum = 0;
        Node[] node_arr;
        PriorityQueue<Edge> que = new PriorityQueue<>();
        int[] parent;

        N = sc.nextInt();
        node_arr = new Node[N];
        parent = new int[N + 1];

        for (int i = 1; i < N + 1; i++) {
            parent[i] = i;
        }

        for (int i = 0; i < N; i++) {
            x = sc.nextDouble();
            y = sc.nextDouble();

            node_arr[i] = (new Node(x, y));
        }

        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                if (i != j) {
                    Edge e = new Edge(i, j, GetDistance(node_arr[i], node_arr[j]));
                    que.add(e);
                }
            }
        }


        while (!que.isEmpty()) {
            Edge e = que.poll();

            if (find(parent, e.v1) != find(parent, e.v2)) {
                union(parent, e.v1, e.v2);
                w_sum += e.weight;
            }
        }

        System.out.printf("%.2f", w_sum);
    }

    static int find(int[] parent, int v) {
        if (parent[v] == v) {
            return v;
        }
        return parent[v] = find(parent, parent[v]);
    }

    static void union(int[] parent, int v1, int v2) {
        v1 = find(parent, v1);
        v2 = find(parent, v2);

        if (v1 < v2) {
            parent[v2] = v1;
        } else {
            parent[v1] = v2;
        }
    }


}

---

🎸 기타

가. Double.compare(double a, double b)
실수 a와 b를 비교해서 a가 작으면 -1 그리고 b가 작으면 1을 반환한다.

나. Math.sqrt(a,b)
sqrt는 Square(제곱) 와 Root(근)의 문자들을 떼온 것으로 제곱근을 반환한다.

다. Math.pow(a,b)
수학에서 제곱을 "a to the power of b"라고 표현한다. 따라서 power의 앞 세글자를 따와 pow

---

🤔 느낀점

for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                if (i != j) {
                    Edge e = new Edge(i, j, GetDistance(node_arr[i], node_arr[j]));
                    que.add(e);
                }
            }
        }

위의 코드에서 별과 별 사이의 거리를 구할 때, 분명히 중복된 Edge를 생성하였을 것이다. 해당부분에서 시간이 더 걸릴것 같아 이중 for문 순회 부분을 아래 코드로 변경하였다.

for (int i = 0; i < N; i++) {
    for (int j = i + 1; j < N; j++) {
    

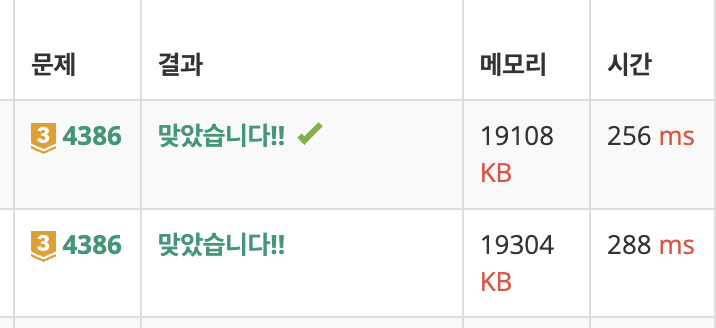
시간을 32ms가량 단축할 수 있었다.