🔍 Problem

백준 1774 우주신과의 교감

---

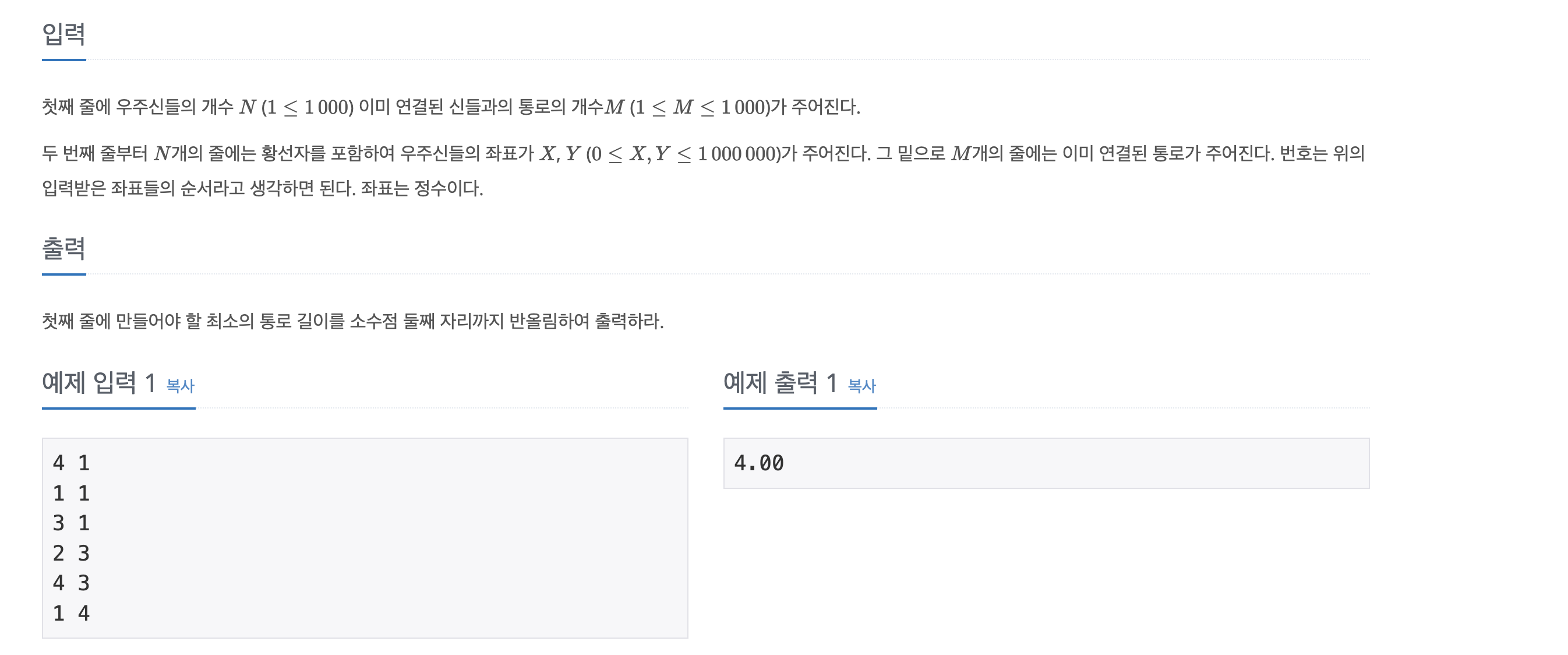
📃 Input&Output

---

🌁 문제 배경

가. 문제 설명
우주신을 노드로 생각한다면, 결국 이 문제는 이미 연결되어있는 간선들을 제외하고 연결할 수 있는 최소 신장 트리(MST)를 만들어 더해진 간선들의 가중치 합을 구하는 문제이다.

나. 접근 방법
이미 연결된 간선은 유니온 파인드의 union을 사용하여 부모(루트)노드가 같게 함으로서 MST를 진행할 때, 예외처리되게 하였다.

다. 사용할 알고리즘 선택
MST

---

📒 수도 코드

1. 좌표를 포함한 노드들을 입력받고 배열에 저장

2. 이미 연결된 노드들은 union연산하여 MST 연산 에서 제외시킨다

3. 각 노드에 대한 간선 클래스(연결된 노드1, 연결된 노드2, 가중치)를 우선순위 큐에 넣는다.

   우선순위 큐를 사용하면 가장 작은 가중치를 가진 간선부터 꺼낼 수 있다. 이를 활용하여 MST구현

4. 큐에서 하나씩 꺼내서, 부모노드가 같지 않은 노드들의 간선을 선택하고 연결시켜 가중치를 더해간다.

---

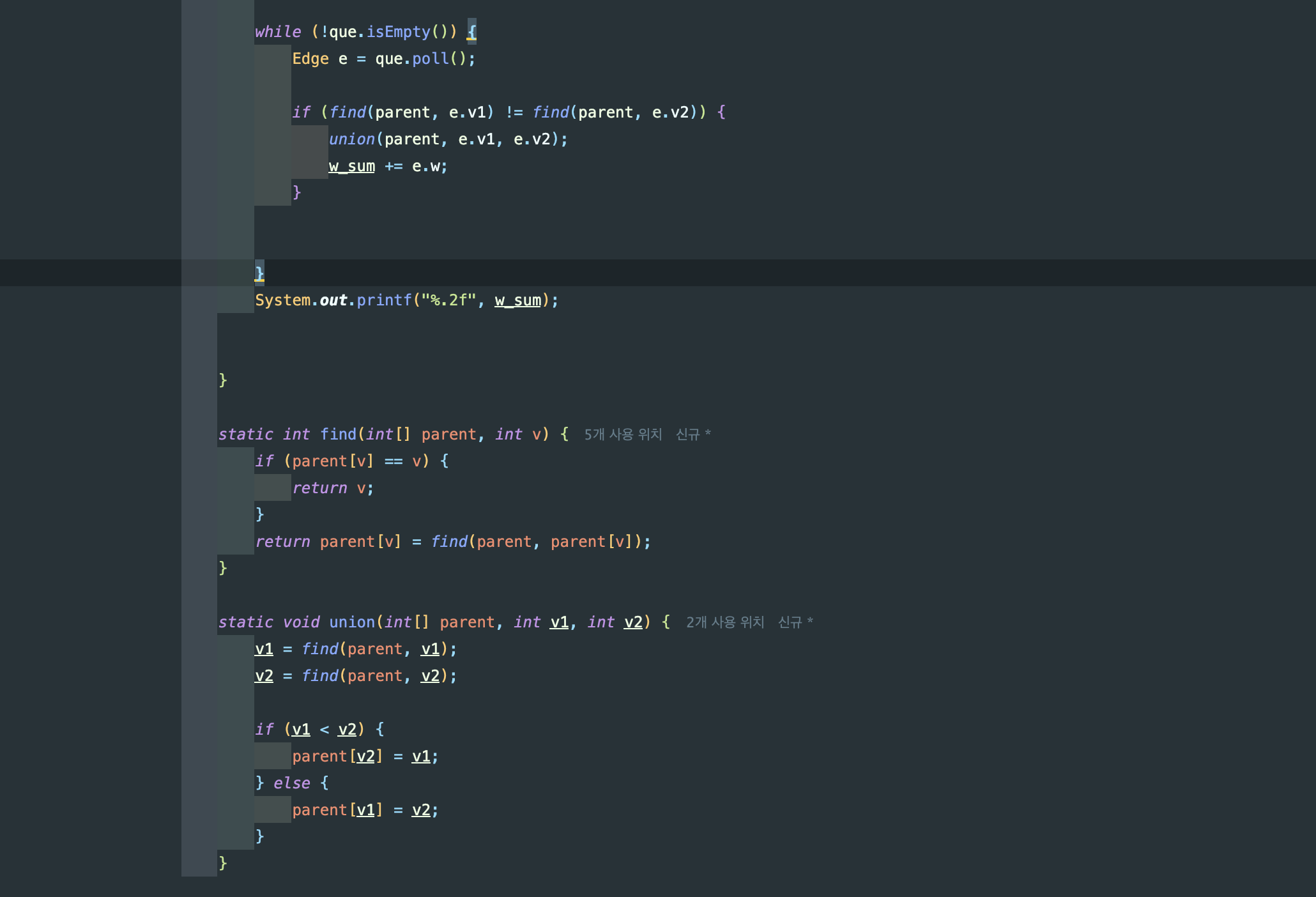
💻 Code

import java.util.*;

public class P1774 {
    static class Edge implements Comparable<Edge> {
        public int v1;
        public int v2;
        public double w;

        Edge(int v1, int v2, double w) {
            this.v1 = v1;
            this.v2 = v2;
            this.w = w;
        }

        public int compareTo(Edge e) {
            return Double.compare(this.w, e.w);
        }
    }

    static class Node {
        public int x;
        public int y;

        Node(int x, int y) {
            this.x = x;
            this.y = y;
        }
    }

    static double getDistance(Node v1, Node v2) {
        int x = v1.x - v2.x;
        int y = v1.y - v2.y;

        double pow_x = Math.pow(x, 2);
        double pow_y = Math.pow(y, 2);

        return Math.sqrt(pow_x + pow_y);
    }

    static public void main(String args[]) {
        Scanner sc = new Scanner(System.in);

        int N, M, X, Y;
        double w_sum = 0;
        int[] parent;
        PriorityQueue<Edge> que = new PriorityQueue<>();
        Node[] nodes;

        N = sc.nextInt();
        M = sc.nextInt();

        nodes = new Node[N + 1];

        parent = new int[N + 1];
        for (int i = 1; i < N + 1; i++) {
            parent[i] = i;
        }

        for (int i = 1; i < N + 1; i++) {
            int x = sc.nextInt();
            int y = sc.nextInt();
            nodes[i] = new Node(x, y);
        }


        for (int i = 0; i < M; i++) {
            int v1 = sc.nextInt();
            int v2 = sc.nextInt();
            union(parent, v1, v2);

        }

        for (int i = 1; i < N + 1; i++) {
            for (int j = 1; j < N + 1; j++) {
                if (i != j) {
                    que.add(new Edge(i, j, getDistance(nodes[i], nodes[j])));
                }
            }
        }

        while (!que.isEmpty()) {
            Edge e = que.poll();

            if (find(parent, e.v1) != find(parent, e.v2)) {
                union(parent, e.v1, e.v2);
                w_sum += e.w;
            }


        }
        System.out.printf("%.2f", w_sum);


    }

    static int find(int[] parent, int v) {
        if (parent[v] == v) {
            return v;
        }
        return parent[v] = find(parent, parent[v]);
    }

    static void union(int[] parent, int v1, int v2) {
        v1 = find(parent, v1);
        v2 = find(parent, v2);

        if (v1 < v2) {
            parent[v2] = v1;
        } else {
            parent[v1] = v2;
        }
    }


}