🔍 Problem

1149 RGB거리

---

📃 Input&Output

---

📒 해결 과정

1️⃣ 결국 최종 비용의 최소값은 바로 이전의 최소값에서 마지막 집의 최소값을 더한 값이다.

위 사진에서 볼 수 있듯이, 모든 집을 색칠하는데 드는 비용에 대한 최소값은 현재 집을 뺀, 바로 이전 집을 색칠하는데 드는 최소 비용의 합과 현재 집을 칠하는데 드는 최소 비용의 합과 같다.

$모든$ $집을$ $색칠하는데$ $든$ $총$ $비용$ = $N-1번째$ $집까지$ $색칠하는데$ $든$ $최소비용$ $+$ $N번째$ $집을$ $색칠하는데$ $든$ $최소비용$

2️⃣ 점화식

가. 개념

"i번째 집까지의 최소비용 = i-1 까지의 최소비용 + i 최소비용"이므로 각 이전의 최선의 값을 구하고 저장해놓는 DP문제인 것이다.

항상 이전의 값이 현재 값에 영향을 미친다는 것을 기억하고 DP로 풀생각까지 이어져야한다.

그렇다면 처음 집부터 최소비용을 구해서 다음 집에 차례로 더해가주면 된다. 그렇다면 $dp[i]+=dp[i-1]$이라는 간단한 식이 되겠지만 그렇지 않다. 조건이 있다.

나. 조건1
그것은 바로, 연속된 집은 같은 색깔로 칠하지 못한다는 것이다. 이것을 해결하는 방법은 다음과 같다.

처음에 R,G 그리고 B 중 어느 색깔을 선택할 것인가?

하지만 DP의 사고방식은 좀 다르게 접근해야한다. 현재 선택이 아니라 다음 선택을 기준으로 이전 선택을 예측해야한다. 이것이 DP식 사고 방식이다. 즉 다시 정리하면

현재 어떤 집을 선택하면 이전 선택에 어떤 영향을 미치는가?

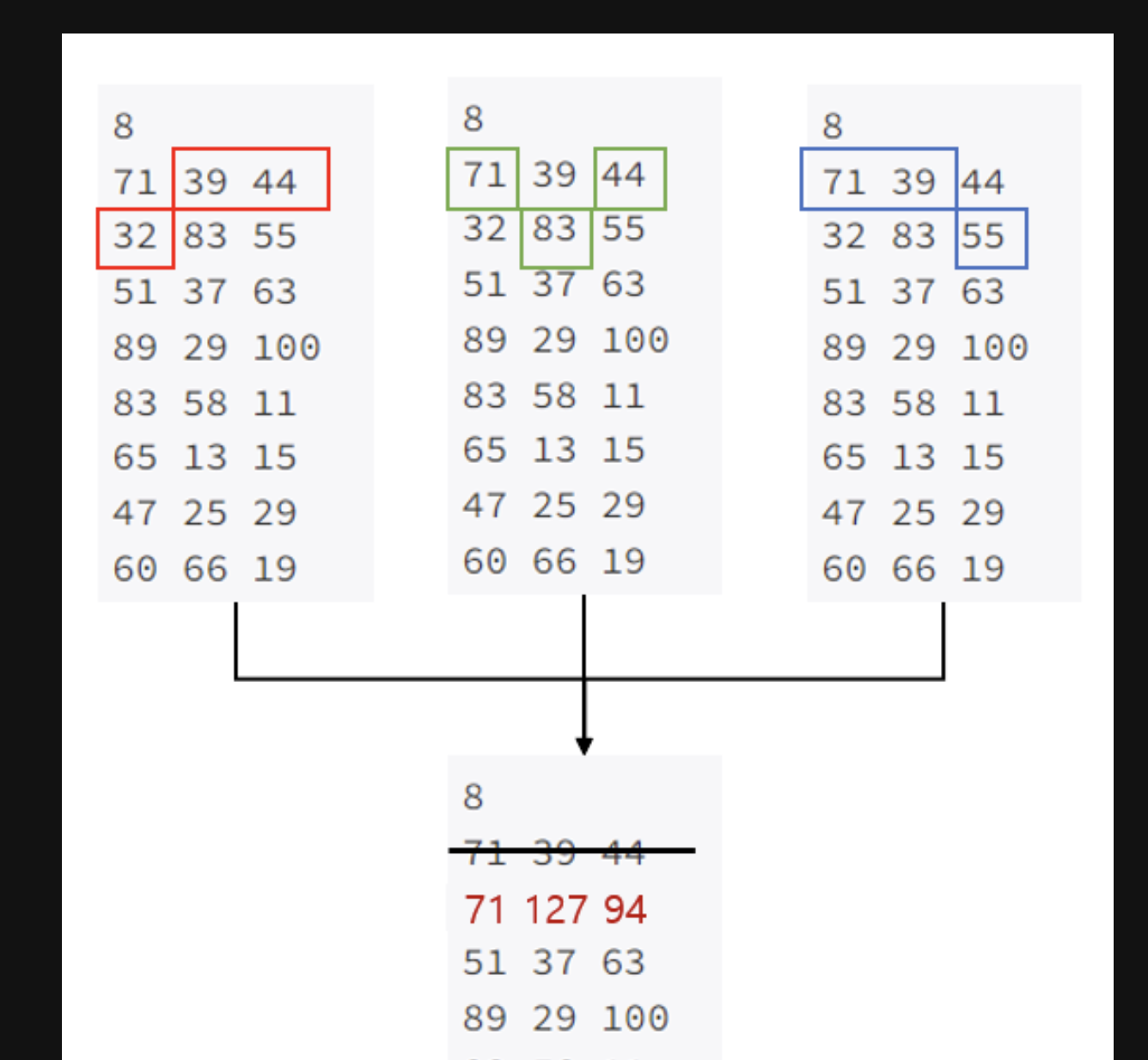
만약 2번째줄 32를 선택한다고 가정하자, 그렇다면 39와 44중 작은 값이 32와 더해져 그 집을 칠하는 최소비용이 될 것이다.

2번째 줄 나머지도 동일하게 계산된다. 쭉 계산하다보면 결국 마지막에 3개의 최소비용이 나올 것이고 그것은 우리가 정했던 방식에 따라 다르게 나올 것이다.(방식 : 2번째 선택에서 어떤 집을 선택했는가.)

다. 점화식 구현
점화식 구현의 케이스는 다음과 같다.
1. 2번째 집의 색깔을 R로 선택했을 때,

$dp[i][0]+=min(dp[i-1][1],dp[i-1][2])$

2. 2번째 집의 색깔을 G로 선택했을 때,

$dp[i][1]+=min(dp[i-1][0],dp[i-1][2])$

3. 2번째 집의 색깔을 B로 선택했을 때,

$dp[i][2]+=min(dp[i-1][0],dp[i-1][1])$

이렇게 각 라인을 구해주면 2차원 DP 매트릭스가 생성된다.

---

💻 Code

// 풀이
// https://velog.io/@halo_3735/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EB%B0%B1%EC%A4%80-1149-RGB-%EA%B1%B0%EB%A6%AC

// const path='input.txt'
const path='/dev/stdin'


const fs = require('fs');

const min = Math.min
// input.txt에서 읽어오기
const input = fs.readFileSync(path, 'utf-8').trim().split('\n');

const N=Number(input[0])
const dp = [[0,0,0], ...input.slice(1).map(line => line.split(' ').map(Number))]

for (let i=1;i<N+1;i++){
    dp[i][0]+=min(dp[i-1][1],dp[i-1][2])
    dp[i][1]+=min(dp[i-1][0],dp[i-1][2])
    dp[i][2]+=min(dp[i-1][0],dp[i-1][1])

}

console.log(min(...dp[N]))

---

🎸 기타

1. 여러개 문자열 입력 2차원 배열로 바꾸기

const a=Array(3)

a[0]="22 21 21"
a[1]="22 21 21"
a[2]="22 21 21"


console.log(a)

const b=a.map(list => list.split(" ").map(Number))

console.log(b) 

>>
  [ '22 21 21', '22 21 21', '22 21 21' ]
[ [ 22, 21, 21 ], [ 22, 21, 21 ], [ 22, 21, 21 ] ]

2. Array.slice(n)
index n부터 반환

a=[1,2,3] 이면
const b = a.slice(1)
b=[2,3]

**3. 2차원 배열 앞에 [0,0,0] 넣기

const dp = [[0,0,0], ...input.slice(1).map(line => line.split(' ').map(Number))]

4. 전개 연산자 (...)

배열의 요소 하나하나를 집어주는(?) 친구이다.
Math.min에 활용가능

console.log(min(...dp[N]))

---

🤔 느낀점

DP식 사고방식이 나는 다음과 같이 해석하였다.

현재 값을 구하는데 이전 값이 "어떤식"으로 영향을 미쳤는가?

이 문제에서는 현재 집의 색깔을 선택한 최소비용이 이전 집들의 최소비용의 합이고 "어떤식"이라는 것은 현재 집의 색깔과 다른 두개의 색깔을 칠하는 최소비용 경우의 수의 최소값이라고 표현하고 싶다.

---

📝 출처

Y_Sevin.log